基于FSA－LSSVR模型的安徽省耕地变化预测

2014-09-06赵艳玲何厅厅刘亚萍石娟娟冉艳艳吴国伟

水土保持研究 2014年3期

赵艳玲，何厅厅，刘亚萍，石娟娟，冉艳艳，倪巍，吴国伟

（中国矿业大学（北京）土地复垦与生态重建研究所，北京100083）

耕地变化预测是土地利用规划中的重要内容之一［1］，可为区域耕地保护政策制定提供重要依据。目前对于耕地变化预测方法的研究较多，有单一方法如回归预测、灰色预测、BP神经网络预测［2－5］等，其中前两种方法是时间序列数据的纯数学处理，缺乏对社会和经济方面变化的综合考虑；BP神经网络易陷入局部最优。也有组合方法如灰色—马儿科夫模型［6］、遗传算法最小二乘支持向量机模型［7］等。前者仍是对时间序列数据的数学处理，后者中的支持向量机（Support Vector Machine，SVM）是基于统计学习理论的VC维理论和结构风险最小化原则的新型学习机器［8］，该方法具有小样本学习、学习效率高与推广性好的特点，能有效避免“过学习”和“维数灾难”等问题，在模式识别［9－10］和回归估计［11－12］等研究领域都取得了很好效果。由于SVM模型最终转化为求解一个二次凸规划问题，当训练数据量大和维数高时，SVM解算速度较慢。Suykens等［13］在标准SVM的目标函数上增加了误差平方和项，提出最小二乘支持向量机回归算法（Least Square Support Vector Machine Regression，LSSVR）。它将线性不等式约束转化为线性等式约束，使得SVM的二次凸规划问题等价于线性方程组求解，极大地提高了SVM的求解效率，也降低了SVM的学习难度［14－16］。将遗传算法与最小二乘支持向量机算法结合，虽然可提高支持向量机模型的预测精度，但是遗传算法同样存在优化过程中容易陷入局部最优的缺陷。

鱼群算法（Fish Swarm Algorithm，FSA）是一种基于动物自治体的优化方法，是集群智能思想的一个具体应用。它能很好地解决非线性函数优化等问题。优化过程中能够很好地跳出局部最优值，并尽可能地搜索到其他的极值，最终搜索到全局极值。将鱼群算法与最小二乘支持向量机回归算法相结合，可避免陷入局部最优，保证了拟合精度，提高了预测能力。

本文以2002—2011年《安徽省统计年鉴》中的数据为依据，构建耕地变化的FSA－LSSVR预测模型，经代入驱动因子数据验证，该模型速度快、精度高，可应用于耕地变化预测。

1 鱼群算法优化最小二乘法支持向量机回归模型

1.1 最小二乘支持向量机回归模型

最小二乘法支持向量机的主要思想是：通过映射函数把输入数据非线性映射到高维特征空间，然后在高维特征空间中解决回归问题P［17］。采用最小二乘支持向量机进行非线性函数估计的算法如下［18－19］：

已知训练样本 D＝｛（x1，y1）│i＝1，2，…，N｝，其中xi∈R″为输入数据，yi∈R是输出类别。在权向量w空间（原始空间）中的最小二乘支持向量机的回归函数问题可以描述为如下问题求解：

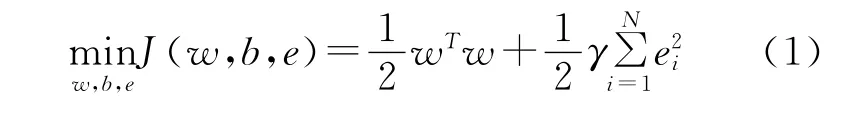
约束条件：yi＝wTφ（xi）＋b＋ei，i＝1，2，…，N其中，φ（xi）：Rn→是核空间映射函数，权向量w∈（原始空间），误差变量ei∈R，b是偏差量。损失函数J是SSE误差和规则化量之和，γ是惩罚因子（常数）。核空间映射函数的目的是从原始空间中抽取特征，将原始空间中的样本映射为高维特征空间中的一个向量，以解决原始空间中线性不可分的问题。

由于w可能为无限维的，于是直接计算规划（1）是极其困难的，因此将这一规划问题转化到其对偶空间中，构建拉格朗日函数：

式中，ai∈R是拉格朗日算子，在LSSVR形式中可以为正，也可以为负。分别对w，b，e，a进行偏微分，可以得到（2）的最优条件，如下：

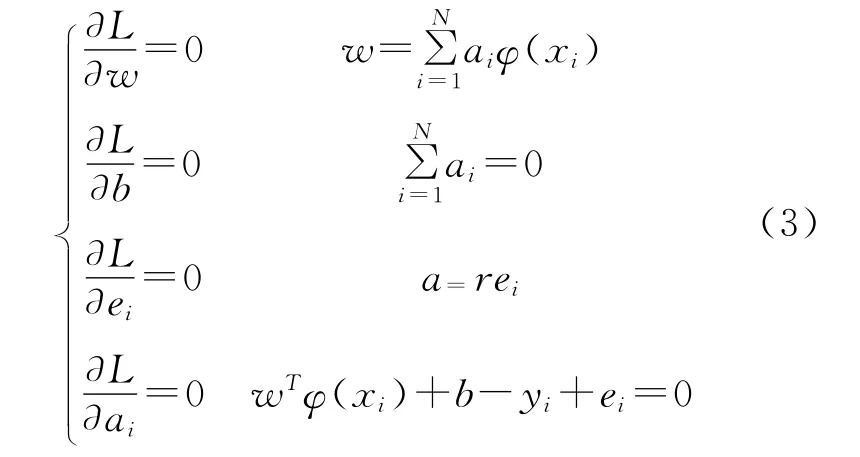
式中，i＝1，2，3，…，N。消除w 和e，得矩阵方程：

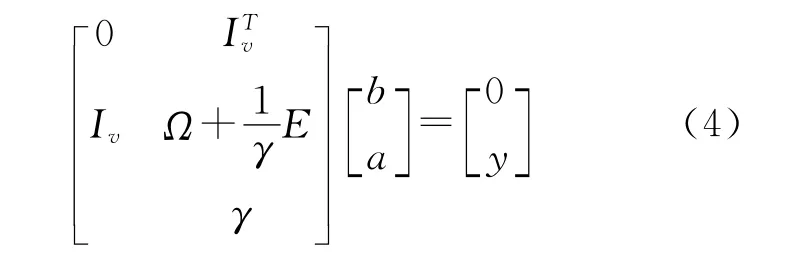
式中，y＝［y1，y2，…，yN］T，I＝［1，…，1］T，a＝［a1，a2，…，aN］T，E是 N×N 维的单位矩阵，Ω＝φ（xi）Tφ（xl），i，l＝1，2，…，N。根据 mercer条件［20］，存在映射函数φ和核函数K（·，·）使得：

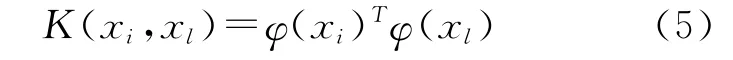
由式（5）进而得到最小二乘法支持向量机回归函数：

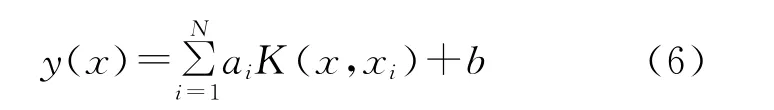
其中a，b由式（4）解得。核函数有多种不同形式，如多项式核函数、高斯核函数、样条核函数、RBF核函数等［21］。在本文耕地变化预测模型中，选择RBF核函数。即K（x，x）＝ilσ为核函数参数（常数）。最小二乘支持向量机回归函数的预测精度和收敛速度受参数（γ，σ）影响，本文选用鱼群算法（FSA）对其进行寻优。

1.2 鱼群算法优化最小二乘支持向量机回归算法参数

鱼群算法（Fish Swarm Algorithm，简称FSA）是一种模拟鱼群运动规律的优化算法，是由李晓磊等［22］在2002年提出的一种新型群体智能优化算法，其基本思想是鱼群向食物浓度较大的水域游动，鱼群规模最大的地方食物浓度最大。据此，鱼群算法构造人工鱼个体，模拟鱼群的觅食、群聚和追尾行为，通过各个体的局部寻优，实现全局最优在鱼群中凸现出来的目的。该算法具有良好的克服局部极值的能力。并且算法中只使用目标函数的函数值，无需目标函数的梯度值等特殊信息，对问题不需要严格的数学机理。对搜索空间具有一定的自适应能力，而且算法对初值没有要求，对各参数的选择也不很敏感［23］。

本文充分利用鱼群算法的全局收敛、初值不敏感、收敛速度快、实时性高等特点［24］，对LSSVR模型的惩罚因子γ和RBF核函数参数σ在设定的范围内进行最优或近似最优参数的选择，以使模型的预测精度获得提高，具体的FSA和LSSVR结合方式如图1所示。

2 基于FSA－LSSVR的耕地变化预测模型的建立

根据已有的研究成果［25－26］，将影响耕地变化的社会经济环境驱动因子划分为自然类（环境变化、自然灾害、气候、地形、地貌等）、人口类（总人口数、农业人口数、第三产业就业人数等）、经济发展类（地区生产总值、第一产业生产总值、人均生产总值、固定资产投资等）、生活水平类（农民人均纯收入、城镇居民消费水平等）及土地政策类（土地管理［27］政策、退耕政策、耕地保护政策等）。从众多的耕地变化驱动因子中选择主要驱动因子是耕地变化预测精度的根本。针对安徽省耕地变化的实际情况，根据定性和定量相结合的办法，依据2002—2011年《安徽省统计年鉴》，应用主成分分析法、相关分析法、迭代回归分析法［28］最终确定影响耕地变化驱动因子指标体系，即第一产业生产总值、农民人均纯收入、农民人口数、第三产业人口数、固定资产投资、城市化水平、耕地保护政策，因变量为耕地面积，具体见表1。其中第一产业总值、农民人均纯收入、农民人口数目、第三产业就业人数、固定资产投资、耕地面积数据直接来源于安徽省统计年鉴，城市化水平通过非农业人数除以人口总数算得，耕地保护政策以数字“1—10”衡量，最严格的耕地保护政策定义为“10”。1998年实施《土地管理法》首次以立法形式确认了“十分珍惜、合理利用土地和切实保护耕地是我国的基本国策”，保护政策为“1”；2004年中央1号文件《中央关于促进农民增加收入若干政策的意见》明确提出“各级政府要切实落实最严格的耕地保护制度”，保护政策为“3”；2005年的《政府工作报告》要求严格保护耕地特别是基本农田，保护政策为“5”；2006年中央1号文件《关于推进社会主义新农村建设的若干意见》在耕地占用税、土地出让金、新增建设用地有偿使用费征缴和使用方面做出了有利于耕地保护的规定，保护政策为“8”；2008年中央《关于推进农村改革发展若干重大问题的决定》提出“坚持最严格的耕地保护政策，层层落实责任，坚决守住1.2亿hm2耕地红线”，保护政策为“10”。

在Matlab R2010环境下，应用SVM和LSSVR工具箱，利用表1中2001—2006年的数据作为训练数据，分别建立多元线性模型、GM（1，1）、BP神经网络、FSA－SVM、FSA－LSSVR 耕地变化预测模型，算得2007—2010年的耕地面积，并与实际耕地面积比较，对各预测模型进行精度评价和验证，具体的耕地预测结果和精度数据见表2、表3和图2。

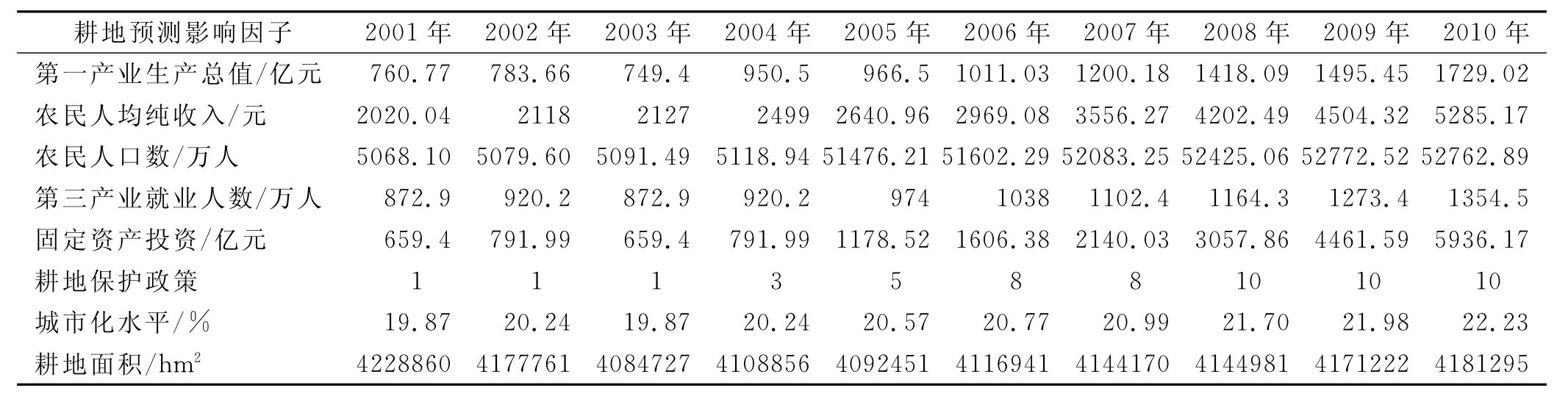
表1 耕地预测影响因子

表2 各模型耕地预测结果

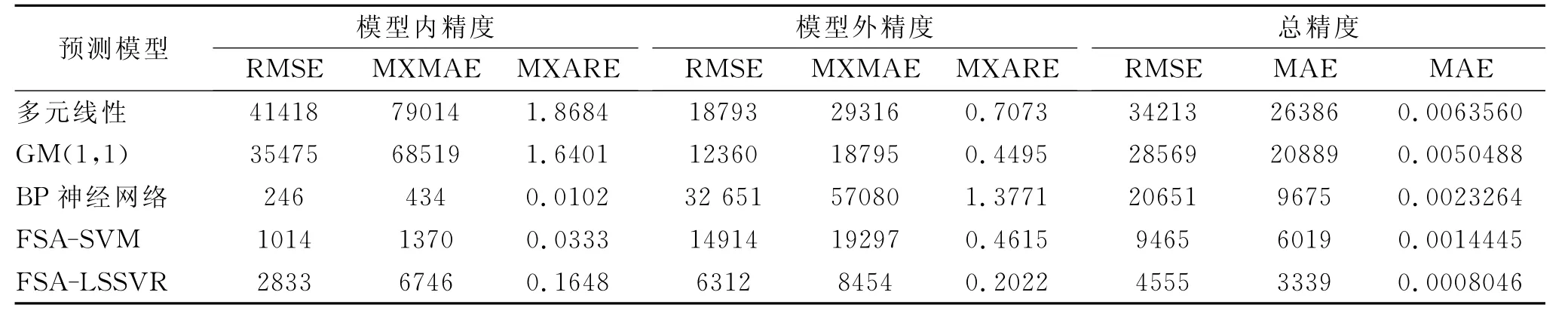
表3 各模型耕地预测精度

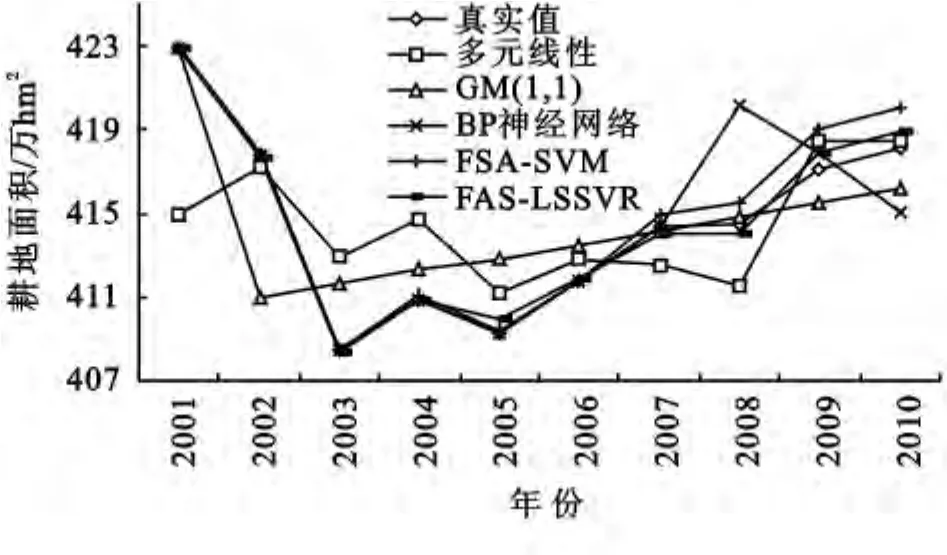
图2 各预测模型耕地预测值和真实值对比

由表2、表3和图2可知：（1）多元线性耕地预测模型的预测精度较差，其模型内和总精度的均方根误差、最大绝对误差、最大相对误差和平均绝对误差在这几种预测模型中最大，表明多元线性模型不能准确表达非线性耕地变化预测；（2）GM（1，1）耕地预测模型仅考虑耕地变化的内在规律，忽略了其他综合因子对耕地变化的外在影响，所以其预测精度不高；（3）BP神经网络耕地变化预测模型的模型内精度最好，各精度指标均优于其它几种预测模型，但其模型外精度指标均低于其他预测模型，且其网络结构复杂，参数确定困难，易产生过拟合现象［24］；（4）FSASVM耕地变化预测模型和FSA－LSSVR耕地变化预测模型的模型外精度和总精度均高于前三个预测模型，模型内精度仅次于BP神经网络耕地预测模型；（5）FSA－LSSVR模型精度略高于FSA－SVM 模型，因为LSSVR模型在标准SVM的目标函数上增加了误差平方和项，把线性不等式约束转化为线性等式约束，求解过程转化为解一组线性方程式，避免了耗时的二次凸规划问题求解，改善了SVM的求解效率，简化了SVM的学习复杂度，提高了模型的预测精度；（6）利用本文引用的安徽省2001—2010年的耕地数据，FSA优化SVM和LSSVR内部参数时，调用SVM 1 500次耗时274.56s，调用LSSVR 1 500次耗时86.37s。可见，FSA－LSSVR的运行速度较快。

3 结论

本文针对耕地变化预测模型的问题，以安徽省耕地变化为例，提出了一种FSA－LSSVR耕地变化预测模型。通过对比分析多元线性、GM（1，1）、BP神经网络、FSA－SVM和FSA－LSSVR模型在耕地变化中的预测能力，得到如下结论：

（1）针对SVM内部参数难以确定的问题，利用FSA的全局搜索能力对惩罚因子γ和RBF核函数参数σ进行最优或近似最优选择，结果证实，FSA能有效地收敛到参数γ和σ的全局最优解。

（2）耕地变化是一种多因素参与的高维非线性预测系统。多元线性模型和单因素GM（1，1）模型均不能准确地表达耕地变化趋势。BP神经网络由于其复杂的网络结构和大量随机的内部参数，使其在耕地变化中的预测精度不高，并且BP神经网络缺乏完善的理论依据。

（3）FSA－LSSVR模型的预测精度指标远高于多元线性、GM（1，1）和BP神经网络模型，且优于FSASVM。

（4）FSA优化SVM和LSSVR内部参数时，调用LSSVR 1 500次较调用SVM 1 500次耗时缩短了近2／3，运行速度大大提高。

总之，FSA－LSSVR模型可以解决SVM内部参数难以确定的问题，适用于多因素参与的高维非线性的耕地变化预测，而且速度快、精度高，具有推广价值。

［1］杜新波，周伟，司慧娟，等.青海省2000—2008年间耕地变化及驱动力研究［J］.水土保持研究，2013，20（5）：180－86.

［2］车明亮，聂宜民，刘登民，等.区域耕地数量变化预测方法的对比研究［J］.中国土地科学，2010，24（5）：13－18.

［3］赵永华，刘晓静，奥勇.陕西省耕地资源变化及耕地压力指数分析与预测［J］.农业工程学报，2013，29（11）：217－223.

［4］赵海英，张明旭.基于灰色模型的耕地变化预测［J］.吉林师范大学学报：自然科学版，2007，5（2）：66－67.

［5］胡喜生，洪伟，吴承祯.基于BP神经网络的福建省耕地预测模型［J］.福建农林大学学报：自然科学版，2008，37（4）：66－67.

［6］黄成毅，邓良基，方从刚.基于灰色—马尔柯夫模型的区域耕地变化预测研究：以四川盆地中部丘陵区为例［J］.四川师范大学学报：自然科学版，2009，32（6）：816－821.

［7］张豪，罗亦泳，张立亭，等.基于遗传算法最小二乘支持向量机的耕地变化预测［J］.农业工程学报，2009，25（7）：226－231.

［8］ Yuan S F，Chu F L.Support vector machines－based fault diagnosis for turbo－pump rotor［J］.Mechanical Systems and Signal Processing，2006，20（4）：939－952.

［9］ Doumpos M，Zopounidis C，Golfinopoulou V.Additive support vector machines for pattern classification［J］.Systems，Man，and Cybernetics，Part B：Cybernetics，IEEE Transactions on，2007，37（3）：540－550.

［10］ Khemchandani R，Chandra S.Twin support vector machines for pattern classification［J］.Pattern Analysis and Machine Intelligence，IEEE Transactions on，2007，29（5）：905－910.

［11］ Wu Z，Li C，Ng J K Y，et al.Location estimation via support vector regression［J］. Mobile Computing，IEEE Transactions on，2007，6（3）：311－321.

［12］ Hao P Y，Chiang J H.Fuzzy regression analysis by support vector learning approach［J］.Fuzzy Systems，IEEE Transactions on，2008，16（2）：428－441.

［13］ Suyken J A K，Vandewalle J.Least squares support vector machine classifiers［J］.Neural Processing Letters，1999，9（3）：293－300.

［14］ Van Gestel T，Suykens J A K，Baesens B，et al.Benchmarking least squares support vector machine classifiers［J］.Machine Learning，2004，54（1）：5－32.

［15］ Anguita D，Boni A.Digital least squares support vector machines［J］.Neural processing Letters，2003，18（1）：65－72.

［16］ Tsujinishi D，Abe S.Fuzzy least squares support vector machines for multiclass problems［J］.Neural Networks，2003，16（5）：785－792.

［17］ Vapnik V N.Statistical learning theory［M］.New York：Wiley，1998.

［18］朱家元，段宝君，张恒喜.新型SVM对时间序列预测研究［J］.计算机科学，2003，30（8）：124－125.

［19］彭珍瑞，孟建军，祝磊，等.基于支持向量机的铁路客运量的预测［J］.辽宁工程技术大学学报，2007，26（2）：269－272.

［20］朱家元，陈开陶，张恒喜.最小二乘支持向量机算法研究［J］.计算机科学，2003，30（7）：157－159.

［21］李波，徐宝松，武金坤，等.基于最小二乘支持向量机的大坝力学参数反演［J］.岩土工程学报，2008，30（11）：1722－1725.

［22］李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式：鱼群算法［J］.系统工程理论与实践，2002，22（11）：32－38.