基于谐波测量的改进余弦窗函数*

莫旭阳,钱承山,王志伟,陶海燕

(南京信息工程大学信息与控制学院,南京 210044)



基于谐波测量的改进余弦窗函数*

莫旭阳,钱承山*,王志伟,陶海燕

(南京信息工程大学信息与控制学院,南京 210044)

摘要:电网电压监测设备在监测运行设备的电流电压波形时通常采用谐波分析法,针对传统FFT谐波分析法在电网频率波动时谐波测量会产生栅栏效应和频谱泄漏的问题,在研究余弦窗特性的基础上提出了一种改进3项余弦窗。通过频谱衰减曲线与传统余弦窗对比,采用基于数据样本的非线性拟合方法,拟合出了改进窗插值算法的谐波幅值相位修正系数,使改进窗插值算法能实际应用于谐波测量。通过谐波测量仿真对比,验证了加改进余弦窗的谐波测量准确度更高。

关键词:谐波测量;FFT分析法;频谱泄漏;余弦窗;加窗插值算法

电网监测设备是保证电网安全稳定运行的重要电子设备,电网监测设备一般通过监测运行设备的谐波电流来判断电网设备的故障和老化。传统谐波测量采用FFT快速傅里叶变换法,在电网频率稳定时谐波幅值和频率测量能满足测量要求。然而电网频率具有时变性,在电网频率波动时,非同步测量会产生栅栏效应和频谱泄漏[1],采用传统傅里叶变换测量谐波会产生较大偏差,降低谐波测量的准确性。

栅栏效应和频谱泄漏主要是由于测量设备的采样频率和电网频率非同步造成的,非同步采样下信号的截取长度与信号周期之比是非整数关系,造成谐波分析傅里叶变换后的频谱线与信号频率不重合从而产生偏差。对采样信号进行加窗插值是目前降低栅栏效应和频谱泄漏的主要方法[2]。传统加窗算法主要采用余弦窗,经典余弦窗有汉宁窗、海明窗、布莱克曼窗以及B-H窗[3]。

本文在研究余弦窗特性的基础上提出了一种基于布莱克曼窗的3项余弦改进窗,该窗较传统余弦窗在旁瓣峰值和旁瓣衰减速度均有提升,通过仿真验证了改进窗的有效性,并通过非线性拟合方法拟合出了改进窗与插值算法结合后的幅值相位修正系数,完善了窗函数,增加了改进窗的实用性。

1　余弦窗函数的特性

余弦窗是定义在[-L/2,L/2]关于X=0轴对称的余弦函数,其在时域中的表达式为:

(1)

对式(1)进行归一化后余弦窗可化为:

(2)

其中

(3)

取窗函数w(t)在t=L/2处的左右极限得:

由函数的连续性和对称性可知,若

(4)

则窗函数在t=±L/2处连续,同时在整个定义域中连续。

对式(2)窗函数w(t)分别求1阶导数、2阶导数后可得:

同理可证明1阶导数w′(t)在t=±L/2处连续,同时在整个定义域中连续。当式(5)成立时,w″(t)在t=±L/2处连续,同时在整个定义域中连续。

(5)

式(3)～式(5)为余弦窗及其1阶2阶导数连续的约束条件[5],其中式(3)为余弦窗的归一化特性。

理想余弦窗应具有较小的旁瓣和较快的旁瓣衰减速度,从而有效抑制信号发生频谱泄漏[6-7]。文献[5]指出余弦窗的旁瓣衰减速度及其最大旁瓣大小与其窗函数及其导数在定义域内的连续性有关。对于2项余弦窗而言,当余弦窗在定义域内连续,即余弦窗系数ak同时满足式(3)和式(4)时,傅里叶变换后的余弦窗旁瓣衰减速度为-18dB/Octave,最大旁瓣为-32dB,特征余弦窗为汉宁窗,2项系数为a0=0.5,a1=0.5,频谱衰减曲线如图1所示。当余弦窗在定义域内不连续,即满足式(3),不满足式(4)时,旁瓣衰减速度降为-6dB/Octave,最大旁瓣减小为-43dB,特征余弦窗为海明窗,2项系数为a0=0.54,a1=0.46,频谱衰减曲线如图2所示。对于3项余弦窗而言,当余弦窗在定义域内连续,二阶导数不连续,即系数ak满足式(3)、式(4)不满足式(5)时,旁瓣衰减速度为-18dB/Octave,最大旁瓣为-58dB。特征窗余弦窗为布莱克曼窗,3项系数为a0=0.42,a1=0.5,a2=0.08,频谱衰减曲线如图3所示。当余弦窗2阶导数在定义域内连续,即系数ak同时满足式(3)～式(5)时,旁瓣衰减速度达到3项余弦窗极大值,平均衰减达到-30dB/Octave,同时最大旁瓣大小达到3项余弦窗极大值,大小为-46dB,特征余弦窗为exact-布莱克曼窗,3项系数为a0=0.375,a1=0.5,a2=0.125,频谱衰减曲线如图4所示。由此推论当3项余弦窗系数满足式(3)、式(4),不满足式(5)时,可以获得较小的旁瓣和较快的旁瓣衰减速度。

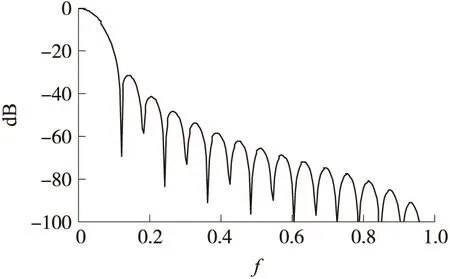
图1　汉宁窗幅频衰减曲线

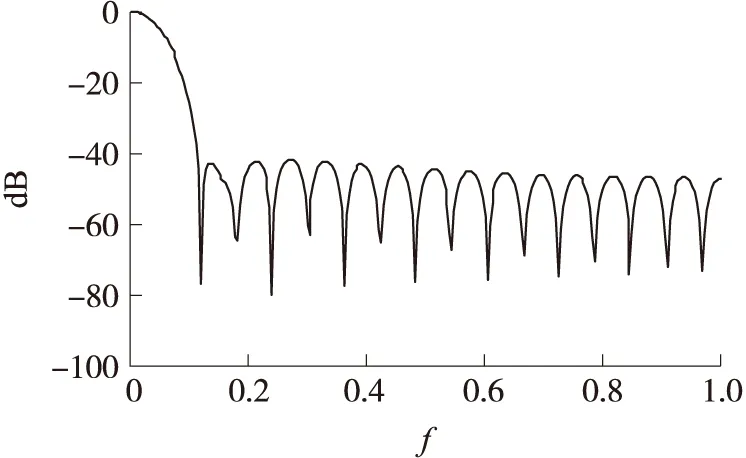
图2　海明窗幅频衰减曲线

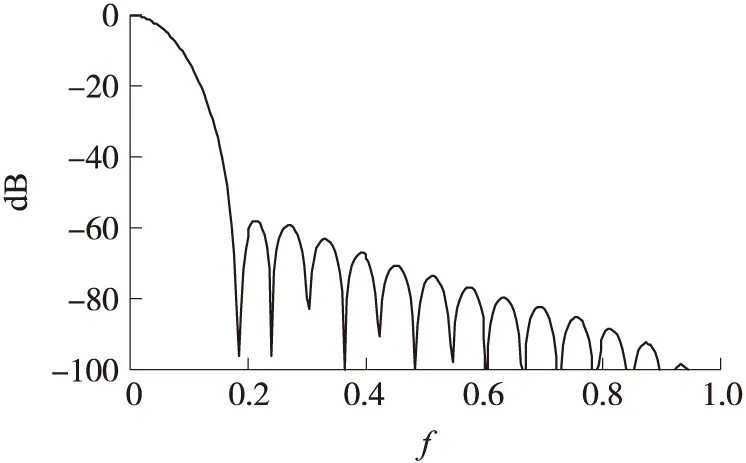
图3　布莱克曼窗幅频衰减曲线

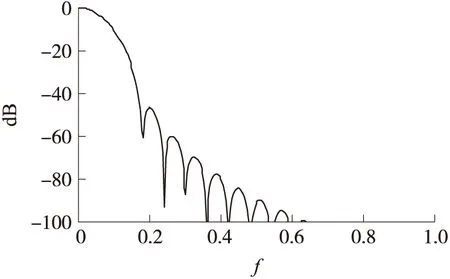
图4　exact布莱德曼窗幅频衰减曲线

2　改进的3项余弦窗函数

2项汉宁窗和3项布莱克曼窗由于窗项数少,计算量小,旁瓣衰减速度快被广泛应用于实际测量中,本文提出了基于3项布莱克曼窗的改进余弦窗,窗函数系数满足前文所述的式(3)、式(4),同时不满足式(5),窗函数时域表达式为:

t≤|L/2|

(6)

其离散表达式和频谱函数分别为式(7)、式(8),其中N为采样点数

n=0,1,…,N-1

(7)

(8)

其中

(9)

为了便于观察改进余弦窗频谱的衰减特性,定义了式(10)的频谱衰减函数,并将频率进行归一化处理

(10)

通过MATLAB软件编程得到改进余弦窗的频谱衰减函数曲线,如图5所示,可以看出改进窗的频谱衰减明显优于其他传统余弦窗,改进窗的最大旁瓣达到-64dB,优于最大旁瓣衰减为-32dB的汉宁窗和最大旁瓣衰减为-58dB的布莱克曼窗;改进窗旁瓣衰减速度为-18dB/Octave,与汉宁窗和布莱克曼窗基本持平。相比窗系数满足式(5)的exact布莱克曼窗,虽然其旁瓣衰减速度达到了-30dB/Octave,但是其最大旁瓣只有-46dB的衰减,远低于-64dB的改进窗,改进窗具有更小的最大旁瓣和较快的旁瓣衰减速度,旁瓣对主瓣影响更小,能更好抑制频谱泄漏。

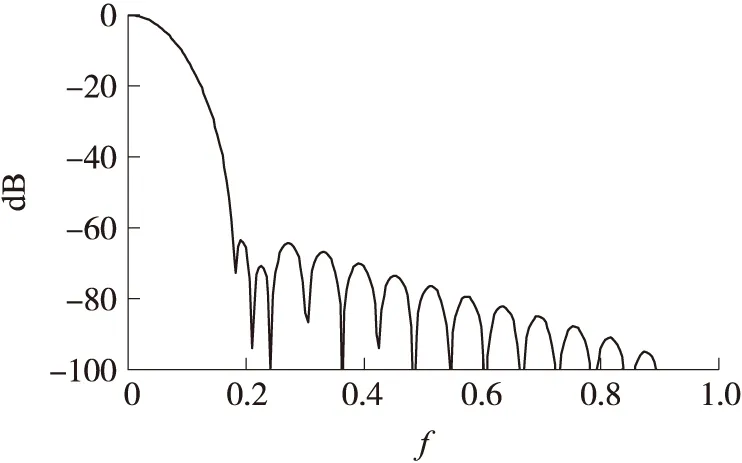
图5　改进窗幅频衰减曲线

3　基于改进余弦窗插值公式修正

由于电网频率具有时变性,实际测量中很难做到同步采样,非同步采样会使得实际谐波频率难以落在频谱线上,使频谱产生栅栏效应,插值算法能通过插值修正减小栅栏效应偏差,还原真实频率,插值算法包括单峰插值和双峰插值[8]。单峰插值算法是搜索最大峰值,双峰插值算法则搜索最大和次大2个峰值。单峰插值易受到频谱泄漏和噪音干扰,本文采用双峰插值对改进的余弦窗进行插值修正。

假设存在一个幅值为A,频率为f0,初始相位为φ待测谐波信号,以fs采样率对其进行采样N点后得到如下离散信号[9]:

(11)

对其所加时域表达式为w(n)的窗函数后进行傅里叶变换得到如下形式的离散信号:

(12)

由于负频点-f0离正频点f0较远,其频峰处的旁瓣影响可以忽略,则正频点f0处的频谱函数表达式为:

(13)

对上式频率进行归一化处理后频谱函数变换为:

(14)

式中λ0是信号频率f0以Δf=fs/N归一化后对应的值,实际测量中信号频率f0很难正好位于频率分辨点上,即f0/Δf不是整数,f0=k0Δf(k0不为整数)。根据双峰插值算法取信号f0对应的频率点k0左右两侧谱线,分别记为第k1和第k2条谱线,显然这两条谱线为k0附近的最大和次大谱线,设两条谱线幅值分别为y1=|Xλ(k1)|和y2=|Xλ(k2)|,k0k1k2满足k1≤k0≤k2=k1+1。

引入辅助参数α[6],令α=k0-k1-0.5,

可推出

f0=k0Δf=(k1+α+0.5)·fs/N

(15)

(16)

(17)

将本文提出的改进窗对应的频谱函数W(n)代入上式可得β关于α的函数,记为β=g(α),其对应反函数记为α=g-1(β)。因为窗函数|W(n)|是偶对称的,所以函数g(α)及其反函数g-1(β)都是奇函数。为了计算方便可将反函数逼近成以下奇次多项式形式:

α=a0β+a3β3+a5β5+a7β7

然而对于3项以上的余弦窗,其对应的函数g(α)很复杂,难以直接获得其对应的反函数g-1(β)。本文采用了基于数据样本的非线性拟合方法,通过MATLAB编程对设定好的谐波信号进行加窗和FFT变换得到变换后的数据样本,所加窗为本文提出的3项改进余弦窗,通过数据样本计算出各次谐波对应的α,β值,再利用MATLAB非线性拟合函数nlinfit()拟合出了奇函数α(β)对应多项式系数,拟合后的α(β)多项式为:

α=1.9β+14.1β3-429.7β5+4191.6β7

双峰插值后信号幅值修正采用了对k1和k2两根谱线的幅值进行加权平均的方法,其幅值修正计算公式为:

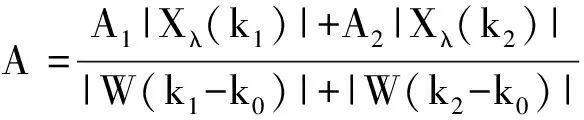
(18)

当采样点数N较大时,式(18)可以进一步化简为:

A=N-1·2(y1+y2)·v(α)

(19)

其中v(α)为偶函数,可以采用多项式逼近偶函数v(α),逼近多项式可表示为:

v(α)=b0+b2α2+b4α4+b6α6

(20)

由于α也为关于β的变量函数,难以直接利用多项式进行函数逼近,同样采用基于数据样本的非线性拟合,通过样本数据进行非线性拟合,拟合后的v(α)函数多项式为:

v(α)=2.7583+1.2513α2-2.3784α4

+8.0707α6

(21)

将式(21)代入式(19)即可得到插值后幅值修正式(21):

A=N-1·2(y1+y2)·(2.7583+1.2513α2

-2.3784α4+8.0707α6)

(22)

插值相位修正公式为式(23):

φ=arg[Xλ(k1)]+π/2-π[α+(-1)i·0.5]

(23)

经过验证拟合后的α值误差为2%左右,属于可以接受的误差范围。本文提出的基于数据样本的方法可适应于其他谐波信号,数据样本采用了所含谐波最高次数为7次的谐波信号,对于其他次数的谐波,修改对应的样本信号函数,通过本文方法可重新拟合出对应系数,便于软件实现。

4　仿真实验

为了验证所提出的改进3项余弦窗,本文通过MATLAB进行仿真研究,信号模拟了7次以内的电网谐波信号。由于我国电网频率波动范围一般为(50±0.5)Hz[10],为了模拟电网频率波动下加窗插值算法的作用,基波频率f1取49.5Hz,采样频率fs为1 600Hz,采样长度为1 024点,基波和各次谐波原始幅值和相位分别如表1和表2所示。

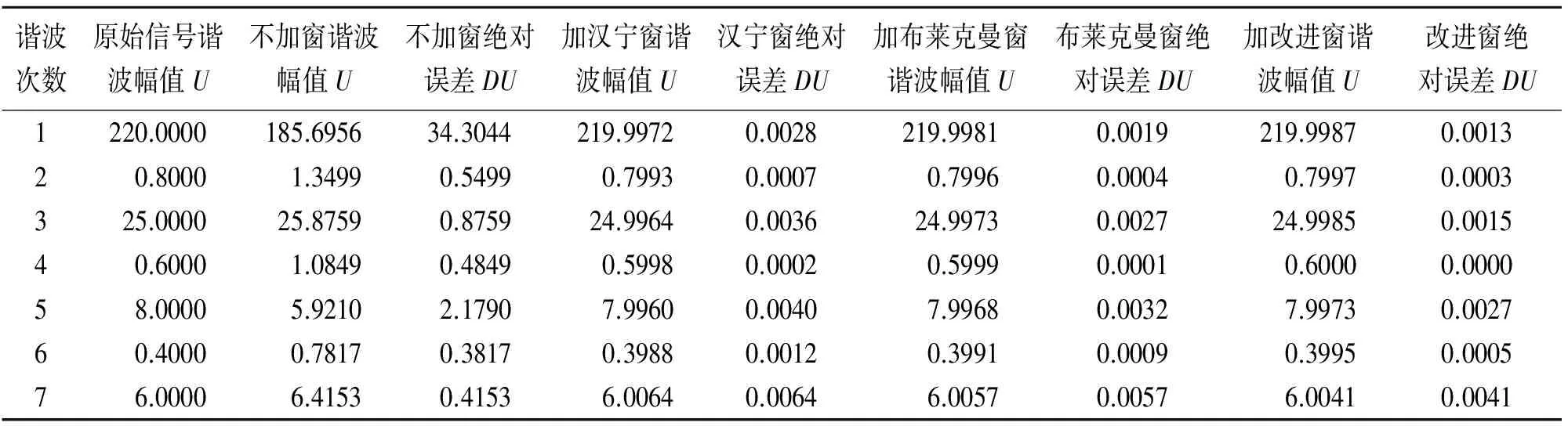
表1　谐波幅值仿真结果对比　单位:V

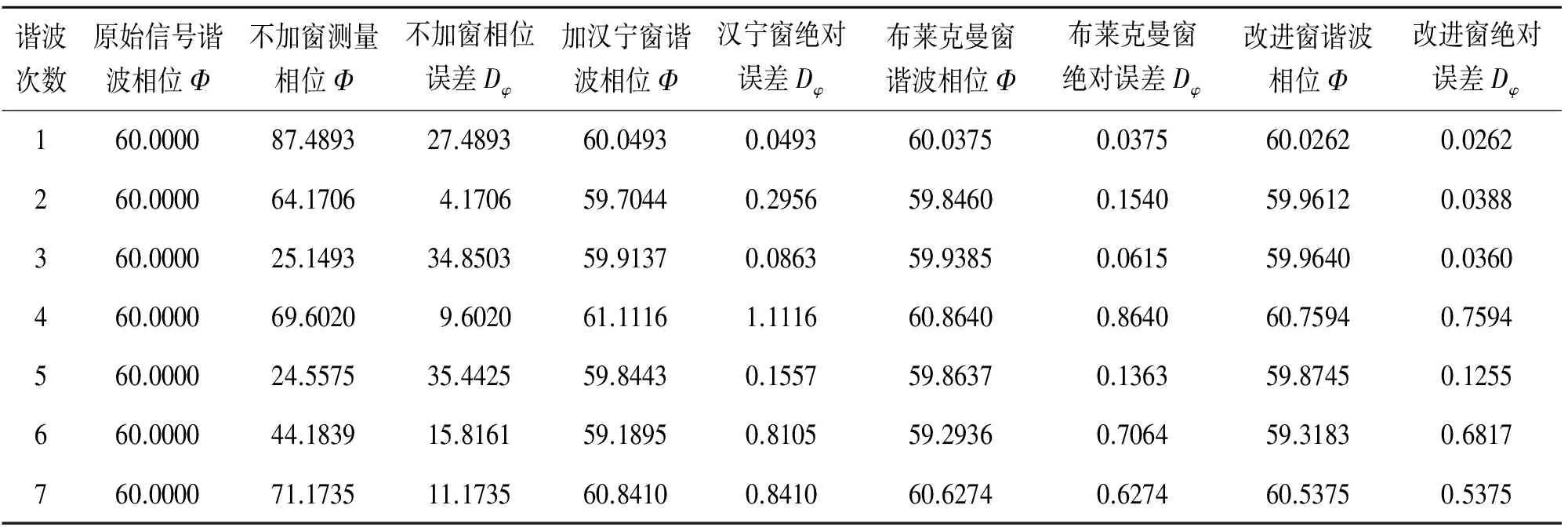
表2　谐波相位仿真结果对比　单位:(°)

仿真过程为先对信号进行采样,对采样后的数据进行加窗处理,然后进行快速傅里叶变换得到频谱数组,通过双峰插值算法,根据幅值和相位的修正式(22)、式(23)进行修正,最后得出修正后谐波的真实幅值和相位,并与传统余弦窗进行了仿真对比,表1和表2分别为不加窗FFT测量、加汉宁窗、布莱克曼窗和改进余弦窗下各次谐波的幅值和相位仿真结果。DU和DΦ分别为测量结果与原始信号幅值和相位的绝对误差。

上述仿真结果可以看出当电网频率发生波动时,传统FFT法存在栅栏效应和频谱泄漏,直接测量谐波会产生很大偏差,所测量的结果无法反应真实谐波信号,采用本文提出的改进余弦窗结合双峰插值算法能有效地减少栅栏效应和频谱泄漏,准确提取谐波信号,对频率波动具有较好的鲁棒性。

5　结论

加窗插值法能有效提高频率波动下谐波测量的准确性,本文提出的改进余弦窗具有更低的旁瓣和旁瓣衰减速度,能有效减小非同步测量带来的栅栏效应和频谱泄漏,结合双峰插值算法可以有效应用于谐波测量中。本文提出的基于数据样本的插值系数拟合方法相比传统求解复杂反函数方法更易实现,稍有不足的是该方法依赖于拟合函数的准确度,若能进一步提高拟合准确度,测量结果将更准确。

参考文献:

[1]林青松,陈清华.谐波检测中频谱泄漏问题的研究[J].工矿自动化,2010(2):53-56.

[2]蒋庆斌,钱金法.继电保护器中的谐波分析[J].电子器件,2012,35(5):562-566.

[3]郭桂香.改进的FFT在电能质量监测系统中的应用[J].自动化与仪器仪表,2011(2):94-95.

[4]许珉,杨阳,章梦哲,等.一种加三项余弦窗的加窗插值FFT算法[J].电力系统保护与控制,2010,38(17):11-14.

[5]Albert H.Nuttall Some Windows with Very Good Sidelobe Behavior[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1981,29(1):84-91.

[6]Qian Hao,Zhao Rongxiang,Chen Tong.Inter-Harmonics Analysis Based on Interpolating Windowed FFT Algorithm[J].IEEE Transactions on Power Delivery,2007,22(2):1064-1069.

[7]熊杰锋,王柏林,孙艳.电力系统间谐波和谐波分析的海宁窗插值算法[J].自动化仪表,2010,31(4):25-27.

[8]王巍,陈慧慧,刘伟伟,等.基于二阶海宁卷积窗和双峰插值傅里叶变换的谐波检测方法[J].工矿自动化,2010(10):49-52.

[9]牛胜锁,梁志瑞,张建华.基于三谱线插值FFT的电力谐波分析算法[J].中国电机工程学报,2012,32(16):130-135.

[10]杨拴科,何卫锋.非同步采样对电力系统谐波分析精度影响的仿真研究[J].电工技术杂志,2003(5):36-38.

莫旭阳(1988-),男,汉族,江苏苏州人,南京信息工程大学信息与控制学院硕士研究生,主要研究方向为避雷器在线监测、嵌入式系统、物联网应用,moxuyang163@163.com;

钱承山(1971-),男,汉族,山东泰安人,南京信息工程大学信息与控制学院教授,博士,硕士生导师,主要研究方向为非线性系统控制、自动检测技术、智能终端与物联网应用等,qianchengshan@163.com。

ImprovedCosineWindowFunctionBasedonHamonicMeasure*

MOXuyang,QIANChenshan*,WANGZhiwei,TAOHaiyan

(School of Information and Control,Nanjing University of Information Science and Technology,Nanjing 210044,China)

Abstract:Grid voltage monitoring equipments in the monitoring current and voltage waveforms of operating equipment commonly use the method of harmonic analysis.To solve the problem that traditional FFT harmonic analytical algorithm produces fence effect and spectrum leakage when the grid frequency shifts,an improved method of three cosine windows is proposed on the characteristic research of cosine window.Comparison to traditional windows through the spectrum attenuation curve shows superiority,a nonlinear fitting method based on the data sample is used to calculate correction factors for harmonic amplitude and frequency of the improved cosine window interpolated algorithm.With the corrected factors,the improved algorithm can be applied to real harmonic measure.Contrast to harmonic simulation results,the improved cosine window shows higher accuracy.

Key words:harmonic measure;FFT analytical algorithm;spectrum leakage;cosine window;windowed interpolation algorithm

doi:EEACC:815010.3969/j.issn.1005-9490.2014.04.042

中图分类号:TM714

文献标识码:A

文章编号:1005-9490(2014)04-0777-05

收稿日期:2013-04-09修改日期:2013-12-28

项目来源:企事业委托项目(2013h066);南京信息工程大学科研启动基金项目(20100307)