三向力传感器标定的计算

席本强,何 毅

(辽宁工程技术大学机械工程学院,辽宁 阜新 123000)



三向力传感器标定的计算

席本强*,何 毅

(辽宁工程技术大学机械工程学院,辽宁 阜新 123000)

从抽象的三输入三输出数学模型出发,建立三向力传感器的一般数学模型,对该模型进行一阶泰勒展开并将拉格朗日余项作为误差忽略,得到三向力传感器线性标定计算的正则方程组。分别在3个方向采取单向多次加载,通过最小二乘法将输出与载荷对应的数据进行线性拟合,将拟合结果与原正则方程组比对,确定其系数阵,从而得出标定的算法。该标定方法推导中仅假定传感器3个应变梁正交,同时考虑了三向变形耦合关系,而没有限定传感器的具体结构形式,因而该算法对于不同结构的三向力传感器具有一定的通用性。该算法为多向耦合类型传感器的标定提供了新的思路和研究方法。

三向力传感器;算法;标定;模型;系数阵

三向力传感器的标定工作一直是工程测试中的重要环节[1],传感器的标定是保证试验台正常工作和准确测量的关键,标定的结果直接影响测试结果的精度及可靠性[2]。因此,通常为了保证传感器测量值的准确传递,需要在其制造、装配完毕后,以及经过使用或维修后必须对其设计指标进行标定实验,使其性能达到指标要求[3-4]。

三向力传感器的标定方法是通过实验将已知的被测量输入待标定的三向力传感器而得到传感器的输出量,将采集到的传感器输入量和输出量进行处理、比较,得到输入输出对应关系的标定曲线,最终得出传感器性能指标的实测结果[5-6]。目前对其输入输出量进行处理而得到其标定曲线的方法有直线拟合、二次抛物线拟合、插值法等,但都具有计算误差较大、计算限制条件多等缺点,不能广泛使用[7]。

计算三向力传感器标定的算法大都只考虑单方向的变形,并没有考虑三向变形耦合关系。由于变形协调原因,每个单向加载在3个变形梁上都会有应变输出,因而造成了对三向力传感器的标定不够准确[8],在三向力传感器的实际应用中就难以会出现不必要的损失。为了准确得到三向力传感器的标定,本文从数学模型的建立开始进行研究,采用精确度高的最小二乘法对数据进行拟合,从不同的角度出发得到了三向力传感器标定的算法。该算法可以计算3个方向的标定,为今后数据处理方法提供了很好的借鉴。

1 三向力传感器标定算法的数学模型

传感器的3个应变梁正交分布[9],在空间力作用下发生应变。由于在某一方向作用的力,其变形不只在一个方向发生,另外2个方向也会发生应变[10],所以三向力传感器不能仅视作3个单项力传感器。而应该综合考虑其变形协调作用,各方向作用力的耦合作用。

设一个三向力传感器在受力(载荷)F的作用下,在直角坐标系下,F在三坐标轴的3个分力则分别为Fx、Fy、Fz,假设这3个分力的大小分别为X、Y、Z,则力F可用向量{X,Y,Z}T表示。

传感器在三坐标上相应的应变εx、εy、εz经应变桥电路处理后的输出信号分别为Ux、Uy、Uz,则此3个输出信号一定是输入量F={X,Y,Z}T的函数[11-12],即

(1)

方程组(1)的定义域为三向力传感器的量程,记为Ω,则∀F∈Ω在Ω内连续且可导。

设某次测量时所加载荷为F0={X0,Y0,Z0}T,传感器的信号输入为U0={Ux0,Uy0,Uz0}T,则对方程组(1)中的Ux在F0点泰勒展开,可得,

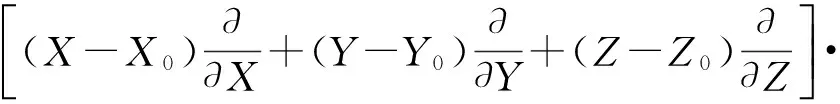
(2)

其中R(ξ,ζ,ψ)为拉格朗日余项,此处作为系统误差略去[13]。则式(2)可以简化为

Ux=fx(X0,Y0,Z0)·X+fy(X0,Y0,Z0)·Y+
fz(X0,Y0,Z0)·Z+
[Ux0-X0fx(X0,Y0,Z0)-Y0fy(X0,Y0,Z0)-
Z0fz(X0,Y0,Z0)]

(3)

对三向力传感器,在其量程范围内,一般都在线性弹性内[14],且3个分力正交、独立作用,则

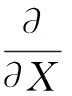
(4)

其中a1、b1、c1为常数,由传感器系统刚度决定。由式(4)可得

fx(X0,Y0,Z0)=fx(X0)=a1
fy(X0,Y0,Z0)=fy(Y0)=b1
fz(X0,Y0,Z0)=fz(Z0)=c1

(5)

将式(5)代入式(3)可得

Ux=fx(X0)·X+fy(Y0)·Y+fz(Z0)·Z+
[Ux0-X0fx(X0)-Y0fy(Y0)-Z0fz(Z0)]=
a1X+b1Y+c1Z+Ux0-a1X0-b1Y0-c1Z0

(6)

同理可得

Uy=gx(X0)·X+gy(Y0)·Y+gz(Z0)·Z+
[Uy0-X0gx(X0)-Y0gy(Y0)-Z0gz(Z0)]=
a2X+b2Y+c2Z+Uy0-a2X0-b2Y0-c2Z0

(7)

Uz=hx(X0)·X+hy(Y0)·Y+hz(Z0)·Z+
[Uz0-X0hx(X0)-Y0hy(Y0)-Z0hz(Z0)]=
a3X+b3Y+c3Z+Uz0-a3X0-b3Y0-c3Z0

(8)

2 算法求解

对传感器标定时,一般采用单向分别加载:

①对X方向单向加载时,则有Fx0={X0,0,0}T,而输出信号则是3个通道都有,即Ux0={Uxx0,Uyx0,Uzx0}T。则有

Uxx=a1X+Uxx0-a1X0
Uyx=a2X+Uyx0-a2X0
Uzx=a3X+Uzx0-a3X0

(9)

在X0点附近进行多次标定,得

{X1,0,0}T→{Uxx1,Uyx1,Uzx1}T,
{X2,0,0}T→{Uxx2,Uyx2,Uzx2}T,
…

将所测Xi,i=1,…,N,Uxxi,i=1,…,N进行线性拟合,得直线

(10a)

同理可得:

(10b)

(10c)

忽略传感器初值误差,必有F0=0时[15-16],U0=0,则此时

Uxx0-a1X0=Uyx0-a2X0=Uzx0-a3X0=0

而式10(a)～式10(c)中,D1、D2、D3三者的理论值都应为零,这里忽略标定测量中产生的非齐次测量。因此,比较式(9)和式10(a)～式10(c)可得

a1=A1,a2=A2,a3=A3

②同理对Y方向单向加载,则有Fy0={0,Y0,0}T,输出信号Uy0={Uxy0,Uyy0,Uzy0}T。则有

Uxy=b1Y+Uxy0-b1Y0
Uyy=b2Y+Uyy0-b2Y0
Uzy=b3Y+Uzy0-b3Y0

(11)

在Y0点附近进行多次标定,得

{0,Y1,0}T→{Uxy1,Uyy1,Uzy1}T
{0,Y2,0}T→{Uxy2,Uyy2,Uzy2}T
…

将所测Yi,i=1,…,N,Uxyi,i=1,…,N进行线性拟合,得直线

(12a)

同理可得:

(12b)

(12c)

如果三向力传感器采用压电晶桥或全桥应变测量,必有F0=0时,U0=0,则此时

Uxy0-b1Y0=Uyy0-b2Y0=Uzy0-b3Y0=0

b1=B1,b2=B2,b3=B3

③对Z方向单向加载时,则有Fz0={0,0,Z0}T,输出信号则是Uz0={Uxz0,Uyz0,Uzz0}T。有

Uxz=c1Z+Uxz0-c1Z0
Uyz=c2Z+Uyz0-c2Z0
Uzx=c3Z+Uzz0-c3Z0

(13)

在Z0点附近进行多次标定,得

{0,0,Z1}T→{Uxz1,Uyz1,Uzz1}T
{0,0,Z2}T→{Uxz2,Uyz2,Uzz2}T
…

将所测Zi,i=1,…,N,Uxzi,i=1,…,N进行线性拟合,得直线

14(a)

同理可得:

14(b)

14(c)

如果三向力传感器采用压电晶桥或全桥应变测量,必有F0=0时,U0=0,则此时

Uxz0-c1Z0=Uyz0-c2Z0=Uzz0-c3Z0=0

c1=C1,c2=C2,c3=C3

经过以上3个方向分别标定后,其传感器可表示为

Ux=A1X+B1Y+C1Z
Uy=A2X+B2Y+C2Z
Uz=A3X+B3Y+C3Z

(15)

对方程组(15)求解,即得标定的结果

(16)

3 现场试验

本算法已经应用在实际项目中并取得比较好的效果。试验所用设备为100 t可保压KENT,下列表为现场试验中所测的部分数据。

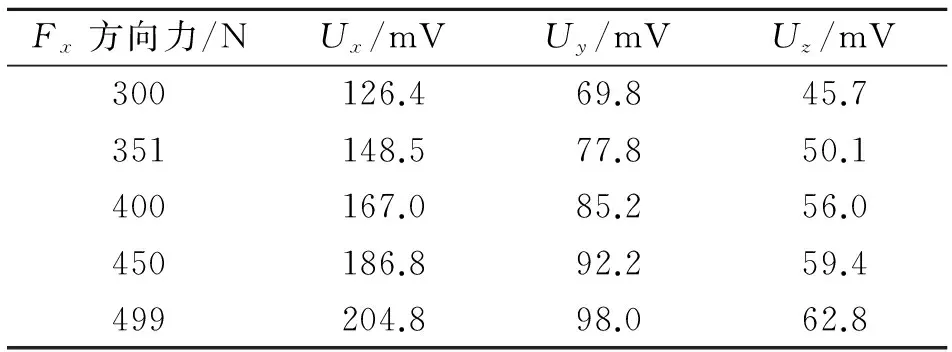
表1 X向单向加载标定时Ux、Uy、Uz

表2 Y向单向加载标定时Ux、Uy、Uz

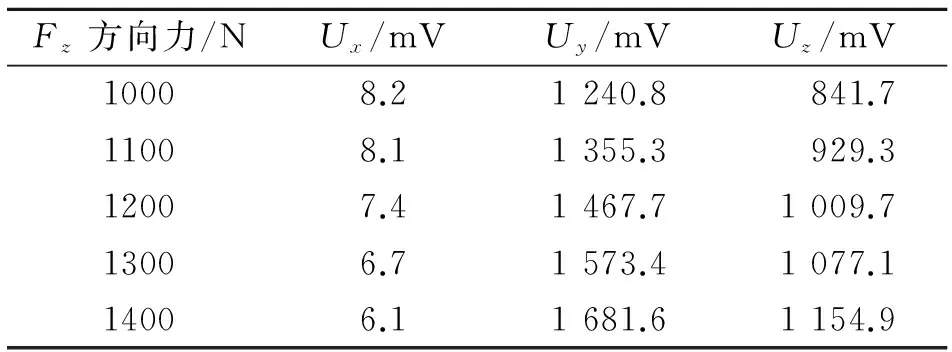
表3 Z向单向加载标定时Ux、Uy、Uz

采用最小二乘法对表中数据进行线性拟合分别得到:

A1=0.392628、A2=0.142490、A3=0.087535;
B1=0.0033、B2=0.423、B3=0.0954;
C1=0.58、C2=1.0997、C3=0.7742。

将以上数据代入式(15)可得:

Ux=0.392628X+0.0033Y+0.58Z
Uy=0.14249X+0.432Y+1.0997Z
Uz=0.087535X+0.0954Y+0.7742Z

用高斯消去法接上方程组,可以得出

X=3.017918Ux+0.715606Uy-3.277376Uz
Y=-0.190549Ux+3.433186Uy-4.733863Uz
Z=-0.387956Ux-0.568729Uy+2.245539Uz

为了验证该标定模型的可行性,对传感器进行单向加载,测量相对应的3个通道电压输出(Ux、Uy、Uz)如表4。

表4 三次单向加载时Ux、Uy、Uz

将电压值代入标定模型计算得3个方向分力为:X=192.27N、Y=1.36、Z=9.82。将其与真值(Fx=198、Fy=0、Fz=0)进行比较,不难看出该算法虽然存在一定系统误差,但在可接受的范围之内,说明该算法具有一定的可行性及准确性。

4 结论

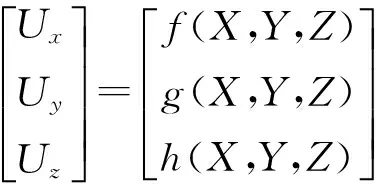
对于三向力传感器,一般标定时都采用单向加载。由于变形协调原因,每个单向加载在3个变形梁上都会有应变输出,如果直接代入标定方程,必然得到一个大样本的超定方程组,给其刚度系数阵定解带来困难。本算法则是通过对X向单向加载标定拟定得多组Ux、Uy、Uz,分别将输出与载荷对应数据进行线性拟合求出斜率A1、A2、A3;Y向单向加载可求出B1、B2、B3;Z向单向加载可求出C1、C2、C3。然后与原标定方程组进行比对,从而定解其系数阵。这样,标定样本再多,都可以通过线性拟合进行合并处理,从而获得更高的精度。本算法是在以作用力F为自变量,在某一点F0的一个邻域内作泰勒展开,所以传感器标定算法也应该分段量程标定,而且分段越细,算法系统误差越小。

本文仅采取线性标定的计算研究,算法涉及的误差分析研究留待以后进行。如果传感器线性度较差,则本算法不适用。这时,可按本文提供的思路,将传感器数学模型进行更高阶次的展开,得到更高阶方程组再代入标定数据计算。

[1] 林玉池. 测量控制与仪器仪表前沿技术及发展趋势[M]. 天津:天津大学出版社,2005:10-11.

[2]刘易华. 现代检测技术与测试系统设计[M]. 西安:西安交通大学出版社,1999:6-8.

[3]徐晓希,王伟国,吕春荣. 专用传感器加载定度装置和方法研究[J]. 机械设计与制造,2000,29(4):67-69.

[4]宋小奇,何伟铭. 灰色理论的位移传感器标定不确定度评定[J]. 传感技术学报,2012,25(11):1511-1515.

[5]何伟铭,蒋超伟,井原透,等. 高精度传感器标定曲线的预测拟合[J]. 传感技术学报,2013,26(11):1519-1524.

[6]Enrico Koppe,Daniel Augustin,Achim Liers,et al. Automatic 3D Calibration for a Multi-Sensor system[J]. 2012 International Conference on Indoor Positioning and Indoor Navigation,2012,12(6):978-983.

[7]王学水,邓铁六. 振弦式传感器标定曲线的拟合公式[J]. 传感器与微系统,1994(3):37-39.

[8]许林云,刘军,李赵春. 八角环式三向测力传感器的研究[J]. 南京林业大学学报(自然科学版),2008,32(4):121-124.

[9]李晓豁. 三向力传感器的设计及其标定[J]. 黑龙江矿业学院学报,1999,9(3):1-5.

[10]赵耀军. 煤炭三向截割力传感器特性研究[J]. 煤炭学报,2000,25(3):316-320.

[11]张晓辉. 机器人六维力传感器静态标定研究[J]. 自动化与仪表,2004(3),86-88.

[12]蒋凯,叶树明,陈杭,等. 适用于极端环境的高精度压力传感器开发与标定[J]. 传感技术学报,2007,20(10):2230-2233.

[13]唐文彦. 传感器[M]. 4版. 北京:机械工业出版社,2011:16-20.

[14]郭凤仪,郭长娜,王洋洋. MPSO-SVM的压力传感器的非线性校正研究[J]. 传感技术学报,2012,25(2):188-192.

[15]许靖中,谢锋,王从周,邢庭元. 三向压电晶体力传感器的研究[J]. 安徽工学院学报,1989,8(4):21-28.

[16]贾平明,张洪亭. 测试技术[M]. 第2版. 北京:高等教育出版社,2011:130-132.

席本强(1973-),男,博士,副教授,硕士研究生导师,主要研究方向为机电检测与控制;

何毅(1988-),男,硕士研究生,主要研究方向为机电液系统仿真与应用,908688386@qq.com。

TheCalculationMethodofThree-WayForceSensorCalibration

XIBenqiang*,HEYi

(School of Mechanical Engineering,LNTU,Fuxin Liaoning 123000,China)

This paper established the three-way force sensor’s general mathematical model from the abstract three input and three output mathematical model,then unfold the model as a first-order Taylor-series and ignored the error term like Lagrange remainder,finally get the three-way force sensor’s canonical equations which used to calculated linear calibration. Take the one-way repeated loading in three directions respectively,and used the least square method to fit the output data corresponding to the load,after comparing the fitting result with the original canonical equations can determine its coefficient matrix,finally derived the calibration algorithm. Just assumed the three strain beam of sensors is orthogonal during the deriving of this algorithm,and considering the three-deformation coupling relationship at the same time,have not limited the specific structure of sensor,so this algorithm can be used in different structure’s sensor. This algorithm provides a new train of thought and research methods for the calibration of multi-directional coupling type sensor.

Three-way force sensor;algorithm;calibration;model;coefficient matrix

2014-05-18修改日期:2014-07-17

10.3969/j.issn.1004-1699.2014.09.007

TP212.1

:A

:1004-1699(2014)09-1187-04