基于单张平面靶标的视觉测量系统快速校正研究

沈国峰，程筱胜，崔海华，戴 宁

(南京航空航天大学 机电学院，江苏 南京 210016)

基于单张平面靶标的视觉测量系统快速校正研究

沈国峰，程筱胜，崔海华，戴 宁

(南京航空航天大学 机电学院，江苏 南京 210016)

为解决双目测量系统传统标定方法过程复杂、应用条件苛刻、很难满足应用过程中准确快速校正的难题，提出了一种简便的校正算法。该算法仅需采集一张平面靶标图像，然后利用多视图几何中的绝对二次曲线特性，即可实现双目测量系统结构参数的校正优化。实验表明，利用该算法可以达到初始标定的精度，满足实际应用的可靠性需求。

双目测量；三维重建；系统校正；结构参数

双目测量系统是一种基于计算机视觉理论，并结合数字图像处理、软件开发等技术而组成的高精度测量平台。为使测量系统在应用过程中保持较高的精度，需要对其进行不定期的校正。通过观察发现，轻微的振动对测量系统精度的影响较大，而温度、湿度等环境参数在一定范围内的变化对其影响相对较小，可近似忽略。进一步的实验分析表明，系统的测量精度下降主要是由于其结构参数的变化引起的，因而校正过程主要是针对结构参数进行的。

对双目测量系统结构参数的校正实质上就是对左、右摄像机外参数的重新标定，从而重新确定图像像素坐标与世界坐标系之间的投影关系。摄像机的标定方法主要可以分为自标定和经典的摄像机标定方法两类。其中自标定方法[1-3]又可以细分为基于平移或旋转运动的自标定技术、利用本质矩阵和基本矩阵的自标定技术以及利用灭点并通过弱透视投影或平行透视投影进行的自标定技术等，由于自标定方法不需要标定物，仅仅依靠多幅图像对应点之间的关系直接对摄像机进行标定，因而这种方法相对灵活方便，但受标定精度及鲁棒性的限制，目前还只能应用于精度要求不高的场合。经典的摄像机标定方法主要有：Abdel-Aziz和Karara[4]提出的直接线性变换法(DLT)，通过求解线性方程组来估计摄像机的内外参数，运算简单，但是没有考虑实际应用中摄像机(尤其是广角摄像机)的畸变影响，从而造成标定误差较大；Roger Tsai提出的基于径向约束的两步法[5]，首先根据计算机视觉中的透视变换原理求解摄像机的一部分参数，然后把这部分参数作为非线性优化的初始值，并引入摄像机畸变参数，通过迭代算法求解剩余的参数，相对于直接线性变换法，该方法的标定精度有一定的提高；Weng[6]提出了一种改进的两步法，首先求解无畸变摄像机模型的闭环解来估计摄像机的非畸变参数，然后通过非线性优化的方法将第一步得到的参数迭代求精，并将摄像机的畸变考虑进来，最终准确估计出摄像机的所有内外参数；张正友提出的基于2D平面靶标的标定法[7]，只要求摄像机在两个以上不同的方位拍摄一张平面靶标图像而摄像机和2D平面靶标图像可以自由移动，不需要知道具体的运动参数。该方法的突出特点就是精度要比自标定方法高而标定步骤要较经典摄像机标定方法更为灵活方便。

本文以牙模测量系统为对象，利用实验的方法对系统结构参数快速校正的方法进行研究。在实验过程中假定左右摄像机的内参数已知且保持不变，通过采集单张平面靶标图像完成系统快速校正，并通过对靶标图像上的棋盘格角点进行三维重建来验证所提算法的可行性。

1 系统校正方法

1.1双目系统模型

双目测量是指采用双目视觉方法，通过左、右两个摄像机从不同角度采集同一物体图像来测量物体上某些特征点的空间三维坐标并恢复物体三维形貌的过程。假定空间任意一点P在左、右摄像机上的图像点p1，p2已经从图像中检测出来，则有摄像机模型：

(1)

(2)

式中：(u1,v1,1)与(u2,v2,1)分别为p1，p2点的像素齐次坐标；(x,y,z,1)为点P在世界坐标系下的齐次坐标；A1,A2为左、右摄像机的内参数矩阵;R1,T1,R2,T2分别为左、右摄像机的旋转矩阵与平移向量，也称系统结构参数；s1，s2为非零因子。

式(1)和式(2)分别包含3个方程，消去s1,s2后得到关于X,Y,Z的4个线性方程，利用最小二乘法即可求解唯一的(X,Y,Z)。

1.2校正方法

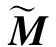
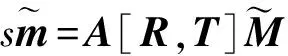
(3)

式中：参数s为任意非零尺度因子；旋转矩阵R与平移向量T称为摄像机外参数矩阵，也是本文需要校正的参数，A为摄像机内参数矩阵；(u0,v0)为主点的坐标；αu,αv分别为u轴与v轴的尺度因子。本文假定内参数在双目测量系统组装前已精确标定，在校正过程中仅作为已知参数。不失一般性，在此假设靶标平面位于世界坐标系的xy平面上，即z=0，并记旋转矩阵R的第i列为ri，则由式(3)可得[8]：

(4)

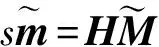
(5)

式中：H为3×3的矩阵，且H=λA[r1,r2,T]，其中λ为一常数因子。记H=[h1,h2,h3]，则有：

[h1,h2,h3]=λA[r1,r2,T]

(6)

式中：平移向量T为从世界坐标系的原点到光心的矢量；r1,r2为图像平面两个坐标轴在世界坐标系中的方向矢量，显然平移向量T不会位于r1,r2构成的平面上。由于r1,r2相互正交，因此det([r1,r2,T])≠0，又由于det[A]≠0，从而det[H]≠0。

1.3透视投影矩阵计算

假设在校正过程中图像受到高斯噪声干扰，高斯噪声满足正态分布，其协方差矩阵为Λmi，又由于各点的获取过程是独立的，令Λmi=σ2I，即协方差矩阵为对角阵，且各对角元素相等。使用最大似然估计法获取透视投影矩阵时，可以将所有对应点的Mahalanobis距离作为目标函数，如式(7)所示，当Mahalanobis距离最小时的H矩阵就是所需求解的透视投影矩阵。

(7)

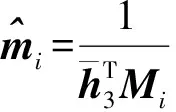
1.4系统结构参数的分离求解

当透视投影矩阵H求解后，加上已知的内参数矩阵A，则根据式(6)很容易求得系统的外参数：

(8)

式中：λ=1/‖A-1h1‖=1/‖A-1h2‖。

在上述校正过程中，还未考虑左、右摄像机的镜头畸变，因此需要在靶标图像角点检测前利用已知内参数对左、右图像作畸变校正操作，以补偿畸变产生的影响，同时也简化了三维模型的重建。

2 实验结果及误差分析

为验证算法可行性，本文进行了模拟实验，搭建如图1所示的双目测量系统，该系统由2台德国映美精工业相机(型号DMK 41BU02，分辨率1 280×960)，1台惠普PC机，1块平面棋盘格靶标板(7行×7列，15mm×15mm)，1个机械升降台组成。该测量系统初始内参数见表1，原始系统对靶标板角点进行三维重建的平均误差为0.133mm。

表1 左、右摄像机的内参数

图1 实验中搭建的双目测量系统

利用本文提出的方法对测量系统进行校正实验，校正后得到的系统结构参数见表2，同样对靶标板角点进行三维重建，记录重建误差；然后轻微地改变左、右摄像机的方位后重新进行上述校正实验，共进行3次，最终的三维重建误差结果见表3。

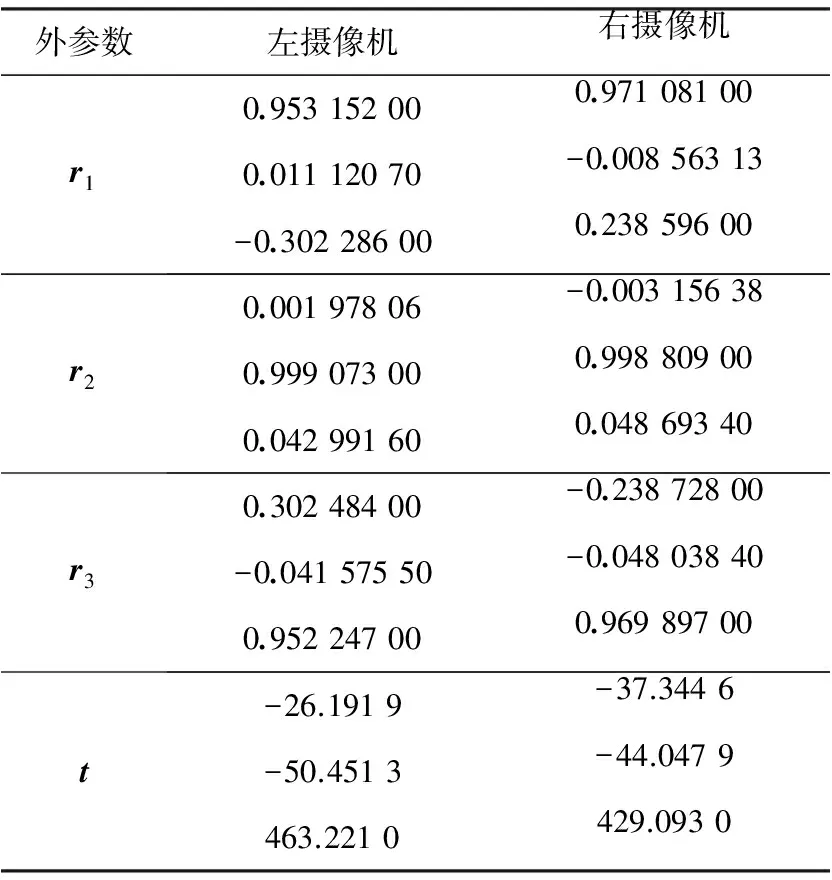
表2 左、右摄像机的外参数

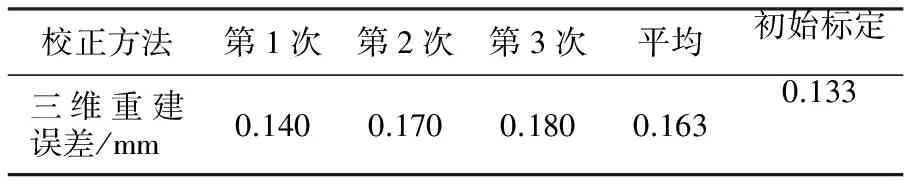
表3 三维重建误差比较(欧氏距离)

通过对表3中三维重建误差的对比分析可知，利用本文提出的校正方法对双目测量系统进行校正，既满足了校正过程的快速有效，同时又保证了实际应用中的测量可靠性需求。

3 结束语

双目测量系统的快速有效校正是保证测量可靠性的关键。本文提出的仅用单张平面靶标图像对系统结构参数进行校正的方法，方便用户在测量过程中快速有效地对系统进行校正。事实上，内参数在使用过程中的微小变化还是会对系统的测量精度产生一定的影响，因此还需要进一步研究出一种既保证快速有效，同时又能校正全部参数的校正方法，从而改善校正效果，进一步提高双目测量系统的可靠性。

[1] Hartley R．An algorithm for Self-Calibration from several views[C]// Computer Vision and Pattern Recognition，June, 1994, Seattle, Washington, USA． [S.l. ]：IEEE, c1994：908-912.

[2] Maybank SJ，Faugeras OD. A theory of self-calibration of a moving camera[J]. International Journal of Computer Vision，1992, 8(2): 123-151.

[3] Pollefeys M, Koch R, van Gool I. Selfcalibration and metric reconstruction in spite of varing and unknown internal camera parameters[J]. International Journal of Computer Vision，1999，32(1): 17-25.

[4] Abdel-Aziz Y I, Karara H M. Direct linear transformation into object space coordinates in close-range photogrammetry[C]// ASP Symposium on Close-Range Photogrammetry, Univ. of Illinois at Urbana Champaign．Urbana：American Society of Photo grammetry，1971: 1-18.

[5] Tsai R Y. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses [J]. IEEE Journal of Robotics and Automation, 1987, 3(4)：323-344.

[6] Weng Juyang, Paual cohen, Marc Herniou. Camera calibration with distortion models and accuracy evaluation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14(10)：965-980.

[7] Zhang Z. A flexible new technique for camera calibration [R]. Redmond, WA, USA：Microsoft Research，c2000: 1330-1334.

[8] 马颂德, 张正友. 计算机视觉——计算理论与算法基础[M]. 北京：科学出版社,1998.

ResearchonRapidCorrectionoftheVisionMeasuringSystemBasedonSinglePlaneTargetImage

SHEN Guofeng, CHENG Xiaosheng,CUI Haihua,DAI Ning

(Nanjing University of Aeronautics and Astronautics, Jiangsu Nanjing, 210016, China)

It is rather difficult to rapidly and conveniently correct owing to the complexity and application condition of the traditional calibration method. In order to solve this issue, this paper proposes a simple and rapid correction algorithm, which only needs a single plane target image with the characteristics of absolute conic in the multiple view geometry. The experimental results show that the initial calibration precision can be achieved and the practical application demand can be satisfied by the proposed algorithm in this paper.

Binocular Measuring; 3D Reconstruction; System Correction; Structure Parameters

10.3969/j.issn.2095-509X.2014.07.013

2014-06-07

国家科技支撑计划项目(2009BAI81B02)

沈国峰(1988—)，男，江苏苏州人，南京航空航天大学硕士研究生，主要研究方向为视觉检测、视觉测量等。

TP242

A

2095-509X(2014)07-0057-04