线性平移在捕食者—食饵数学模型稳定性分析中的应用*

华极鑫,冯维龙,王 娜,姜玉秋

(吉林师范大学 数学学院,吉林 四平 136000)

考察共同生活在一确定的理想环境内的捕食种群和食饵种群，假定没有迁出和迁入发生，由于生育、死亡和种群的相互作用，两种群的数量将随着时间变化.由于部分捕食者以一种食饵为食，食饵通常会被杀死[1](捕食者食动物)或者造成很大的损害[1](捕食者食植物).为了预测捕食种群和食饵种群数量的变化规律，20世纪20年代Volterra提出了比较完备的捕食者-食饵系统的数学模型[2]，一般形式为：

(S)

那么为了更好的讨论捕食者和食饵相互间关系，建立如下模型：

(M)

其中r1>0，r2>0，b>0，d>0,a>0,c=kb>0.

x(t)和y(t)分别表示t时刻食饵与捕食者的数量或密度；r1为食饵种群的内禀增长率，-r2表示不存在食饵时捕食者的死亡率；-ax2和-dy2分别为食饵和捕食者的种群密度对种群规模增长的抑制项(密度制约项)；c=kb表示当存在食饵种群时，捕食者对被捕食食饵的转化率(k为转化系数)；-bxy为t时刻有y个捕食者吃掉食饵的总数量.

本文将对模型(M)运用数学理论和方法对其平衡点的稳定性进行全面分析.

1 预备知识

为了方便讨论，对于捕食者-食饵系统模型(M)给出相关定理及符号.

定理1[3]对于非线性系统

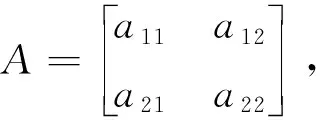
定理2 (1)q>0，p>0，Δ>0(两特征根为不同实根且同号)，则平衡点渐近稳定；q<0，则平衡点不稳定；(2)q>0，p>0，Δ=0(特征根为重根)，则奇点渐近稳定；p<0，则平衡点不稳定;(3)q>0，p>0，Δ<0(两共轭复特征根)，则奇点渐近稳定；p<0，则平衡点不稳定；p=0，平衡点稳定，但非渐近稳定.

定理2对于平衡点(0,0)的稳定性分析很容易，那么对于平衡点不是(0,0)时，我们就得利用平移变换不改变平衡点的稳定性态的性质，对此平衡点作平移变换[4].

2 系统分析

2.1 系统平衡点稳定性的分析

对于系统

考虑捕食者和食饵的实际生物学的涵义，我们在D={(x,y)|x≥0,y≥0}中讨论.

其相应的自治系统

(1)对p1(0,0)，根据定理1.1，可知其线性近似系统为

λ2+(r2-r1)λ-r1r2=0,

其中p=-(r1-r2)，q=-r1r2<0,p0(0,0)为鞍点，故p1不稳定.

代入系统(M)中，有

其特征方程为

代入系统(M)中，有

整理后得其线性近似系统为

其特征方程为

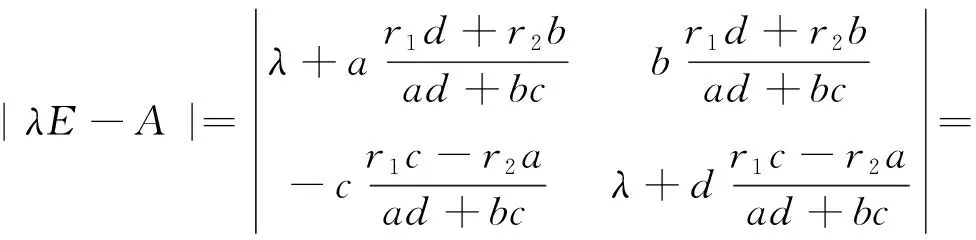
其中

利用根与系数的关系，得

时，p3渐近稳定.

2.2 MATLAB数值模拟结果

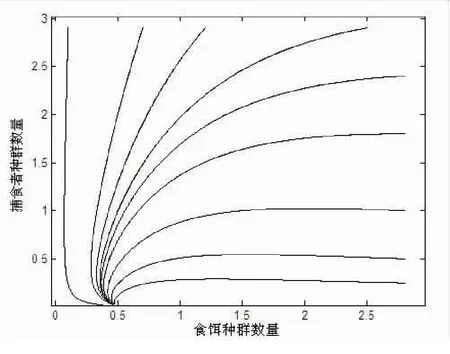
图1 p2渐近稳定

图2 p3渐近稳定

3 生物意义及应用

利用捕食这种生态学现象，可以限制种群的分布[5]和抑制种群的数量，如果受抑制的种群是有害动物的话，那么捕食现象就可以用于防治目的.比如我们日常生产中，尤其是农业上，害虫会损害农作物，使农作物减产，如果引入适当数量害虫的天敌，把天敌看作捕食种群，害虫是食饵种群，这就构成了捕食者-食饵相互作用系统，既控制了害虫所害农作物，又省去了用农药污染环境的麻烦.再如我国特有的珍稀水生兽类白鳍豚面临濒临灭绝的危机，利用捕食种群和食饵种群间的相互作用关系，我们可以人为的投放鱼类(食饵)，禁止捕杀白鳍豚(捕食者)，创造适合白鳍豚的生存的环境资源.

由此可见，对捕食者-食饵系统数学模型的研究，可以帮助我们利用捕食种群和食饵种群间的相互作用关系，来预测种群随时间的变化规律，或者人工干预对某些珍稀种群进行保护、开发和利用，这一理论的应用对人类的可持续生存发展有重要的指导意义和经济意义.