能源价格对经济波动的影响分析

韩维春，李杨鑫，封 岩

(1.对外经济贸易大学 国际学院，北京 100029；2.首都经济贸易大学 经济学院，北京 100070)

一、引言

经济波动问题一直是各个国家宏观经济研究的重点之一，探寻经济波动背后深层次的原因具有重要的意义。20世纪70年代石油危机引发的经济大萧条，使得人们将能源冲击纳入到宏观经济问题尤其是经济周期波动问题的研究中来，能源价格对于经济的冲击不容忽视。国家统计局2013年2月22日公布的《中华人民共和国2012年国民经济和社会发展统计公报》显示，2012年全年能源消费总量36.2亿吨标准煤，比上年增长3.9%，但原煤产量为36.5亿吨，比上年增长3.8%，增幅为近6年来最低；原油产量比上年增长2.3%。原油消费量增长6.0%；天然气产量比上年增长4.4%，而消费量增长10.2%。截止到2012年12月31日，对于石油这个备受世界关注的能源，中国对外依存度已达57%。由此可见，对于处于工业化中后期的中国，考察能源价格冲击对经济波动的影响成为必要。

笔者在现有研究的基础上，在更符合中国实际的不可分劳动的RBC模型中尝试引入能源价格冲击因素，考察其对中国经济波动的适用性以及解释能力，同时分析能源价格冲击与技术冲击对经济波动的影响。

二、中国经济波动的特征事实

本文利用计量经济学软件，考察产出(Y)、消费(C)、就业(H)、投资(I)、资本存量(K)*数据来源《2013年中国统计年鉴》相互之间的关系。

(一)数据处理

产出：将1978～2012年名义GDP折算成以1978年为基期(1978=100)的实际GDP。

消费：将居民消费支出按消费价格指数折算成1978年为基期的实际消费。

就业人数：由于1990年中国统计就业人数的方法有所改变使得就业人数显示出不正常的波动，本文利用张军和章元(2003)[11]的方法将1978～1989年的就业人数按1990年后的计算方法进行调整得到1978～2011年的就业人数。

投资：投资额用固定资本形成总额代替，并依据固定资产价格指数调整到1978为基期的实际值。

资本存量：本文的资本存量直接运用单豪杰(2007)[12]得到1978～2006年的资本存量，并运用其计算方法计算出2007～2012年的资本存量。

(二)结果分析

首先将上述所得数据先取对数，再通过Eviews软件中的H-P滤波去掉趋势项，得出主要经济指标相关系数。

表1 主要宏观经济变量相关关系表

从表1可以看出，资本、消费以及投资的波动成分与产出的波动成分之间是正相关，即是顺周期的，尤其是消费显示出强顺周期；而就业与产出是负相关，显示出弱负周期性。

三、模型构建与校准

(一)模型选择

在正式建立本文的模型之前，首先要理解标准的RBC模型(基本的RBC模型)与不可分劳动模型的区别。不可分劳动的Hansen模型*“不可分劳动的Hansen模型”是Hansen(1985)在论文《Indivisible Labor and the Business Cycle》中第一次在标准RBC模型中引入了劳动的非凸性，认为代表性主体要么以固定的时间工作要么就根本不工作，总工时数由就业人数确定。与基本的RBC模型区别在于引入了劳动的非凸性，即代表性主体要么以固定的时间工作要么就根本不工作，总工时数由就业人数确定。这一假设是符合中国的实际的，因为逐渐工业化的中国，越来越标准化的生产模式使得工人的工作时间通过合同的形式固定在不变的数量上。工人必须按照公司企业的规定要么工作全部的工作日(一般一天8小时)，要么不工作。因此，不可分劳动的Hansen模型是符合中国的实际的。

(二)模型的建立

不可分劳动模型除了效用函数与基本模型不一致以外，其他的约束条件不变，与基本RBC模型不同的地方在于引入了劳动的非凸性，同时将能源价格引入到模型中。本文先给出不可分劳动模型的效用函数。

在基本的RBC模型中引入不可分劳动的假设，即经济主体要么全部时间(H0)工作，要么不工作。家庭和厂商之间签订合同(保证消费集为凸)，即在时期t时个人以ωt的概率选择工作H0小时，以1-ωt的概率选择不工作，且是否工作都会获得相同的工资，即不工作的人也会拥有一份失业保险。因此总工时数Ht=ωtH0，那么不可分劳动模型的效用函数为：

U(Ct,ωt)=ωt[lnCt+Aln (1-H0)]+(1-ωt)(lnCt+Aln 1)

(1)

化简为：U(Ct,ωt)=lnCt+Aωtln (1-H0)。

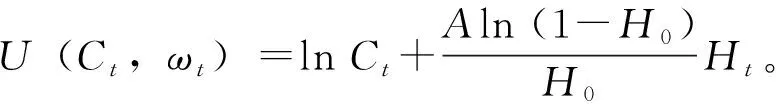
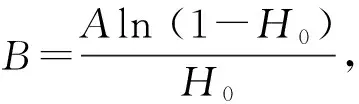
U(Ct,ωt)=lnCt+BHt

(2)

1.目标函数：

在不可分劳动的Hansen模型中引入能源价格冲击，效用函数不变，则期望效用的目标函数为：

(3)

其中，E为期望算子；β为主观贴现率，β∈(0，1)。

2.预算约束方程：

(4)

3.存量方程：

Kt+1=(1-δ)Kt+It

(5)

其中，Kt+1和Kt分别是t+1时期和t时期的资本存量，It表示t时期的投资量，δ表示折旧率，δ∈[0，1]。

4.生产函数：(规模报酬不变)

(6)

其中，α、θ和γ分别表示资本、劳动和能源的投入占比，At表示技术冲击。

5.冲击函数：

技术冲击函数：技术冲击服从马尔科夫过程(一阶自回归过程)：

(7)

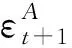
能源价格冲击函数：能源价格冲击同样也服从一阶自回归过程：

(8)

由于假设市场是完全的，则企业的收入正好等于家庭的预算，即

因为It=Kt+1-(1-δ)Kt，所以有：

则模型要解决的问题为：

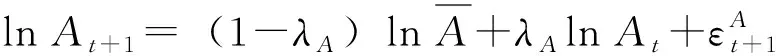
此问题的Bellman方程为：V(Kt,At,Pt)=max [lnCt+BHt+βEtV(Kt+1,At+1)]， 受约束于①、②、③，解得：

γYt=PtQt

至此，模型的建立已完成。

(三)静态均衡解

从而得到各变量稳态时的表达式：

(四)对数线性化方程*对数线性化方法一般有两种，一种是先将相关方程取对数，再对其进行一阶泰勒级数展开。第二种方法是Uhlig提出的一种更为简单的对数线性方法，不需要求导，但结果与前种方法一致，本文采用的是Uhlig提出的方法。具体过程感兴趣读者可以向笔者索要。

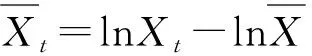
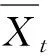
将模型中的方程一一进行线性对数化，得：

该模型共有八个变量，其中内生的状态变量为Kt，外生的状态变量为At和Pt，内生的控制变量为Yt、Ct、Ht、Qt、rt。将所得的八个方程写成以下形式：

(9)

(10)

(11)

(五)模型参数的校准

1.针对不可分劳动模型中的B值得确定

2.主管贴现因子β

黄赜琳(2006)[13]基于1978-2002年物价水平平均上涨6.6%这一事实设定其贴现因子β为0.935；贺云松(2010)[14]采用的也是黄赜琳的研究成果，取贴现因子为0.935；吕朝凤和黄梅波采用黄赜琳(2005)[16]的计算方法，设定贴现率β=0.97，因此本文采用吕朝凤和黄梅波的最新计算结果，取β=0.97。

3.资本折旧率δ

对于资本折旧率不同研究学者给出不同的取值。如王小鲁和樊纲(2000)[17]选取的值是0.05；陈昆亭和龚六堂(2004)[18]，孙宁华和江学迪(2012)[8]给出的都是0.1，因此本文笔者采用大多数学者的研究成果，取δ=0.1

4.生产函数中资本、劳动、能源所占份额α、θ、γ

本文采用孙宁华和江学迪(2012)[8]的研究结果，资本的所占份额α为49.3%，劳动的所占份额θ为34.9%，能源的所占份额γ为15.8%。

5.技术冲击参数λA和σA

孙宁华和江学迪(2012)[8]得到技术冲击一阶自回归系数λA=0.718，随机扰动项标准差σA=1.9%。黄赜琳(2006)[13]技术进步：0.727，2.46%，本文采用黄赜琳的研究结果，将技术冲击一阶自回归系数λA设定为0.73，随机扰动项σA设为2.46%。

6.能源价格冲击参数λP和σP

魏巍贤、高中元和彭翔宇(2012)[9]得出λP=0.2640，σP=0.1355，但是作者在其模型中引入了五个外省的冲击变量，与本文研究对象有出入。本文能源价格冲击参数的设定采用孙宁华和江学迪的结果，一阶自回归系数λP=0.957，σP=1.562%。

根据以上参数的校准值可以计算出稳态时变量值：

对方程组(9)、(10)、(11)利用Dynare软件进行编程并利用Matlab软件输出结果，得到均衡状态下的宏观经济变量的标准差和相关系数，并与实际数据进行对比分析，结果如表2所示：

表2 模型模拟经济的周期波动特征表

表中的K-P比率是用模拟经济变量的标准差除以实际经济对应变量的标准差，其含义说明了模型的解释程度，比值越大，解释程度越好，即模型的模拟程度越好。

由上述模拟结果可知，模型模拟的产出标准差为0.029，而实际的标准差为0.031，模型解释了实际产出波动的93.55%，拟合结果比较好。

从消费来看：模型模拟的消费标准差为0.0338，而实际消费的标准差为0.038，K-P比率为88.95%，即模型能解释实际消费波动的88.95%。除此之外，模型与实际经济的消费与同期的产出相关系数都为正，而且都大于0.5，都表现出较强的顺周期。

从资本来看：模型模拟的资本标准差仅为0.0063，是实际数据标准差的16.8%，即模型只能解释实际资本波动的16.8%，笔者认为这可能是实际资本存量的计算方法的选择带来的数据偏差所致，这一点还需进一步细化和探讨。

从就业来看：从就业波动来看，模型模拟的就业波动远大于实际就业的波动，是实际波动的223.0%，这主要是因为笔者对中国实际就业人数进行了处理，将1990年之前的就业人数按照1990年之后的统计方法进行调整，减小了实际就业的波动程度，这样K-P比率变大也就不足为奇了。除此之外，从就业与同期产出相关系数看出，模型经济的就业人数与产出是呈正相关的，而实际就业产出呈现的是弱负周期，这同样是由于上述原因所致。

从投资角度来看，模型解释了实际投资波动的63.93%，解释程度较好，而且模型和实际投资与同期产出的相关系数都为正，可见投资是顺周期的。

根据模型的模拟数据，可以建立技术冲击和能源价格冲击的脉冲响应函数，利用脉冲响应图来表达。以横坐标代表0到40期的时间间隔，纵坐标分别代表产出、消费、资本、就业、资本收益率以及能源产量对于技术冲击与能源价格冲击的反应程度，根据模拟数据，建立如下技术冲击与能源价格冲击的脉冲响应图：

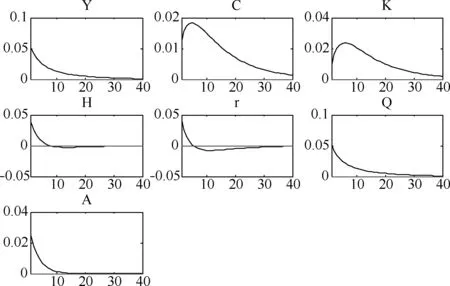
图1 技术冲击的脉冲响应

图2 能源价格的脉冲响应

从两个图来看，技术冲击的效应大于能源价格冲击，因为技术的变革或改善会直接促进生产效率的提高，从而使得产出迅速增加；而能源价格冲击一般是通过间接的途径来影响到经济各变量，该产出带来负效应。

由技术冲击的脉冲响应函数可以发现，技术的正向冲击对于产出、消费、资本即投资都有永久性性的正向作用；对于劳动短期内有较强的正向作用，经过一段时期后这种正向冲击会减弱甚至小于0；对于资本收益率开始会是正向的到后期为负，主要是边际收益率递减规律带来的结果。

由能源价格冲击的脉冲响应图，能源价格对于产出、消费、资本等经济变量都是带来负效应的；对于就业来说前期是负效应，到了后期会产生微弱的正向冲击，这主要是因为前期能源价格的上涨会导致生产成本上升，产量下降，则失业率增加，之后随着这种产出负效应的减弱使得生产成本逐渐降低，就业率会有所上升。

综上所说，技术冲击和能源价格冲击对于经济都有一定程度的影响，虽然能源价格冲击不及技术的冲击冲击程度，但是其冲击的持久性比技术冲击要长，因此在减缓经济波动从而促进经济平稳发展的道路上，能源价格的波动仍是不可小觑的。

四、结论

本文模型模拟的结果表明，引入能源价格冲击的不可分劳动的RBC模型能够较好地解释中国经济的波动，其中解释了实际产出波动的93.55%，消费的K-P比率为88.95%，这两者的解释力很高。但是对于资本的解释力只有16.8%，笔者认为不应是模型的建立问题，而是在处理资本数据的方法上有待改进。除此之外，由于本文所建立的模型只考虑了两部门，并未将货币、财政支出、对外贸易等因素考虑进来，这将直接导致模型中有些变量的解释力有所偏差，这一点是以后进一步需要研究和考察的。

本文利用脉冲响应函数分析了技术冲击和能源价格冲击对主要经济变量的影响。结果表明技术冲击的程度要大于能源价格冲击，但是能源价格冲击的影响更持久，所以在通过政策减缓经济波动的过程中能源价格方面应该得到重视。首先政府应加强能源价格的调控，高度重视能源安全问题；第二是要做好能源战略储备工作，减少能源供给的紧张而带来的不安定因素；第三是要加快新能源开发的步伐，从而降低污染降低生产成本，保证经济的可持续发展；最后就是加强各个国家，各个地区的能源合作以实现资源的最优化利用。

参考文献：

[1]Hansen G D.Indivisible Labor and the Business Cycle[J].Journal of Monetary Economics,1985，(16)：309-27.

[2]张军，章元.对中国资本存量K的再估计[J].经济研究，2003，(7):35-90.

[3]单豪杰.中国资本存量的再估算:1952～2006年[J].数量经济技术经济研究，2008，(10):17-31.

[4]黄赜琳.技术进步与就业波动变化的影响分析基于可分劳动RBC模型的实证检验[J].统计研究,2006，(2):34-38.

[5]贺云松.基于引入习惯形成的RBC模型的中国经济波动分析[J].经济纵横2010，(16)：105-106.

[6]吕朝凤，黄梅波.偏向性技术变迁、习惯形成与中国经济周期特征——基于RBC模型的实证分析[J].经济评论,2012，(2)：31-43.

[7]黄赜琳.中国经济周期特征与财政政策效应——一个基于三部门RBC模型的实证分析[J].经济研究,2005，(6):27-39.

[8]王小鲁，樊纲.中国经济增长的可持续性[M].北京：经济科学出版社出版，2000.

[9]陈昆亭，龚六堂.中国经济增长的周期与波动的研究——引入人力资本后的RBC模型[J].经济学(季刊),2004，(3)：803-808.