深孔钻杆系统扭振动力减振器优化及仿真研究

中北大学机械与动力工程学院 陈艳玲

引言

在机械制造行业，尤其是重型机械行业中，深孔加工的地位是非常重要的[1]。在深孔钻削加工中，由于钻杆又细又长，振动对加工精度、切削效率以及刀具耐用度都影响很大。钻杆扭转振动产生的原因主要有：1.工件材质的不均匀；2.钻杆的抗扭刚度较弱。现针对钻杆扭振采取的措施主要有[2]：1.控制切削用量；2.尽可能提高动力传递系统的刚度；3.合理设计和改进钻头的结构；4.使用动力减振器。

本文研究的是通过附加扭振动力减振器来对钻杆系统减振。首先对深孔钻削扭振减振系统进行简化，建立钻杆系统的动力学方程，再用一加工实例来说明系统中各项参数的确定，以及动力减振器的结构参数的设计并对各项参数进行优化，最后利用Simulink软件对附加动力减振器前后的钻杆系统进行动力学仿真对比，验证经过优化的动力减振器取得了良好的减振效果。

1 钻杆系统动力学方程的建立

在深孔钻削过程中，钻杆容易产生扭振，在钻杆支架上安装动力减振器，可以有效抑制钻杆的扭振。动力减振器安装在BTA深孔钻床上的位置如图1[3]。

图1 动力减振器在钻床上安装位置示意图

根据深孔钻削加工的特点，可将深孔钻削系统视为单自由度系统，因此附加动力减振器后的减振系统，可简化为图2所示情形[4-5]。

图2 深孔钻杆扭振模型

图3 减振系统力学模型

为了方便研究，这里选择附加一个动力减振器的模型进行分析[6]，如图3所示。

对于钻杆扭振系统，固有频率有无限多个阶次，工程上一般采用模态截断的方法。由于高阶模态对其加工精度等的影响较小，故可以忽略，仅考虑一阶模态扭振的减振问题。

设钻杆一阶模态转动惯量、阻尼和扭转刚度分别为I0、C0和K0，动力减振器的转动惯量、阻尼和扭转刚度分别为I1、C1和K1，且动力减振器结构示意图如图4所示。

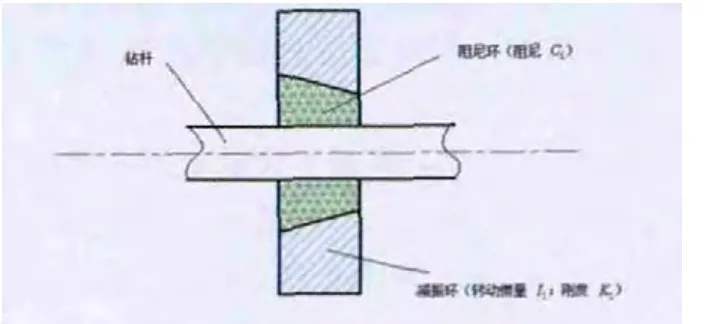
图4 动力减振器结构示意图

则系统受到频率ω的激励，运动方程为：

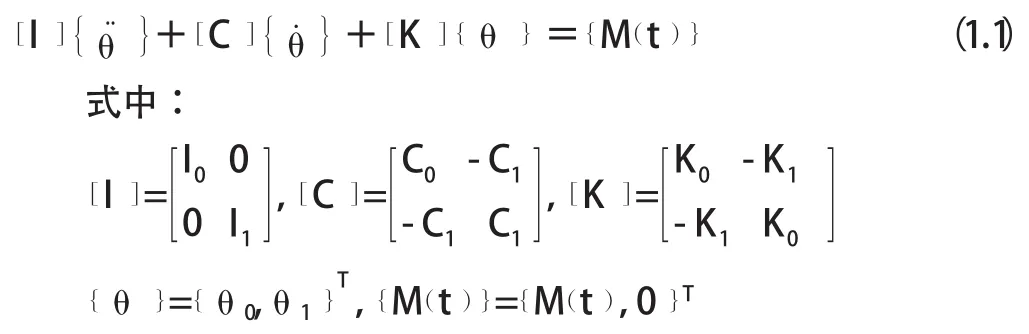
假设系统受ω频率的激励，没有动力减振器前，钻杆头部产生的角位移为θ0；使用动力减振器之后，钻杆头部产生的角位移为θ0，0。若系统受到的激励恒定，则钻杆头部产生的角位移为θ。

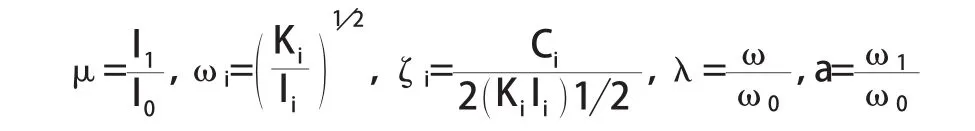
为了便于分析，引入下列状态变量：转动惯量比μ，钻杆的固有频率ω0，减振器固有频率ω1，钻杆系统的阻尼比ζ0，减振器阻尼比ζ1，频率比和调谐频率比a，其定义分别为：（1.1）式进行数学换算，可得到系统传递函数的表达式，从而可以得到系统动力放大系数的解析式。因为钻杆系统本身的阻尼很小，为简化计算，忽略钻杆系统的阻尼，即令ζ=0，由此，系统动力放大系数ε为：

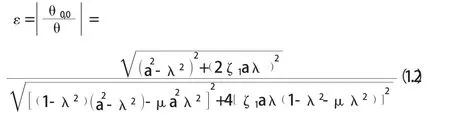
2 钻杆系统参数确定

用一加工实例来说明系统中各项参数的确定。

加工实例如下：

采用BTA系统加工孔径为D=50mm的工件，切削参数为：转速N=1500r/min，进给量f=0.1mm/r。选用的钻杆材质为40Cr，外径D0=46mm，内径Di=30mm，长度L=5000mm，钻杆材料的剪切模量G=82.8GN/m2，密度ρ=7.82×103kg/m3，钻杆截面极惯性矩J=π（D04-Di4）/32（m4），测得切削液40°C的粘度μ=30×10-6m2/s。则钻杆的扭转刚度：

3 动力减振器参数设计及优化

3.1 动力减振器的参数设计

动力减振器结构参数的确定，即确定I1、K1、C1，由于钻杆系统的I0，K0，C0是已知的，因此动力减振器的参数可通过确定参数 μ、a、ζ1得到[7]。

在深孔钻削加工中，激振频率变化的范围通常为，参考常规设计方法，的范围一般为，现取定；的范围一般为，一般设定动力减振器频率与钻杆系统固有频率相等的情况，即令；取值的范围一般为，现取定。

3.2 动力减振器的参数优化

3.2.1 动力减振器的参数优化目标

根据实际现场以及为解决实际生产中的具体问题，减振器的参数优化的目标函数主要有以下四个[8]：

（1）系统扭振动力放大系数极大值极小化；

（2）钻杆扭振角加速度极大值极小化；

（3）减振区域最宽；

（4）钻杆角位移均方值极小化。

3.2.2 动力减振器的参数优化方法

以系统扭振动力放大系数极大值极小化为目标函数，即以（min[maxε（λ）]）为例说明优化计算的过程。

三个参变量a、ζ、λ都有对应的取值范围，因此，可通过编写三组循环代码来实现求取所有最大值中的最小值，编写vba代码，程序框图如图5。

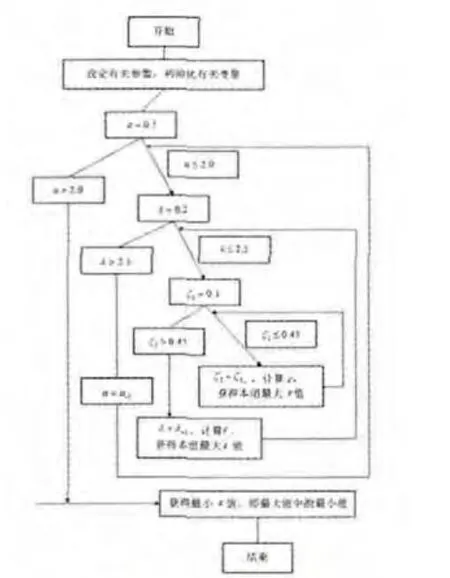
图5 程序框图

运行程序，得到参数优化后的结果：μ=0.4，a=0.71，ζ1=0.35，通过换算可得到实例中设计的动力减振器的各项结构参数：

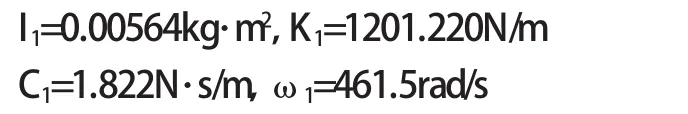
4 钻杆系统附加动力减振器仿真结果研究

4.1 传递函数

（1）未附加动力减振器之前：

钻杆减振系统的动力学方程：

代入数值，并通过MATLAB编写程序，可得到传递函数结果如图6：

图6 MAT LAB运行得到未附加动力减振器钻杆系统的传递函数

（2）附加动力减振器后：

钻杆系统的运动方程：

通过编写MATLAB程序可得到传递函数的结果如图7：

图7 MAT LAB运行得到附加动力减振器钻杆系统的传递函数

4.2 系统的输入

利用经验公式计算，得出扭矩的经验值，作为simulink的输入。

钻削过程中，计算切削扭矩的经验公式为：

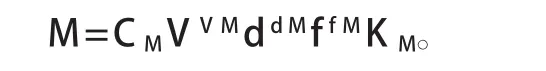
式中：CM为扭矩系数，v为切削速度（m/min），d为钻孔直径（mm），f为进给量（mm/r），vM、dM、fM等指数系数都是前人通过生产实践和实验得到，对于45钢材料CM=563.08，vM=0.05，dM=1.812，fM=0.918。

在此实例中，采用BTA系统加工孔径为D=50mm的工件，切削参数为：转速N=1500r/min，进给量f=0.1mm/r。

由此可得切削扭矩M=107.08N·m。

4.3 深孔钻杆系统扭转振动仿真

为了接近实际，首先从Source模块中选择（Sine wave）和（Band-Limited White Noise），输出二者相乘的信号作为切削扭矩信号，并且修改（Sine wave）的属性，设置其Amplitude为切削扭矩经验公式得到的值107.08，设置其Frequency为50π（由转速N=1500r/min换算得到）；添加两个（Transfer Fcn）模块，并分别修改其属性，设置（Transfer Fcn）模块num为[2.147e018]，den为 [1.708e014 1.393e016 1.081e020 3.514e021 1.227e025]，设置（Transfer Fcn1）模块 num为[70.92]，den为[10422500]；添加（Scope）模块用来输出波形，（Scope）用来将附加动力减振器前后的钻杆系统扭振振幅对比分析，仿真框图如图8。设置仿真时间为5s，运行，得到仿真结果：如图9所示。

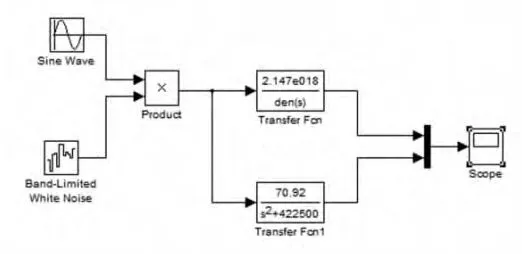
图8 仿真框图

图9 BTA钻杆系统附加动力减振器前后振幅对比图

由图9可直观的得出：钻杆系统附加经过优化后的动力减振器，钻杆扭振的扭转角明显减小。

5 结论

（1）在钻杆支架上安装动力减振器，可以有效抑制深孔钻削过程中钻杆产生的扭振。

（2）根据实际现场，以及为解决实际生产中的具体问题，选择目标函数，来优化动力减振器的各项结构参数。

（3）由仿真结果可得，经过优化的动力减振器对于深孔钻削中钻杆扭振扭转角的减小效果明显。

[1]王峻.现代深孔加工技术[M].哈尔滨：哈尔滨工业大学出版社，2005.

[2]李伯民.对深孔钻杆扭振的研究[J].太原机械学院学报，1986,15(3)：109-119.

[3]庞俊忠，陈艳玲.深孔钻削系统扭振动力减振器的优化设计[J].机械设计与研究，2013(6)：65-68.

[4]顾乾坤，唐一科，梁锡昌.深孔钻床扭转振动减振理论及实验研究[J].重型机械，1995(4)：58-61.

[5]顾乾坤，唐一科.动力减振器优化分析与设计[J].机械设计，1994(4)：27-29.

[6]L.D.Viet，N.D.Anh,H.Matsuhisa.The effective damping approach to design a dynamic vibration absorber using Coriolis force，Journal of Sound and Vibration[J]，2011（330）：1904-1916.

[7]顾乾坤，唐一科.深孔钻床工艺扭振系统动力减振器优化设计[J].机械设计与制造，1993(1)：30-32.