线性模型中总平方和分解公式的证明*

王剑红,杨素芳

(山西药科职业学院 基础部,山西 太原 030031)

线性模型中总平方和分解公式的证明*

王剑红,杨素芳

(山西药科职业学院 基础部,山西 太原 030031)

文中结合矩阵的知识,通过正交变换,给出了正交饱和设计对应的线性统计模型中总平方和分解公式的另一种证明方法，优化了文献[1]中对其的证明.

矩阵;幂等阵;正交矩阵;投影矩阵

对于正交饱和设计问题，通常可用如下的线性统计模型来描述

Y=β01n+β1x1+…+βmxm+ε=μ+ε

(1)

其中Y=(y1,y2,…,yn)T是观察值向量；xj=(x1j,x2j,…,xnj)/，j=1,2,…,m由试验设计来确定；矩阵X=(x1,x2,…,xm)为上述正交表H所对应的设计阵；β=(β0,`β1,…,βm)T；ε=(ε1,ε2,…,εn)/是误差向量，且εi(i=1,2,…,n)是相互独立同分布的随机变量，且有ε～N(0,σ2In).

由于模型(1)是基于正交饱和设计，故此时的误差平方和等于零，从而使总平方和SSj与各列的效应平方和之间有如下总平方和分解公式

SST=SS1+SS2+…+SSm,fT=f1+f2+…+fm成立.

这篇文章我们给出了总平方和SST与各列的效应平方和SSj之间的矩阵证明方法,优化了文献[1]中对其的证明.

1 预备知识

在一个试验设计中，当被考虑因子(包括交互作用)个数多到使得需估计参数的个数达到可估计参数的最大个数时，这样的试验设计称为饱和设计.当一个饱和设计又为一个正交设计时，称为正交饱和设计.

2 主要研究结果及证明

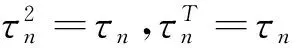
又注意到

Tj为对应设计阵第j列的置换矩阵，即Tj中只有0和1两个元素，而且每一行、每一列有且只有一个1，其余的元素全是0.由张应山的博士论文知,Tj具有存在性.

取

故

这样,对于模型(1)，各列的效应平方和

YTAjY,j=1,2,…,m.

且Pn,A1,…,Am为相互正交的投影阵.

因为

diag(Pr1,Pr2,…,Prm)Tdiag(Pr1,Pr2,…,Prm)=

diag(Pr1,Pr2,…,Prm)且Pndiag(Pr1,Pr2,…,Prm)=

Pn,PnAj=0,AiAj=0(i≠j).

所以Pn,A1,…,Am为相互正交的投影阵.

容易验证

τn=In-Pn=

所以SST=YTτnY=YT(A1+A2+…+Am)Y=

SS1+SS2+…+SSm.

总平方和自由度为fT=n-1,fj=pj-1为第j列平方和的自由度(j=1,2,…,m),而完全正交设计是指上述正交设计满足如下的等式n-1=(p1-1)+(p2-1)+…+(pm-1).

故SST=SS1+SS2+…+SSm,fT=f1+f2+…+fm.对比文献[1]和本文中证明的方法，显然用矩阵知识证明更为简洁.

[1]张晓琴.正交饱和设计的统计分析[J].应用概率统计,2007,23(1):91-102.

[2]张应山.正交表的数据分析及其构造[D].上海:华东师范大学博士论文,2006.

[3]茆诗松,周纪芗,陈颖.试验设计[M].北京:中国统计出版社,2004.

[4]张金槐.线性模型参数估计及其改进[M].长沙:国防科技大学出版社,1992.

[5]张应山.多边矩阵理论[M].北京:中国统计出版社,1993.

[6]程云鹏.矩阵论[M].西安:西北工业大学出版社,2002.

[7]余锦华,杨维权.多元统计分析与应用[M].中山大学出版社,2005..

(责任编辑:王宏志)

2014-01-05

王剑红(1971-),山西汾阳人,硕士,讲师.

O

A

1008-7974(2014)01-00032-03