浅谈一种建立自动扶梯刹车距离数学模型的新方法

胡 傲

(广州奥的斯电梯有限公司，广东 广州 510425)

浅谈一种建立自动扶梯刹车距离数学模型的新方法

胡 傲

(广州奥的斯电梯有限公司，广东 广州 510425)

介绍了一种建立自动扶梯刹车距离数学模型的新方法，并且使用这种方法对自动扶梯的部分结构参数进行了计算。与以前的建模方法相比，该方法最大的特点是直接根据自动扶梯的实际刹车距离来建立数学模型，而无需理会自动扶梯的内部结构。

自动扶梯；刹车距离；数学模型

0 引言

刹车距离是自动扶梯安全性的一个重要参数。为了能够准确预计自动扶梯的刹车距离，各大电梯公司及科研院所已经建立了多种数学模型[1]。但这些模型都是根据自动扶梯的内部结构推导出来的，它们的建立需要对自动扶梯的内部结构有充分的了解。此外，这些数学模型还包含了很多假设参数，如摩擦系数、传递效率等。因此在使用前，往往需要根据实际的测量结果进行校正。

本文尝试使用了一种新方法，即不理会自动扶梯的内部结构，只根据自动扶梯的实际刹车距离来建立其数学模型，并根据这个模型，对自动扶梯的一些结构参数进行了计算。该方法适合在不了解自动扶梯内部结构的情况下对自动扶梯的刹车数学模型以及结构参数进行估算。

1 自动扶梯刹车数学模型的推导

从能量转化的角度来看，自动扶梯的刹车过程可以看成自动扶梯以及载荷的动能Ek和势能Ep通过克服刹车力F和摩擦力f做功转化为热的过程，即：

Ek .Esc+Ek .Weight+Ep+W=0

式中，Ek .Esc和Ek .Weight为刹车前自动扶梯以及载荷的动能；Ep为刹车过程中载荷下滑减少的势能；W为刹车过程中刹车力F和摩擦力f所做的负功。

自动扶梯的刹车过程可以分为两个阶段：第一阶段，刹车系统已被触发，但其机械机构还没运动到作用位置。这一阶段，自动扶梯的刹车只受重力G和梯路摩擦力f的影响，近似处于自由下滑状态，其下滑距离为Sfree。第二阶段，刹车系统的机械机构已运动到作用位置。此时自动扶梯的刹车受到刹车力F、重力G和梯路摩擦力f的作用，开始减速下滑直至停止，其下滑距离为Sbrk。二者之和即总刹车距离S=Sfree+Sbrk。则上式可以转化为：

式中，m表示载荷的质量；v表示自动扶梯的运行速度；α表示自动扶梯的倾斜角。

相同的运行速度下，可以近似假设自动扶梯的Ek .Esc、Sfree和f为常数。并且在相同状态下，也可近似假设其刹车力F为常数。因此上式可以变形为：

(1)

表1展示了一个根据某自动扶梯在不同载荷下的刹车距离数据所建立的刹车数学模型。该自动扶梯倾斜角为30°，运行速度为0.5 m/s。

表1 根据刹车距离建立自动扶梯刹车数学模型

2 自动扶梯刹车数学模型的应用

2.1 自动扶梯刹车距离的预测

2.1.1 自动扶梯刹车距离的计算

在建立了刹车数学模型以后，就可以用它来预测不同载荷下自动扶梯的刹车距离。将式(1)变形，得到：

(2)

将自动扶梯的倾斜角度α、运行速度v、线性回归得到的参数a和b以及载荷质量m代入，就可以算出自动扶梯的刹车距离S。

2.1.2 自动扶梯刹车距离置信区间的估计

由于测量误差的存在，使a和b的回归分析结果存在一定的不确定性，这导致了刹车距离S的计算值与实际测量结果之间存在偏差。为了提高对S预测结果的可信度，就有必要对其置信区间进行估计。

为了表征a和b的不确定性，回归分析给出了它们的标准误差se，如表1所示。刹车距离S的标准差不能直接求得，是可以根据式(2)，使用Monte Carlo模拟对其进行估计，进而求出其置信区间[2-3]。

使用表1中“热态”的数学模型，我们对载荷为4 000 kg时，刹车距离S的95%置信区间进行了估算。首先根据参数a和b的值及它们的标准误差se，构建其正态分布模型；然后根据式(2)对刹车距离S的值进行了10 000次的Monte Carlo模拟，得到刹车距离对数lnS的分布，如图1所示。

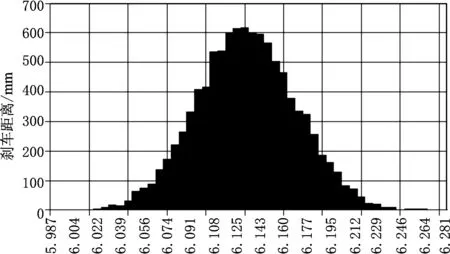
图1 使用Monte Carlo模拟得到刹车距离对数lnS的分布

依图1得到lnS分布的均值为6.130，标准差为0.037 07。据此计算出当载荷为4 000 kg时，该自动扶梯的刹车距离预计值是459.4 mm，有95%的可能是落在427.2～494.0 mm的区间内。

2.2 对自动扶梯刹车相关参数的计算

对于使用刹车片的刹车系统，在连续进行若干次刹车之后，刹车片会因摩擦发热而温度升高，从而导致摩擦力变大，我们把这种状态称为“热态”，与之对应的“冷态”就是指刹车片温度没有升高的状态。对于这一类型的自动扶梯，当其处于“热态”和“冷态”时，刹车力F的大小是不同的，而自动扶梯的Ek .Esc、Sfree和f的值则不受此影响。这样我们可以推导出以下关系：

热态：

冷态：

令：awarm=-Fwarm×Sfree-Ek .Esc，acool=-Fcool×Sfree-Ek .Esc，bwarm=Fwarm+f，bcool=Fcool+f，则根据自动扶梯处于热态和冷态下不同载荷的刹车距离数据，就可以算出awarm、acool、bwarm和bcool的值，建立起自动扶梯刹车系统在热态和冷态下的刹车数学模型。

在正常情况下，刹车力F是远远大于梯路摩擦力f的，即F+f≈F，则可以对自动扶梯刹车相关的结构参数进行计算。表2展示了根据表1中的刹车数学模型，对自动扶梯的刹车相关参数进行计算的结果。

表2 根据自动扶梯刹车数学模型对刹车相关参数的计算

2.3 对自动扶梯刹车片磨损速率的估算

自动扶梯的刹车片在使用过程中会因磨损而需要定期更换，更换时间与磨损速率有关。因此，我们需要估算自动扶梯刹车片的磨损速率，以确定刹车片的更换时间。

自动扶梯刹车片的磨损速率是根据刹车过程中其所吸收的能量来计算的，因此只要知道刹车片在刹车过程中吸收能量的大小，就能对其磨损速率进行估算。

根据Ek .Esc+Ek .Weight+Ep+W=0，可知自动扶梯刹车过程中刹车片吸收的能量有自动扶梯的动能Ek .Esc、自动扶梯载荷的动能Ek .Weight以及刹车过程中载荷下滑减少的势能Ep三部分。根据自动扶梯刹车的数学模型，可以估算出Ek .Esc；根据自动扶梯的运行速度以及人流量，可以估算出Ek .Weight以及Ep。这样就可以估算出自动扶梯刹车片的磨损速率了。

3 结语

根据自动扶梯在不同载荷下的刹车距离，可以建立起自动扶梯刹车距离的数学模型。而结合自动扶梯在热态和冷态下的刹车距离，可以求算出自动扶梯一些与刹车有关的参数。这种方法的好处是无需理会自动扶梯的内部结构。但是这种方法假设在刹车过程中刹车力F保持不变，因此不适用于刹车系统带自锁紧功能的自动扶梯。

[1]王薇，路俊秀.自动扶梯和自动人行道制动能力的计算[J].机械设计，2006(5)：18～19

[2]王岩.MonteCarlo方法应用研究[J].云南大学学报：自然科学版，2006(28)：23～26

[3]曲双石，王会娟.MonteCarlo方法及其应用[J].统计教育，2009(1)：45～55

2014-07-14

胡傲(1979—)，男，湖南长沙人，测试工程师，研究方向：自动扶梯认证测试。