双色散模型的辛时域有限差分算法∗
2014-08-31王辉1黄志祥1吴先良1任信钢3吴博1
王辉1)3) 黄志祥1)† 吴先良1)2) 任信钢3) 吴博1)
1)(安徽大学计算智能与信号处理教育部重点实验室,合肥 230039)
2)(合肥师范学院电子信息工程学院,合肥 230061)
3)(香港大学电机电子工程学院,香港,薄扶林道)
1 引 言
色散媒质在电磁场领域有着广泛的应用[1−3],比如等离子体,双负媒质,吸波材料等都属于色散媒质.如果媒质的介电常数或者磁导率是频率的函数,那么这种媒质被称为色散媒质.现实中的很多物质都是色散的,比如海水,雪等.由于色散媒质的复杂特性,使得解析法在求解色散媒质的电磁场问题上变的十分困难.因此对它们的研究只能借助于数值方法以及科学实验.在诸多数值方法中,时域有限差分方法(FDTD)[4,5]是研究色散媒质电磁特性的有力工具.因为FDTD方法具有宽带特性,一次运行可以得到宽频结果.电通量密度D和电场E,磁通量密度B和电场H之间的关系反应了材料的复杂性,很多时候并不简单的假设本构关系式D=εE,B=µH中的ε,µ是一个恒定的标量,ε,µ可以是一个张量,从而可以描述媒质的各项异性.当研究非线性媒质时也可以把ε,µ写成非线性函数,当然媒质参数也可以是随时间变化的函数.介电常数也可以是位置的函数,即表征空间媒质的非均匀性.本文研究的重点是ε,µ是频率的复杂函数的情形.色散媒质能更好的描述现实世界,因此我们有必要对色散媒质的FDTD方法展开研究.为了仿真色散媒质,研究者们提出了多种色散模型,比如Debye,Drude,Lorentz以及Drude-Lorentz模型[6−8].
辛时域有限差分算法(SFDTD)[9−11]在稳定性,长时间迭代以及色散误差等方面比普通FDTD算法有很大的优势.构造SFDTD算法需要将包含媒质参数的Maxwell方程写成矩阵形式,在计算时间演化矩阵exp(∆tL)时,要求L分裂成的两个矩阵U,V满足矩阵指数exp(cl∆tU),exp(dl∆tV)收敛. 但是由于色散媒质的电磁参数相对复杂,使得矩阵U,V的构造相当困难.文献[12]对无耗散项的Drude模型构造了SFDTD算法.针对更具有普遍意义的有耗散项Drude-Lorentz模型,本文建立了可以处理双色散模型的SFDTD算法.
2 理论和数值推导
2.1 Drude-Lorentz色散模型的辛算法框架
Drude模型是比较常用的色散模型,它可以很好地拟合一些材料的电磁参数,有时候为了进一步提高对材料电磁参数的拟合,需要引入Lorentz修正项,即通过Drude和Lorentz模型的叠加来提高拟合的精度.此时复的相对介电常数ε及复的相对磁导率µ可表示为
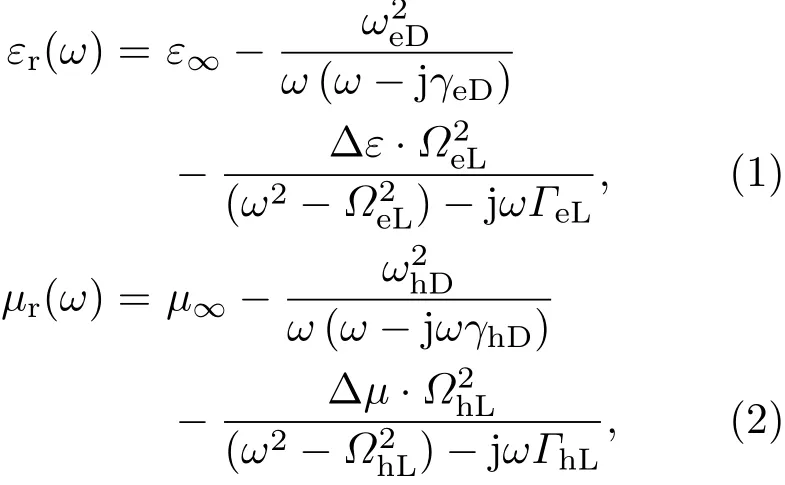
其中,ε∞及µ∞分别为无限频率的相对介电常数和相对磁导率,ωeD和ωhD分别为电等离子体角频率和磁等离子体角频率,γeD及γhD分别为电碰撞频率和磁碰撞频率,∆ε及∆µ为引入Lorentz修正项后介电常数及磁导率的相对改变量,ΩeL及ΩhL为非损耗谐振频率,ΓeL及ΓhL是损耗系数.为简单起见,这里只考虑一项修正,对于多项修正可类推.
无耗,各项同性,均匀介质空间中的Maxwell方程组的频域形式为
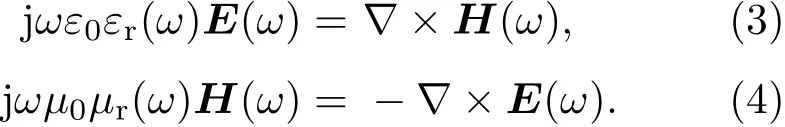
考虑到本构关系,引入如下辅助变量:
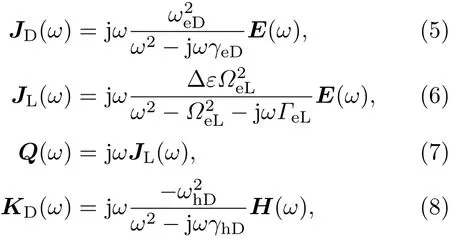

因此,(3),(4)式可改写为
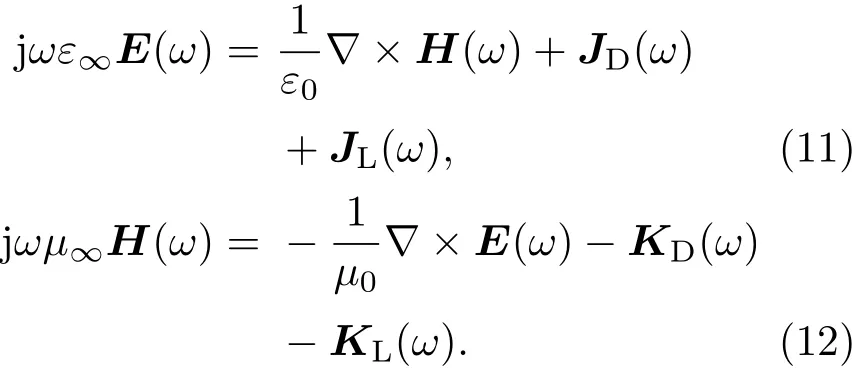
结合逆傅里叶变换,(5)–(12)式对应的时域形式为
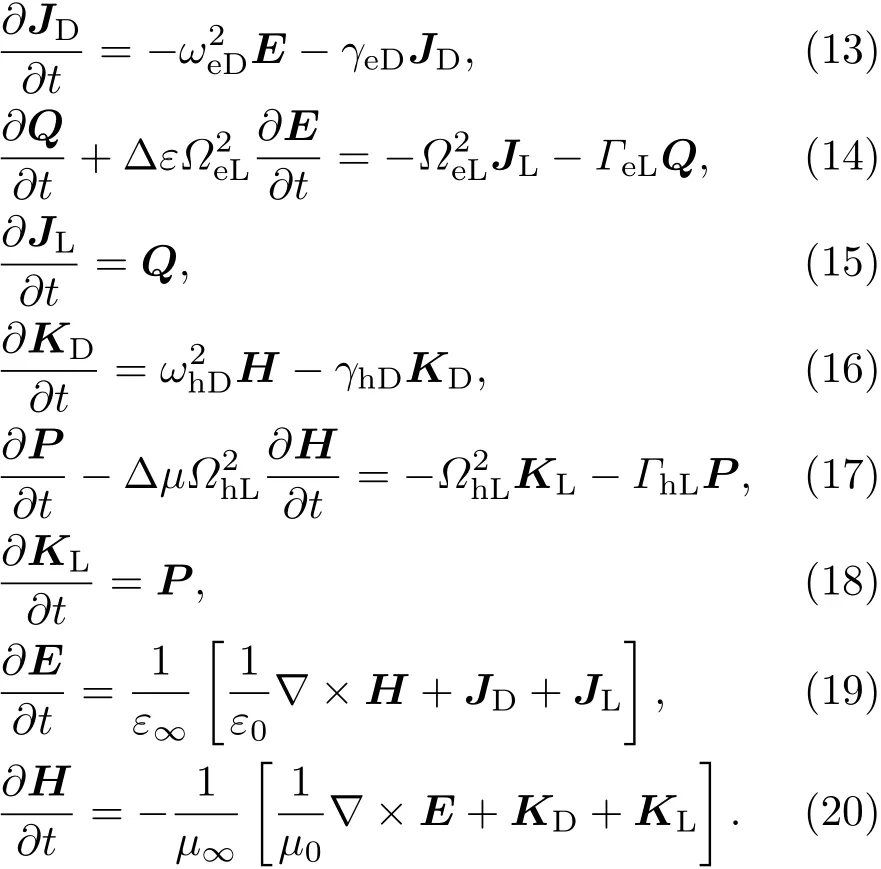
方程(13)–(20)可进一步改写成矩阵形式

其中,G=(H E KLJLP Q KDJD)T,
(1)科教部门负责科研经费的管理,负责审核和控制各项科研经费的支出。各专项科研经费划拨我院后,科研科根据医院文件规定,分级别按比例给予匹配一定的经费,并按项目负责人立户,一题一本(科研经费使用记录本),标明项目名称、项目负责人、允许使用经费的额度。


方程(21)可表示为

其中,

为简化记号,引入

引入辛算法近似,考虑时间步进从t=0到t=∆t,结合(24)式有
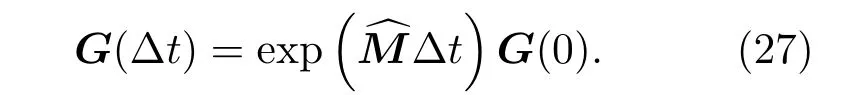


考虑到U及V不可交换性,利用基本辛矩阵的乘积,矩阵算符可近似为
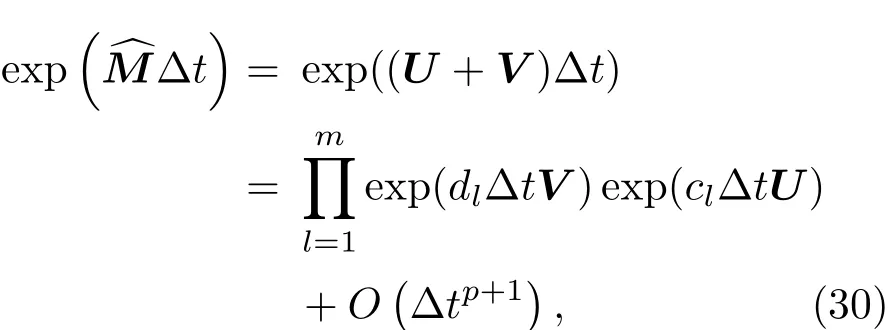
其中,对应参数的定义与普通辛算法一致.尽管Uα≠0及Vα0(α ≥ 2),指数算符exp(dl∆tV)及exp(cl∆tU)可由表达式(31),(32)定义并计算:

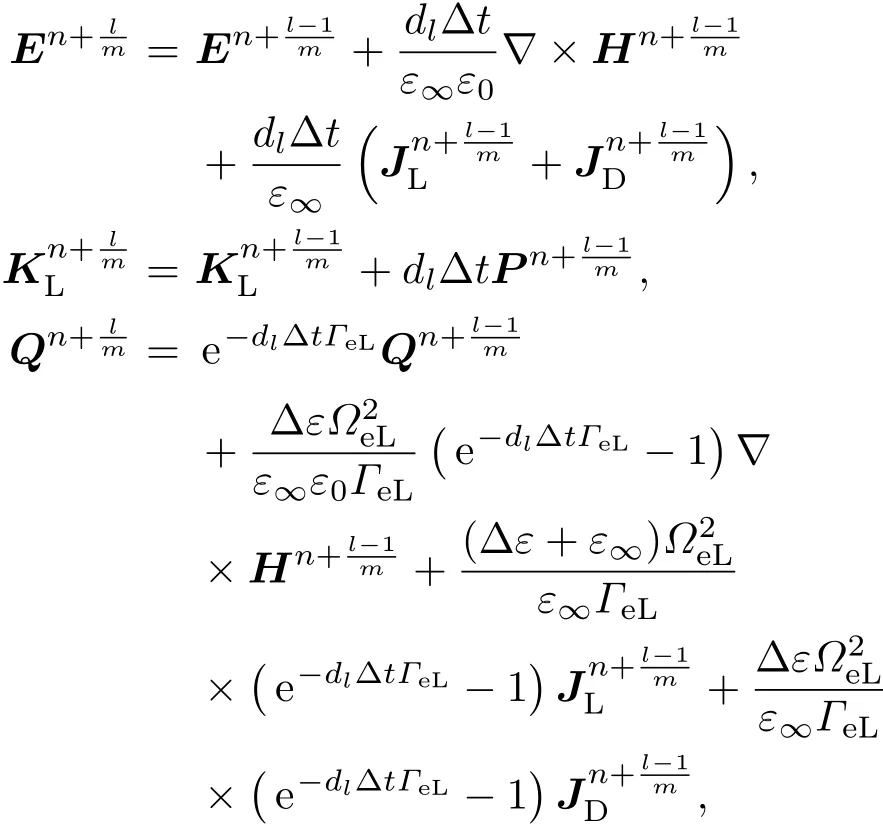
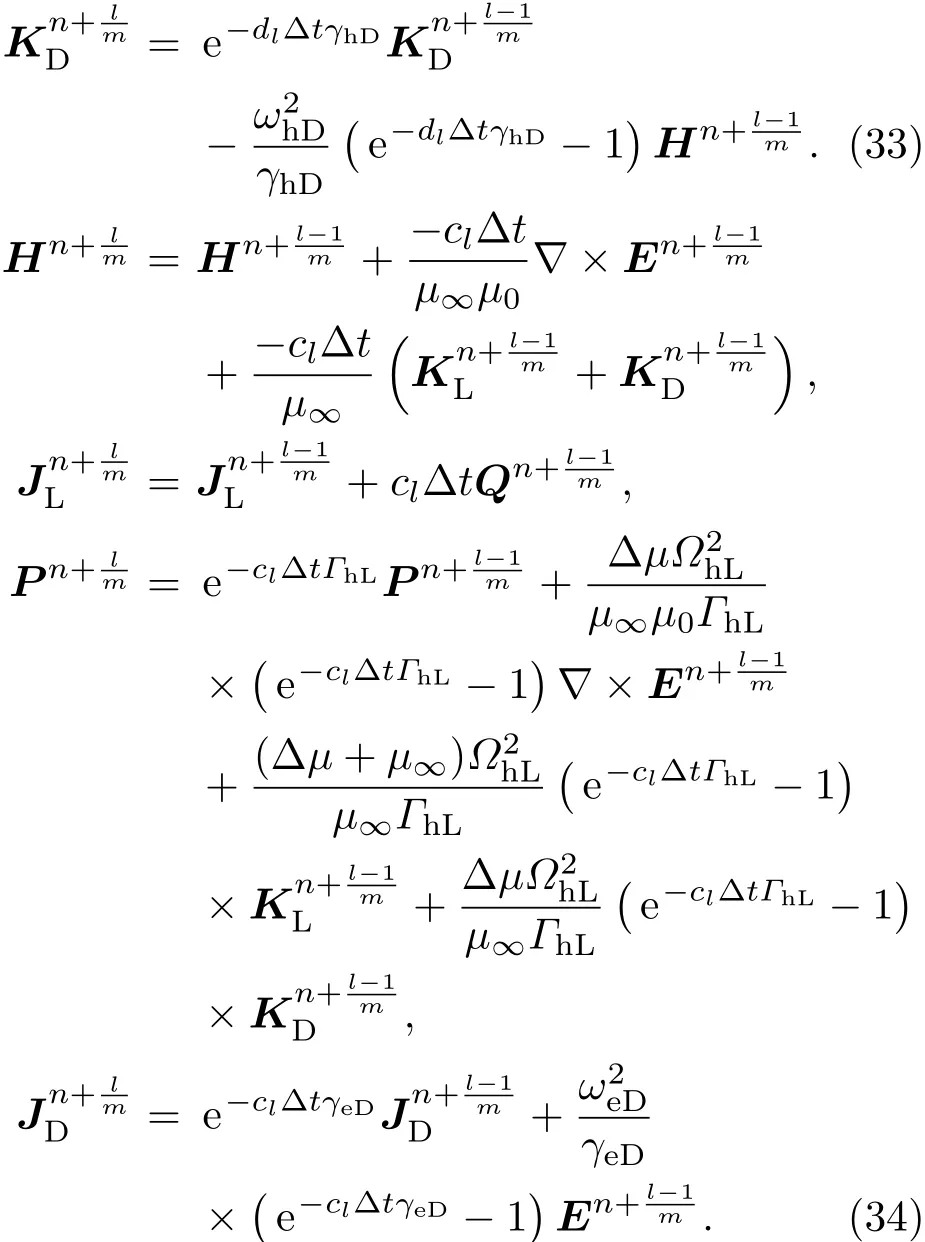
至于空间一阶偏导数的离散可借助于四阶交错差分,即

因而,结合时间及空间离散,最终建立了空间四阶时间任意阶的SFDTD算法以处理双色散媒质,而且本文构建的方法可以直接退化为单色散媒质及普通媒质的SFDTD算法.
3 数值算例
3.1 双色散平板模型的传输问题
为了验证本文方法的有效性,首先考虑平板的传输问题. 以结构为50 nm厚且为双色散材质的平板作为研究对象,参考贵金属金的相对介电常数,设置该平板的相对介电常数为一个Drude项加一个Lorentz修正项,其对应的参数分别为:ε∞=1.17152,∆ε=2.233994,γeD=3.21×1013rad/s,ωeD=1.37×1016rad/s,ΓeL=2π×6.22×1013rad/s及ωeL=2π×1.31×1015rad/s.另外设置该平板的相对磁导率与相应的相对介电常数相同,即 µ∞=1.17152,∆µ =2.233994,γhD=3.21× 1013rad/s,ωhD=1.37×1016rad/s,ΓhL=2π×6.22×1013rad/s,ωhL=2π×1.31×1015rad/s,为了对SFDTD和普通FDTD算法进行比较,计算区域设为300 nm,平板置于计算区域的中心,最外层为20个网格的PML,入射的平面波源为调制的高斯激励
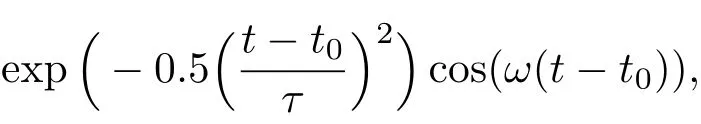
其中 ω =4π×1014rad/s,τ=5.0×10−15s,t0= τ,其他相关计算参数见表1.图1给出了该平板在125–275 THz频段透射系数的精确解,SFDTD解以及普通FDTD解.由图1可以看出SFDTD(红色圆点),FDTD(黑色三角形)和精确解(蓝色实线)的误差相当.表1给出了两种算法结果对应的内存以及计算时间的比较.由表1可以看出,在相同精度下,SFDTD可以设置较大的稳定性系数以及网格步长,从而可以减少计算时间.结果证明本文建立的Drude-Lorentz双色散模型的辛算法框架是有效的.
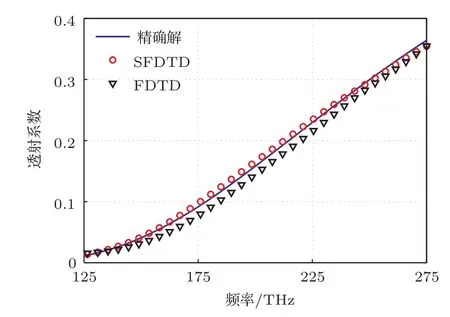
图1 (网刊彩色)透射系数比较
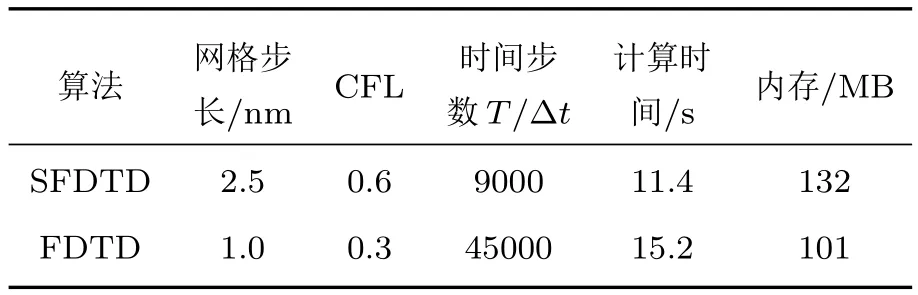
表1 算法性能比较
3.2 三维U形开口谐振环(SRRs)的特性分析
U形SRRs环具有周期性结构,它在开关,传感器等方面有着广泛的应用.作为第二个例子,利用本文构建的色散模型SFDTD算法,计算分析U形SRRs环的透射系数,反射系数以及吸收系数.U形SRRs环结构如图2所示,该结构在x,y方向上是周期,且是周期长为p=250 nm的正方形结构.其他结构参数为a=150 nm,w=50 nm,d=75 nm,hg=60 nm,hs=40 nm.下层蓝色区域为介质基板(GaAs材料介电常数εr=11.0);上层黄色区域为贵金属银,考虑到研究的波长范围为[1200,2400]nm,用一个Drude项拟合银在该波段的介电常数,其相应的Drude参数为ε∞=1.0,ωeD=1.37×1016rad/s,γeD=2.73×1013rad/s.电磁波垂直于SRRs平面入射,其电极化方向平行于y轴,z方向上设置15层厚度的高阶分裂场PML作为吸收边界.图3是仿真后得到的透射系数(黑色实线),反射系数(蓝色实线)和吸收系数(绿色实线),而且给出了FDTD算法结果的对比.表2是SFDTD和FDTD计算参量的对比,可以看出,由于SFDTD算法可以将CFL以及网格步长设置的较大,从而在计算时间和内存上比FDTD占优.
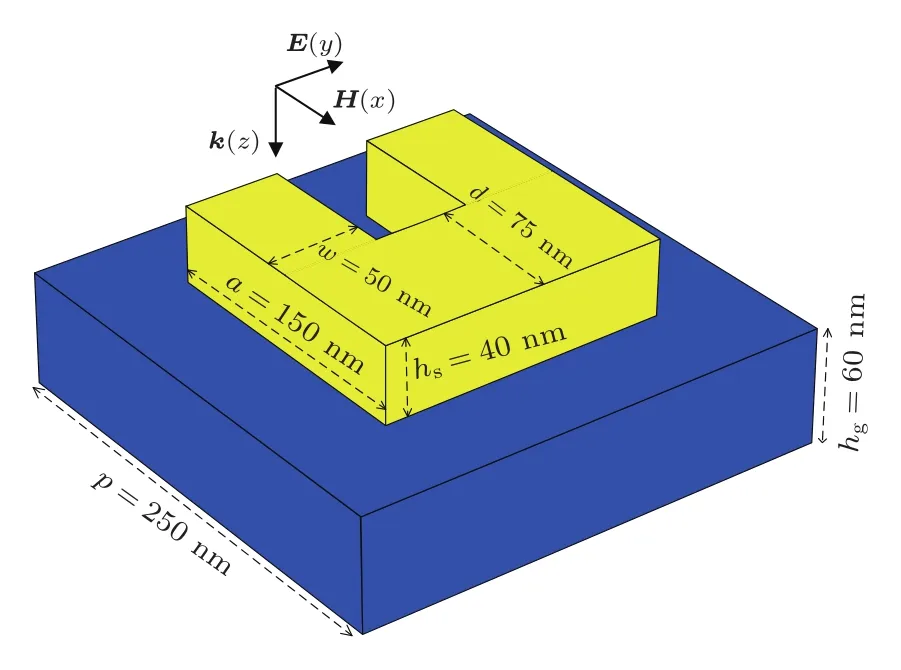
图2 (网刊彩色)SRRs结构示意图
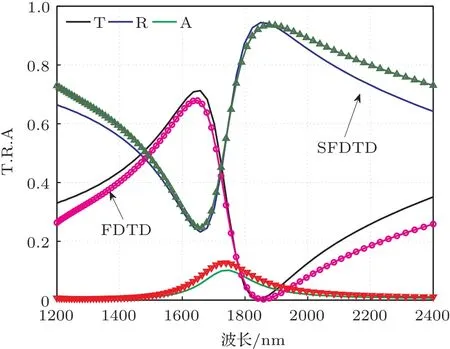
图3 (网刊彩色)垂直入射时SRRs结构的透射系数,反射系数和吸收系数
图3中,根据透射系数的变化可以看出该SRRs结构的谐振频率对应的波长位于1850 nm附近,吸收峰位于1740 nm附近.
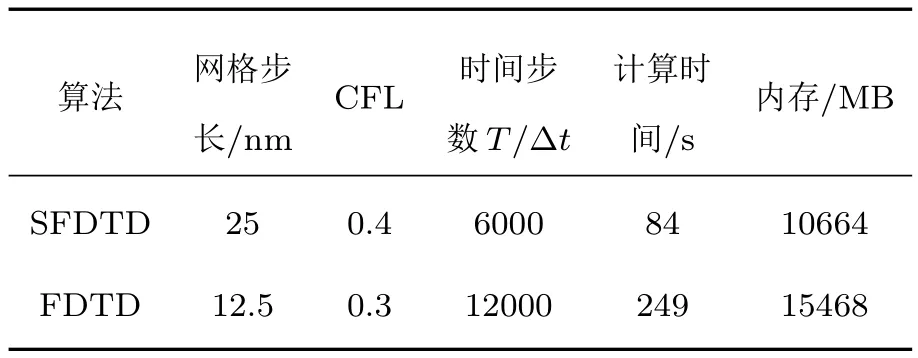
表2 算法性能比较
4 结 论
SFDTD算法是一种能量守恒,条件稳定且能得到宽频带特性的有效数值方法,本文基于矩阵分裂,辛算子技术以及ADE方法构建了Drude-Lorentz电磁双色散模型的辛算法框架,该算法在时间上为任意阶,可以灵活处理.通过严格的公式推导,得到了一个Drude和一个Lorentz项叠加的双色散模型的SFDTD算法迭代公式,对于多个Drude或者Lorentz项叠加的色散模型,需要引入更多的中间变量,可以类似推导.数值仿真结果证明了构建的双色散模型的SFDTD算法的可行性和有效性.该算法为色散材料的研究提供了有力的算法支持.
附录A 矩阵指数展开
以(32)式为例,下面可以证明其展开后的计算结果是收敛的,展开后矩阵指数的收敛这是本文构建的算法的基础.矩阵U的表达式为(28)式,根据矩阵的乘法运算,可以得到任意整数个U矩阵乘积的结果:



令
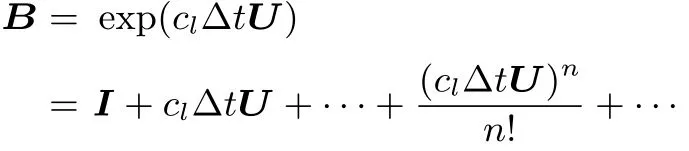
其中I为单位阵.那么B矩阵中的非零元素可计算得到
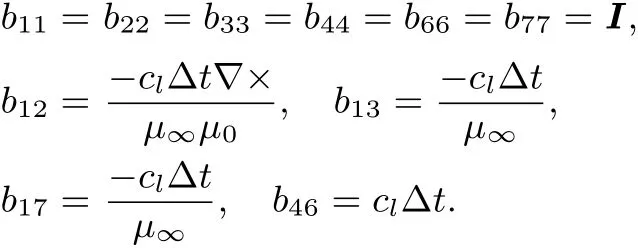
简单记α=cl∆t,于是
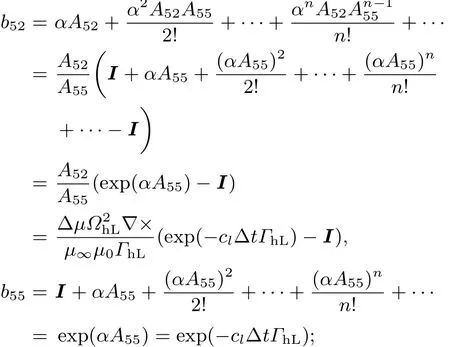
同样可以得到
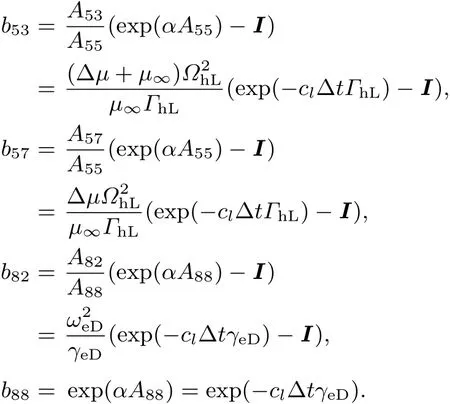
[1]Ai F,Bai Y,Xu F,Qiao L J,Zhou J 2008 Acta Phys.Sin.57 4189(in Chinese)[艾芬,白洋,徐芳,乔利杰,周济2008物理学报57 4189]
[2]Liu R,Shi J H,Plum E,Fedotov V,Zheludev N 2012 Acta Phys.Sin.61 154101(in Chinese)[刘冉,史金辉,E.Plum,V.A.Fedotov,N.I.Zheludev 2012物理学报61 154101]
[3]Wang W S,Zhang L W,Ran J,Zhang Y W 2013 Acta Phys.Sin.62 184203(in Chinese)[王五松,张利伟,冉佳,张冶文2013物理学报62 184203]
[4]Ta flove A,Hagness S C 2005 Computational Electrodynamics:The Finite-Difference Time-Domain Method,third ed.(Boston:Artech House)
[5]Sullivan D M,Hagness S C 2005 Electromagnetic Simulation Using the FDTD Method(New York:IEEE Press)
[6]Prokopidis K P,Tsiboukis T D 2007 Appl.Comput.Eletron.22 287
[7]Deinega A,John S 2012 Opt.Lett.37 112
[8]Vial A,Grimault A-S,Macías D,Barchiesi D,Chapelle M L 2005 Phys.Rev.B 71 085416
[9]Sha W,Huang Z X,Chen M S,Wu X L 2008 IEEE Trans.Antennas Propag.56 493
[10]Hirono T,Lui W,Seki S,Yoshikuni Y 2001 IEEE Trans.Microw.Thory Tech.49 1640
[11]Wang H,Huang Z X,Wu X L,Ren X G 2011 Chin.Phys.B 20 114701
[12]Ren X G,Huang Z X,Wu X L,Lu S L,Wang H,Wu L,Li S 2012 Comput.Phys.Commun.183 1192
