钢轨吸振器对高架结构垂向振动的影响

杨建近，杨新文

（1.兰州交通大学 机电工程学院，兰州730070；2.同济大学 交通运输工程学院，上海201804）

钢轨吸振器对高架结构垂向振动的影响

杨建近1，杨新文2

（1.兰州交通大学 机电工程学院，兰州730070；2.同济大学 交通运输工程学院，上海201804）

建立带有钢轨吸振器的高速铁路高架结构板式轨道与桥梁垂向耦合振动模型，分析钢轨吸振器对轨道和桥梁结构垂向振动的影响。模型已考虑了钢轨吸振器、板式轨道结构及桥梁间的耦合作用。钢轨吸振器被视为两自由度的质量—弹簧系统，钢轨、轨道板和桥梁被视为多层叠合梁模型，彼此用弹簧阻尼元件联接。利用动柔度函数，得到吸振器—板式轨道—桥梁系统垂向振动响应的解析表达式，并以轮轨表面粗糙度谱作为激励求解模型的振动响应。研究结果表明：钢轨吸振器在180 Hz～300 Hz及700 Hz～1 000 Hz频段内对整个高架轨道系统的位移幅值及相位、振动衰减产生较明显的影响；同时，在轮轨表面粗糙度谱的激励下，带有钢轨吸振器的轮轨系统的轮轨力在pinnedpinned频率处明显减小，在前两阶自振主频附近钢轨吸振器对整个高架轨道系统结构振动的影响较明显。

振动与波；高速铁路；高架结构；钢轨吸振器；耦合振动；动柔度

上述研究中的轨下支承是由刚性基础上的扣件系统、轨枕和道砟组成，没有考虑与轨道板和板下结构的相互影响。而钢轨吸振器对钢轨振动产生的影响，一方面使钢轨传递给轨下基础的能量发生变化，另一方面使作用在整个轨道系统上的轮轨力发生变化，从而对整个轨道系统的振动产生影响。那么钢轨吸振器对整个高架轨道系统的影响有多大呢？本文建立了钢轨吸振器—板式轨道—高架桥梁耦合动力学模型并以轮轨表面粗糙度为输入，来探究钢轨吸振器对整个高架结构的影响。

1 钢轨吸振器—板式轨道—高架桥梁耦合相互作用模型

1.1 物理模型

根据文献[3]将钢轨吸振器简化为质量—弹簧系统，离散地安装在钢轨上扣件跨中处，m2和m1分别为上下质量层的质量，质量层间的弹性阻尼材料用线性弹簧k1、k2和k3表示，损耗因子为ƞa。高架桥梁板式轨道结构主要由钢轨、扣件、轨道板、CA砂浆层及高架桥梁组成，建模时将钢轨视为无限长的具有垂向和截面转角运动自由度的Timoshenko梁，轨道板用两端自由的具有垂向运动自由度的Euler梁模拟，桥梁用简支的具有垂向运动自由度的Euler梁模拟。扣件、CA层和桥梁支座用离散的线性弹簧kf、kj和kz表示，损耗因子为ƞf、ƞj和ƞz。根据轨道结构系统动力学理论建立钢轨吸振器—轨道板—高架桥梁相互作用耦合模型，如图1。

1.2 钢轨吸振器—板式轨道—高架桥梁运动方程

运动微分方程为

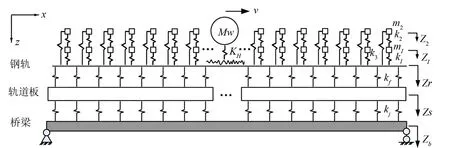
图1 钢轨吸振器—板式轨道—高架桥梁相互作用耦合模型

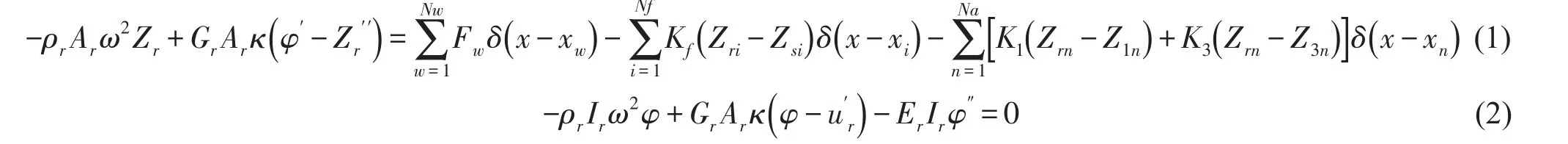
其中Zr、φ分别为钢轨垂向位移和截面转角，Nw、Nf和Na分别为激励、扣件和吸振器的数量，xw、xi和xn分别为第w个激励的坐标、第i个扣件的坐标和第n个吸振器的安装位置；Zrn、Z3n和Z1n分别为钢轨和吸振器上下质量层在坐标xn处的垂向位移，Zri、Zsi分别为钢轨和轨道板在坐标xi处的垂向位移，Ir、Ar、ρr、Gr、Er和κr分别为钢轨的截面惯性矩、横截面面积、密度、剪切模量、弹性模型和剪切系数，Fw为激励，ω为激励的角频率。“’”表示对位置坐标的微分。

根据虚位移原理，钢轨吸振器的运动微分方程为

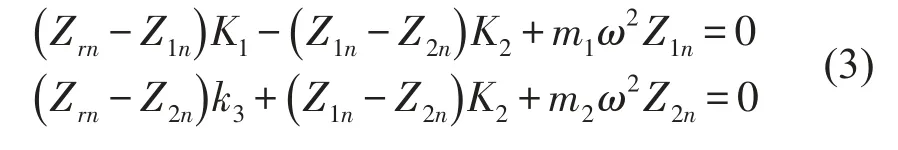
由式（3）可得

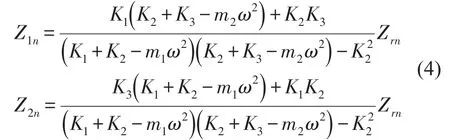
将式（4）带入式（1），得

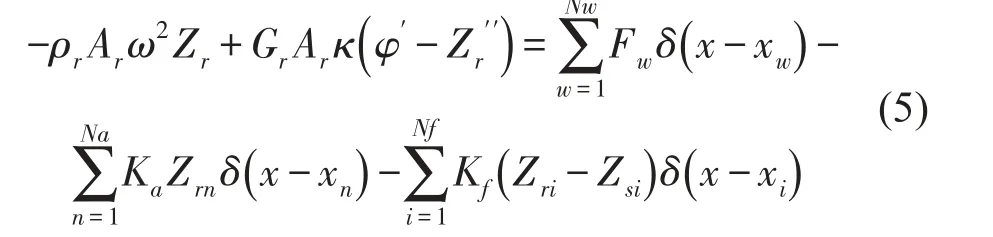
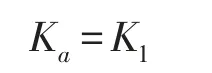
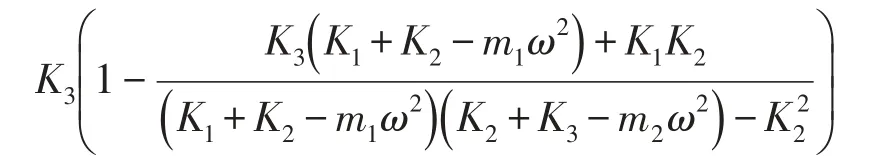
钢轨的运动微分方程可写为

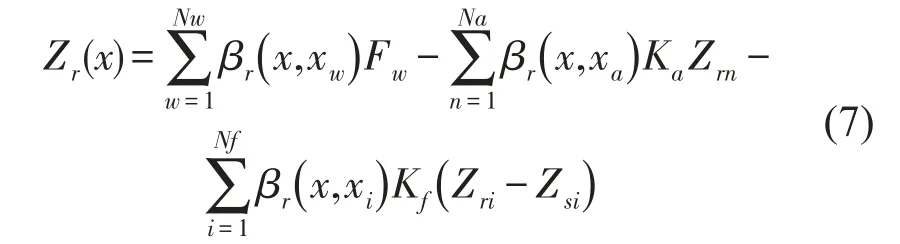
其中βr(x1,x2)为钢轨的无限长Timoshenko梁模型的动柔度[7]，表示在x2处施加单位简谐力钢轨在x1处的位移。Kf(Zri-Zsi)为第i个扣件的弹性恢复力。

多个轨道板的动柔度可表示为βs(x1,x2)=diag[ [βs1]1,…，[βs1]m，…，[βs1]M]，βs1为一块轨道板的两端自由Euler梁模型的动柔度[8]，M为轨道板数量，则整个轨道板的运动微分方程为

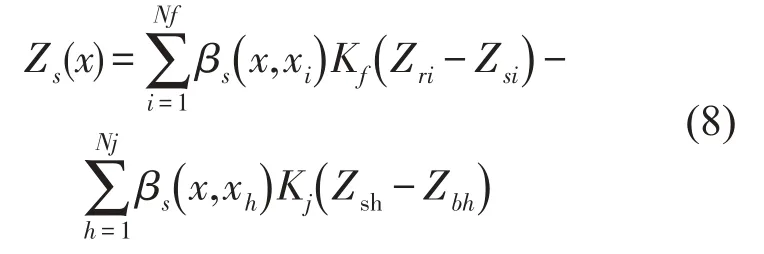
其中Nj为轨道板下离散分布弹性支承的数量，xh为轨道板下第h个离散分布弹性支承点的坐标，Zsh、Zbh分别为轨道板和桥梁在坐标xh处的垂向位移，Kj(Zsh-Zbh)为第h个离散支撑的弹性恢复力。

高架桥梁的运动微分方程为

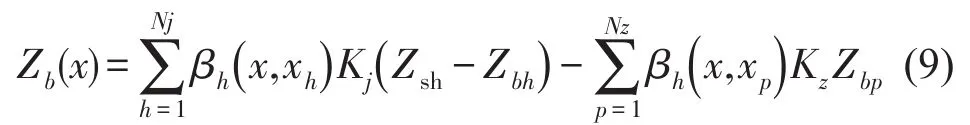
其中βh(x1,x2)为高架桥梁的简支Euler梁模型的动柔度[9]，Nz为高架桥梁支撑的数量，xp为高架桥梁第p个支撑的坐标，Zbp为桥梁在xp处的位移。KzZbp为高架桥梁第p个支撑的弹性恢复力。

上述公式中均未明示阻尼，实际上梁的弯曲刚度以及弹簧的刚度都是包含损耗因子的复刚度。将式（7）—（9）合并，可得到矩阵形式的表达式

[βK]主要由钢轨、轨道板和桥梁结构的动柔度乘以刚度以及钢轨的动柔度乘以Ka形成的；{u}由待求解的钢轨、轨道板和桥梁结构的位移组成。{F}为荷载矩阵。求解式（10）即可以得出，激励作用下安装有钢轨吸振其的高架轨道结构的频域位移响应；而当施加单位简谐力时，所求得出的位移响应就是高架轨道结构的导纳函数，同时也可以求出在轨道结构任意点处施加荷载时，轨道结构任意一点处的位移导纳函数。

2 数值分析

在理论计算分析中，采用6块CRTS-I型4.962 m长标准轨道板[10]，轨道板的损耗因子为0.05；采用60 kg/m钢轨的参数，损耗因子为0.01，其他计算参数如表1。

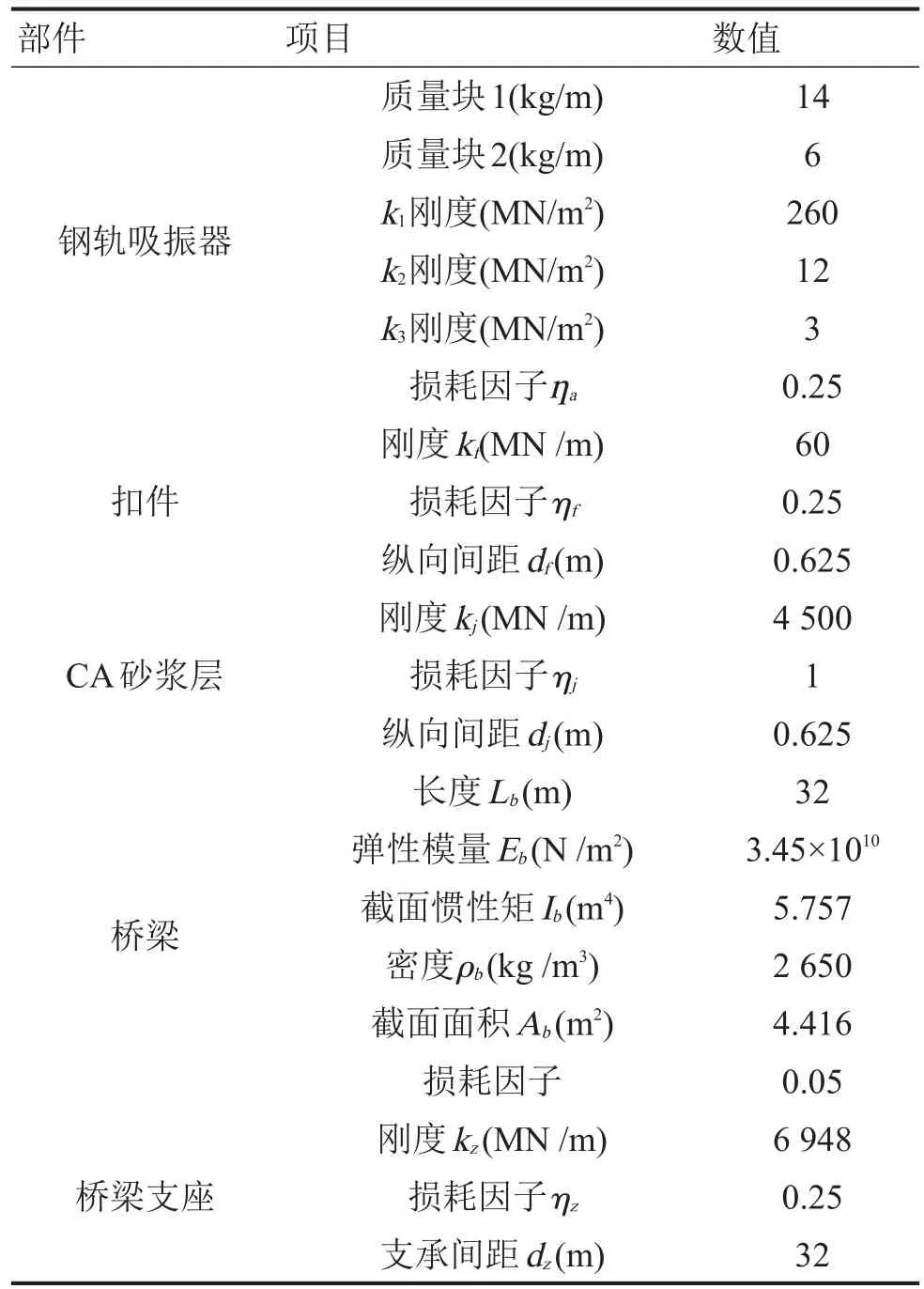
表1 模型的计算参数

2.1 系统结构导纳特性分析

结构导纳是指结构在受到单位力作用时各部位产生的位移，又称为结构动柔度，一般为复数形式，用其幅频和相频曲线来反映结构响应的传递规律。结构振动衰减率用来表示结构上随着距离激励点距离改变振动衰减的特性，定义为

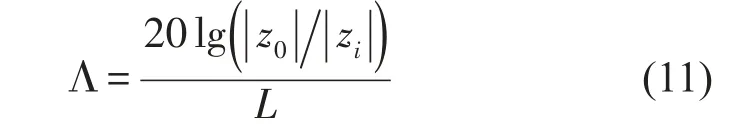
式中z0为激励点处结构振动位移，zi为距离激励点L处结构振动位移。

为了分析安装有钢轨吸振器的高架轨道结构系统的结构导纳特性，以单跨32 m高速铁路简支箱梁高架轨道系统为研究对象，在桥梁跨中截面的钢轨上（扣件跨中）施加单位简谐荷载，以1 Hz为步长计算系统的导纳。由于桥梁跨中截面位于两个轨道板间的间隙中，故取靠近桥梁跨中截面扣件下的轨道板的位移导纳及桥梁跨中截面上钢轨和桥梁的位移导纳为研究对象。分别在钢轨、轨道板和桥梁上沿钢轨方向取距离上述点L=6.25 m处结构的振动分析振动在高架轨道系统中的纵向衰减。图2给出了钢轨吸振器对高架轨道系统各结构的位移导纳幅值、位移导纳相位和振动衰减的影响。

从图2可知钢轨吸振器在180 Hz～300 Hz及700 Hz～1 000 Hz频率内对整个高架轨道系统的位移导纳特性和振动衰减产生较明显的影响，其他频段对高架轨道系统几乎不产生影响，这是由于钢轨吸振器的前两阶共振频率分别在250 Hz左右和700 Hz左右。

在高架轨道系统位移导纳变化方面，钢轨吸振器使钢轨在230 Hz左右（钢轨—扣件系统的自振频率）的峰值减小，由于安装吸振器使钢轨的质量增大，导致其这个峰值对应的频率前移到200 Hz左右，还钢轨振动在第一个pinned-pinned频率的峰值明显减小；使轨道板在200 Hz～300 Hz及750 Hz左右的位移导纳幅值减小；使高架桥梁在200 Hz～300 Hz的位移导纳幅值略微减小，在700 Hz～1 000 Hz的位移导纳幅值变化趋于缓和。

在高架轨道系统位移导纳相位变化方面，桥梁的位移导纳相位变化最复杂，特别是在1 000 Hz以上的高频段在正值与负值间交替出现峰值，轨道板的次之，钢轨的最简单。而钢轨吸振器使钢轨的位移导纳相位在pinned-pinned频率处发生较明显的变化；使轨道板的位移导纳相位在200 Hz左右突变出现了明显的正负值峰值交替；总体上没有改变桥梁位移导纳相位变化的趋势，只使桥梁位移导纳相位在700 Hz～1 000 Hz的变化趋于缓和。

在高架轨道系统位移导纳衰减方面，钢轨振动的衰减率变化较简单，轨道板和桥梁的振动衰减率变化较复杂，钢轨振动在1 000 Hz以下衰减较明显而在1 000 Hz以上高频段钢衰减较小；钢轨吸振器使钢轨振动在700 Hz～800 Hz的衰减明显增大而出现峰值，而使轨道板及桥梁振动在750 Hz左右的衰减减小。

2.2 粗糙度谱激励下系统振动响应分析

当车轮以一定速度在钢轨上运行时，在轮轨表面组合粗糙度激励下，车轮和钢轨会通过接触面产生轮轨耦合动态作用力，从而使高架轨道系统产生振动。轮轨耦合动态垂向作用力可表示为[11]

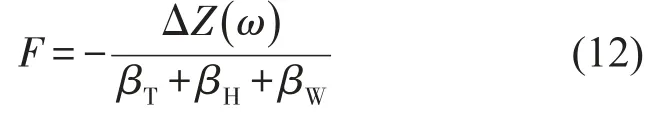
式中ΔZ(ω)为包含轮轨接触滤波效应的车轮和钢轨表面组合粗糙度谱，上凸为负下凹为正；βT为轨道系统在轮轨接触点处的原点垂向位移导纳，由式（10）可求得；βH为轮轨接触的动柔度，βH=1/kH，kH为轮轨接触刚度选取1 140 MN/m；βW为车轮在接触点处的位移导纳，可近似表示为[11]

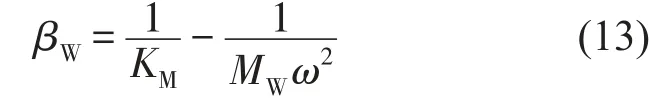
KM和MW分别为车轮弹簧—质量模型的弹簧刚度和质量，取值为KM=4 390 MN/m，MW=840 kg。

由于我国对高铁的研究起步较晚，尚没有能反映我国高铁轮轨表面特征的组合粗糙度谱，计算中采用国外文献中给出的一组考虑轮轨接触滤波效应的轮轨组合粗糙度谱[12]，如图3。

利用式（12）计算有无钢轨吸振器情况下的轮轨垂向动态作用力，再利用式（10）计算轮轨力作用下高架轨道系统结构垂向振动。图4和图5为有无钢轨吸振器时，车轮速度为200 km/h时粗糙度激励下的动态垂向轮轨力幅值和高架轨道系统结构振动响应。

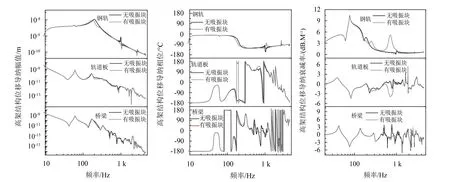
图2 钢轨吸振器对高架轨道系统结构垂向振动的影响

由图4可以看出，无钢轨吸振器时轮轨力在75 Hz(对应波长的0.740 7 m)和1 015 Hz(对应的轮轨组合粗糙度波长为0.054 7 m)处出现了两个明显的峰值，而钢轨吸振器使后一个峰值明显的减小了，而使轮轨力在250 Hz左右稍有增加。由图5可以看出，钢轨吸振器使钢轨在前两个pined-pined频率处的加速度幅值明显降低，对其他频率的钢轨加速度幅值无明显影响；使轨道板的加速度幅值在200 Hz左右、577 Hz左右和842.3 Hz左右的峰值减小，其他频率上钢轨吸振器几乎不对轨道板加速度幅值产生影响；使高架桥梁的加速度幅值在200 Hz左右、520 Hz～750 Hz左右减小，其他频率上钢轨吸振器几乎不对高架桥梁的加速度幅值产生影响。从振动的角度考虑，轨道板和高架桥梁的振动主要是低频振动，故200 Hz以上钢轨吸振器对轨道板和高架桥梁振动的影响几乎可以忽略，但探究吸振器对轨道板和高架桥梁在200 Hz以上频段的影响，对研究高架轨道系统的结构全频段噪声辐射特性是有益的。

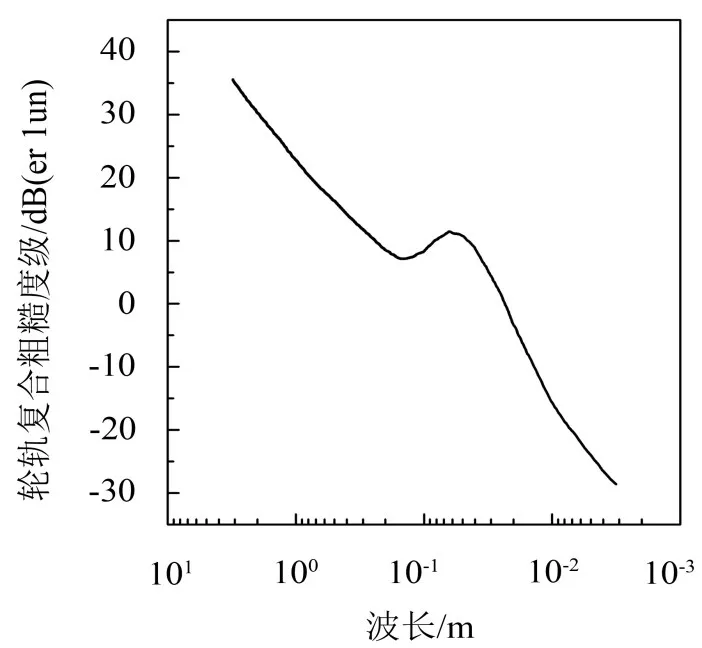
图3 轮轨组合粗糙度谱(考虑接触滤波的影响)

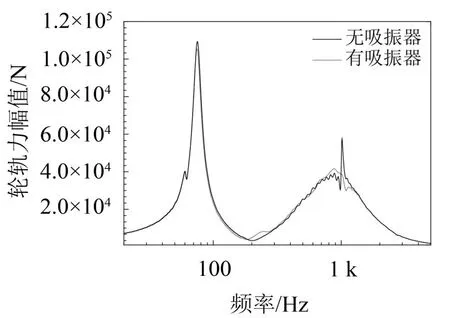
图4 粗糙度激励下的轮轨力

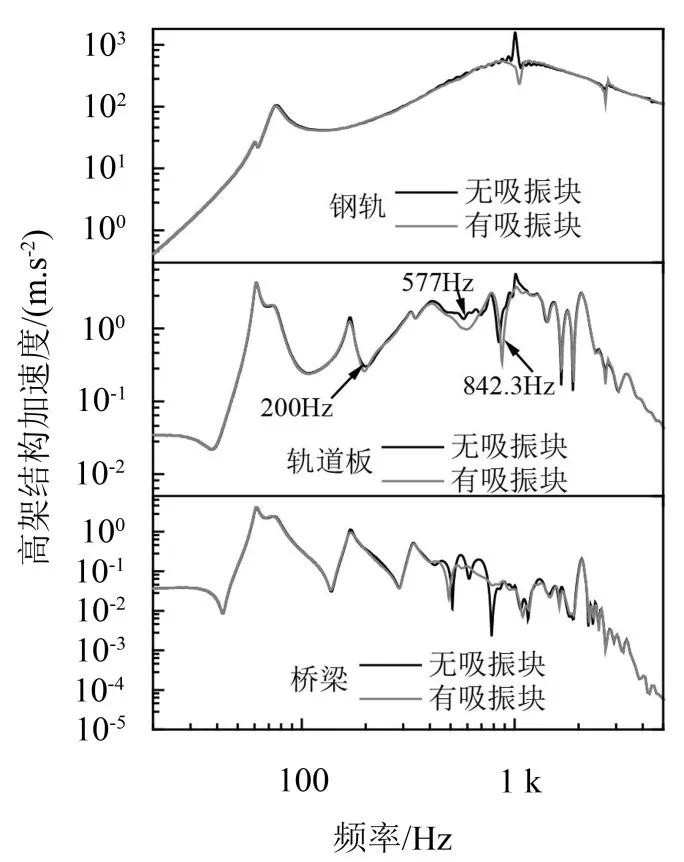
图5 粗糙度激励下轨道结构振动响应

3 结语

（1）钢轨吸振器在180 Hz～300 Hz及700 Hz～1 000 Hz频率内对整个高架轨道系统的位移幅值和相位、振动衰减产生较明显的影响，其他频段对高架轨道系统几乎无影响。总体上，对钢轨的振动影响最大，轨道板次之，桥梁最小；

（2）在轮轨表面组合粗糙度谱激励下钢轨吸振器使轮轨力在钢轨pinned-pinned频率明显减小，其他频段对钢轨力的影响较小；在吸振器前两阶自振主频附近，对整个高架轨道系统结构振动的影响较明显。

[1]杨新文，翟婉明，和振兴.高速列车运行产生的轮轨噪声预[J].噪声与振动控制，2011，31(3)：89-94.

[2]刘 震，刘林芽.无砟轨道钢轨导纳特性的实验研究[J].噪声与振动控制，2012，32(3)：78-81.

[3]Thompson D.J.,Jones C.J.C.,Waters T.P.,etc.A tuned damping device for reducing noise from railway track[J].Applied Acoustics,2007,68(1):43-57.

[4]T.X.Wu.Theoretical study on noise reduction of rail component by use of rail absorber[C].Proceedings of the 9 th International Workshop on Railway Noise,Munich, Germany,September 2007,4-8.

[5]T.X.Wu.On the railway track dynamics w ith rail vibration absorber for noise reduction[J].Journal of Sound and Vibration,2008,309(3):739-755.

[6]Liu H.P.,Wu T.X.,Li Z.G.Theoretical modelling and effectiveness study of rail vibration absorber for noise control[J].Journal of Sound and Vibration,2009,323(3-5):594-608.

[7]Carlone L,Thompson D J.Vibration of a rail coupled to a foundation beam through a series of discrete elastic supports[R].ISVR,University of Southampton,2001.

[8]翟婉明.车辆—轨道耦合动力学[M].北京：科学出版社，2007.

[9]Hamet J.F.Railway noise:use of the Timoshenko model in rail vibration studies[J].Acta Acustica united w ith Acustica,1999,85(1):54-62.

[10]王其昌，韩启孟.板式轨道设计与施工[M].成都：西南交通大学出版社，2002.

[11]WU T.X.,Thompson D.J.Vibration analysis of railway track w ith multiple wheels on the rail[J].Journal of Sound and Vibration,2001,239(1):69-97.

[12]Dings P.C.,Dittrich M.G.Roughness on Dutch railway wheels and rails[J].Journal of Sound and Vibration,1996, 193(1):103-112.

Effect of Rail Vibration Absorbers on Vertical Vibration of Elevated Structures

YANG Jian-jin1,YANG Xin-wen2

(1.School of Mechatronic Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China; 2.School of Transportation Engineering,Tongji University,Shanghai 201804,China)

The frequency-domain analysis model w ith a rail vibration absorber is established for analyzing the elevated slab-track and track-bridge coupled vertical vibration.The effect of the rail vibration absorber on the vertical vibrations of elevated railway and bridge is analyzed.The coupling effect of the absorber,rail,slab track and elevated bridge is considered.The absorber is modeled to be a mass-spring system w ith two degrees of freedom.The rail,slab track and elevated bridge are respectively considered as an infinitely long Timoshenko beam,an end-free Euler beam and a simply supported Euler beam,and they are connected one another w ith spring and damping elements.The vertical vibrations of the system are solved by dynamic flexibility functions.The effect of the absorber on the vertical vibration of the elevated railway is analyzed,and the vibrations of the elevated railway structures excited by the wheel-rail roughness spectra are obtained.The results show that,the absorber has a significant effect on the vibration decay and displacement amplitude and phase of the whole structures of the elevated railway in the frequency ranges of 180 Hz～300 Hz and 700 Hz～1 000 Hz.Under the excitation of wheel/rail roughness spectra,the absorber can reduce the wheel/rail force obviously at the“pinnedpinned”frequency of the rail and has an obvious effect on the whole structure of the elevated railway around its first and second order natural frequencies.

vibration and wave;high speed railway;elevated railway;rail vibration absorber;coupled vibration; dynam ic flexibility function

1006-1355(2014)04-0214-05

TB53；U211.5；U213 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.047

在高速铁路运行过程中，轨道结构的振动会引起高架轨道的高架桥结构振动或地面振动，由此对线路沿线的建筑产生危害，也会因隨之激励的噪声对沿线产生环境污染。尤其是在我国的高速线路中，大量采用的是板式轨道结构，在高速列车的作用下轨道结构的振动及噪声辐射会加剧[1，2]。针对轨道结构采取减振措施，能够从源头上控制高速铁路引起的结构振动。2006年，D.J.Thompson等[3]提出了一种主要由质量块和弹性阻尼层组成的钢轨吸振器，一般将其对称地安装在钢轨两侧，它能有效的降低钢轨的振动，并使钢轨的噪声辐射降低6 dB左右。吴天行[4，5]将钢轨吸振器简化为两自由度的质量—弹簧装置并对其进行参数分析及改变安装位置，分析了其减振降噪的机理及效果，得到了将其安装在钢轨上轨枕跨中位置能够最大限度的降低钢轨的振动及噪声辐射的结论。刘海平等[6]将较长的吸振器简化为自由—自由边界的有限长Euler-Bernoulli梁，建立了更精确的有砟轨道—吸振器系统一维弹簧—梁力学模型，得到钢轨和吸振器任意位置的振动位移和弹性恢复力。

2014-03-03

国家自然科学基金资助项目（51165017）

杨建近（1988-），男，安徽蒙城人，硕士生，主要研究方向：轨道交通系统动力学。

杨新文（1973-），男，副教授，工学博士。

E-mail:xinwenyang@tongji.edu.cn