风力发电机弹性支承有限元分析

程 荣，温华兵，刘春岐，吕 珏，沈超明

（1.江苏科技大学 振动噪声研究所，江苏 镇江212003；2.镇江铁科橡塑制品有限公司，江苏 镇江212021；）

风力发电机弹性支承有限元分析

程 荣1，温华兵1，刘春岐2，吕 珏2，沈超明1

（1.江苏科技大学 振动噪声研究所，江苏 镇江212003；2.镇江铁科橡塑制品有限公司，江苏 镇江212021；）

橡胶材料的非线性力学特性直接影响到风力发电机弹性支承的减振性能。通过橡胶拉伸和压缩实验获得应力-应变数据，借助有限元软件对数据进行拟合，得到橡胶材料恰当的本构模型。依据弹性支承的实际使用工况，选用合理的橡胶材料模型参数，采用整体、四分之一截面和轴对称的三种模型进行计算结果的对比分析。并针对用四分之一模型分析风力发电机弹性支承的非线性垂向、横向刚度和固有频率等特性，通过试验；验证了有限元模型和计算方法的有效性。

振动与波；隔振；风力发电机；弹性支承；非线性；有限元分析

弹性支承是橡胶和金属材料的件，由于橡胶材料具有的高弹性和非线性特性，弹性支承的性能随着橡胶的配方比例、硬度、环境温度、受力状态等诸多因素而变化，以往是根据经验公式进行粗略计算[2]。但目前实现了对超弹性特性材料模型和体积近似不可压缩的有限元计算功能。本文主要对某型号风力发电机弹性支承进行静态非线性性能有限元仿真分析，并与实验结果进行对比，验证了非线性有限元模型的正确性，可为产品的设计开发提供指导。

1 橡胶本构模型研究

1.1 本构理论与模型

橡胶材料属于超弹性材料，应力-应变关系呈非线性，建立正确的橡胶材料的本构模型，是准确描述风力发电机弹性支承力学性能的关键因素。然而，对弹性体的非线性材料性质进行标定较为困难，其材料的本构关系用弹性应变能函数如下[3]

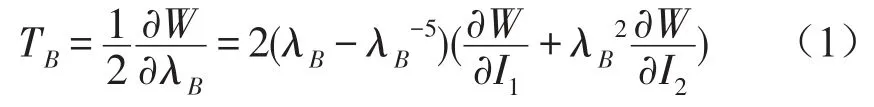
式中TB表示应力；W表示应变能函数；λB为主拉伸比；Ii(i=1,2)为主应变不变量。以应变能密度函数为基础，已发展出几种本构理论，它们适用于粘弹性材料的高弹性变形。这些本构方程分为两类。第一类假定应变能密度是主要应变常量的多项式函数。对不可压缩材料来说，材料模型一般指Rivlin材料。若只使用一次项，则指Mooney-Rivlin材料,其他模型还有Arruda-Boyce，Polynom ial等。第二类则假定应变能密度是三个主要拉伸的可分离的函数。所用模型有Ogden、Van der Waals、Peng-Landel材料模型。根据有限元软件对实验数据的拟合曲线发现，Readuced Polynom ial，N=1(Neo hooke)[2]模型较好的吻合弹性支承橡胶的应力应变关系，其模型应变能函数如下

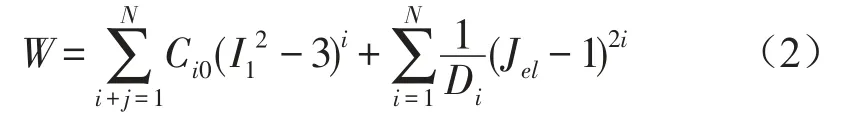
式中

N——材料参数,是温度的函数；

Ci0——材料参数，代表剪切特性，是温度的函数，根据实验数据回归；

Di——表示材料的可压缩性，材料参数，是温度的函数，根据实验数据回归；

I1=λ12+λ22+λ32，其中λ1，λ2，λ3为主伸缩比；

Jel=λ12λ22λ32

1.2 实验拟合结果

本文研究的风力发电机弹性支承所用的橡胶为天然橡胶和顺丁胶的混炼胶。由于实验条件的限制，只对橡胶材料进行了标准试片的单向拉伸和圆柱型试样的单向压缩试验。橡胶材料的应力应变试验在型号为CMT 6104的微机控制电子万能试验机上进行，图1为橡胶材料的拉伸试验。测试得到了硬度为45、50、58、64、73的橡胶应力—应变曲线。

实验数据以名义应力—应变的形式提供给有限元分析软件，利用其程序对材料进行评估，对预选的本构模型拟合应力—应变曲线。图2是对硬度为45的橡胶单轴拉伸实验数据的进行拟合，采用了Polynom ial，N=1(Mooney-Rivlin)、Polynomial，N=2、Neo hooke、Arruda-Boyce、Vander Waals五种模型。对于没有给出的其他硬度的拟合曲线，其拟合结果的规律一致，由拟合的结果可以看出，除了Polynom ial模型拟合的曲线和实验曲线差距比较大，其它的模型都能比较好的模拟材料的力学性能，其中最接近实验曲线的模型是Neo hooke模型，采用SI单位量纲系统，拟合的参数结果见表1。

图1 橡胶材料拉伸试验

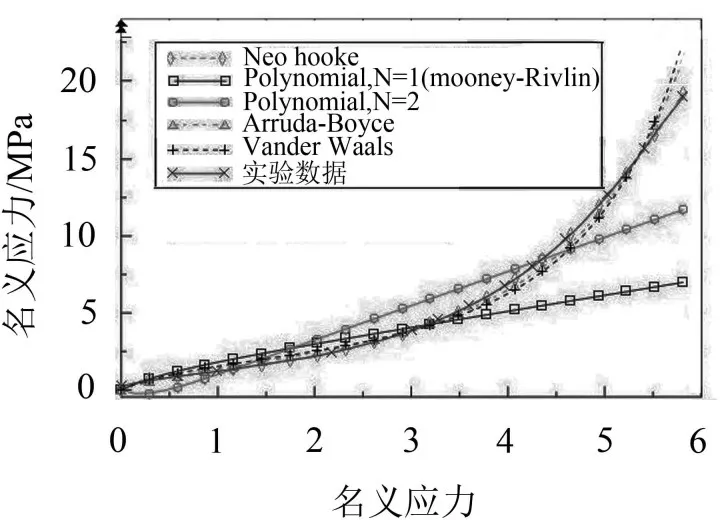
图2 运用不同本构模型拟合的应力—应变曲线

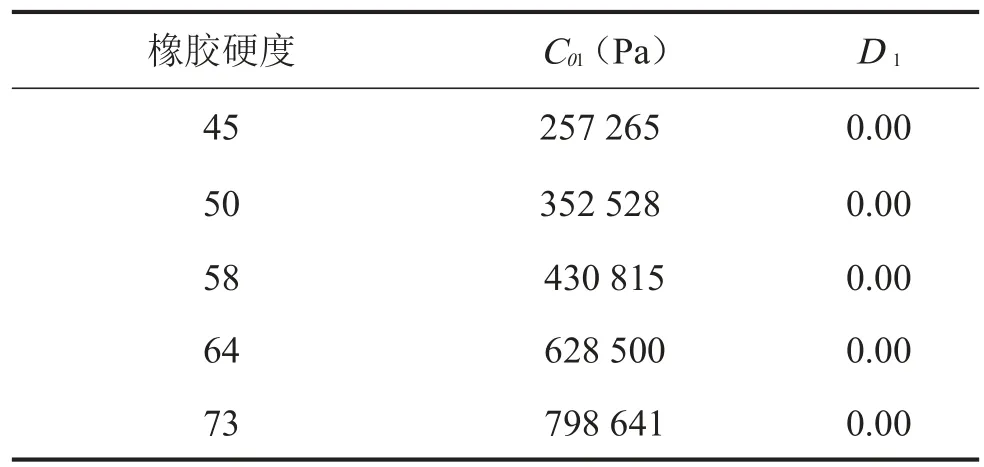
表1 不同硬度橡胶Neo hooke模型拟合参数结果

2 风力发电机弹性支承使用工况

目前2 MW风力发电机已在市场广泛使用，本文研究的双馈异步发电机组的额定功率为2 080 kW，重量为6.7 t，发电机的转速范围为1 000 r/min～1 930 r/m in，额定转速为1 750 r/m in，发电机额定转矩为12.12 kN·m，发电机弹性支承跨距是1 060 mm，刚度要求为8×(1±15%)kN/mm。

采用单层隔振系统，在机脚处共装有四个弹性支承，对发电机有支承和减振作用。发电机弹性支承有两种工作状态，一是当发电机不发电时，支承只受发电机自身的重力，单个支承承受载荷为16.75 kN；二是当发电机发电时，弹性支承还要承受发电机产生的扭矩，额定扭矩产生的动载荷为5.72 kN，加上承受的重力，单个支承承受载荷为22.47 kN。

3 弹性支承有限元建模分析

弹性支承的上板与风力发电机连接，下板与基座连接，中间为橡胶嵌入三块金属板，分别对其整体和1/4截面进行有限元建模分析，如图3、图4与图5所示。

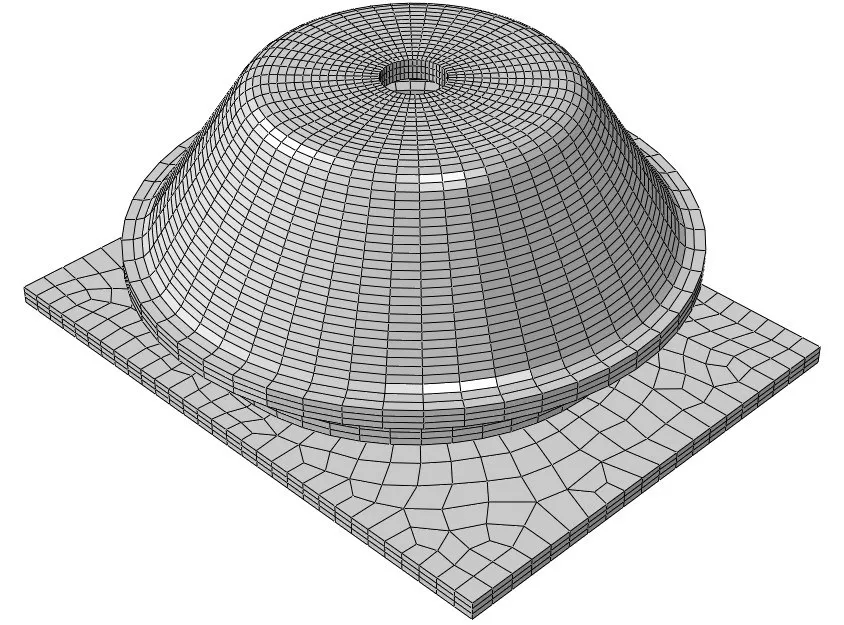
图3 整体模型

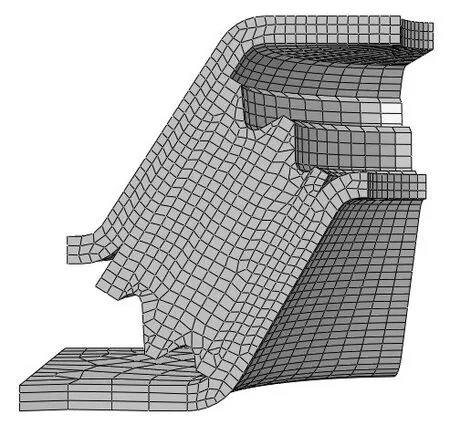
图4 四分之一模型

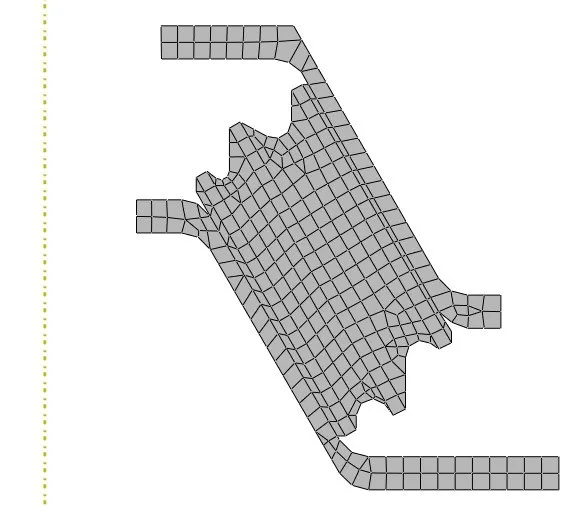
图5 轴对称模型

在模型的构建中，橡胶材料和刚板的粘合面采取共节点的绑定约束，为较好地模拟工程实际；同时采用三维的整体模型1/4模型与二维的轴对称模型。整体模型有26 752个单元，1/4模型有6 411个单元。在三维模型中，采用C3D8RH单元进行仿真计算。由于风力发电机弹性支承主体部分的几何模型、材料模型、边界条件均满足对称要求，采用轴对称模型进行非线性仿真，能够大大节省计算成本。在二维建模中，四结点的四边形单元通常比三结点的三角形要好。轴对称模型采用CAX4R单元能较好的模拟此型号的弹性支承的性能。上述所建模型均合理的避免在分析过程中的体积闭锁和剪切闭锁等现象。

分别计算了三种模型在载荷16.75 kN下的静刚度值，从表2显示的计算结果可知，与三维整体模型相比，二维模型的计算结果有25%～35%的误差；在三维模型中，1/4模型比整体模型大大节省了时间（见表3所示），且计算结果较为接近。综合考虑，下文的计算分析主要采用1/4模型进行。

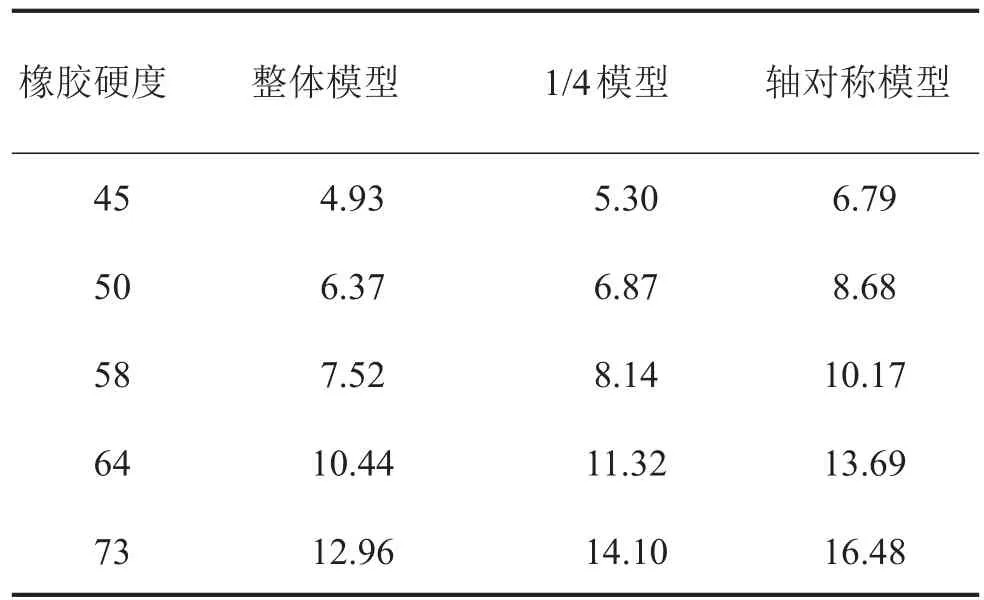
表2 不同模型的静刚度计算结果

表3 不同模型静刚度计算时间

3.1 垂向刚度

垂向刚度是重要的性能指标参数。弹性支承正常工作时，上金属承受来自风力发电机的压力，下板与机舱托架固定。为了模拟真实的受力状态，在上表面施加均布压强，在底面施加固定约束。图6为不同橡胶硬度弹性支承在不同载荷下的位移变形图，其载荷—变形曲线呈现非线性。由结果知，硬度值为58度时，载荷为16.75 kN时，变形为2.05 mm，刚度值为8.14 kN/mm；载荷为22.47 kN时，变形为2.66 mm，刚度值为8.45 kN/mm。

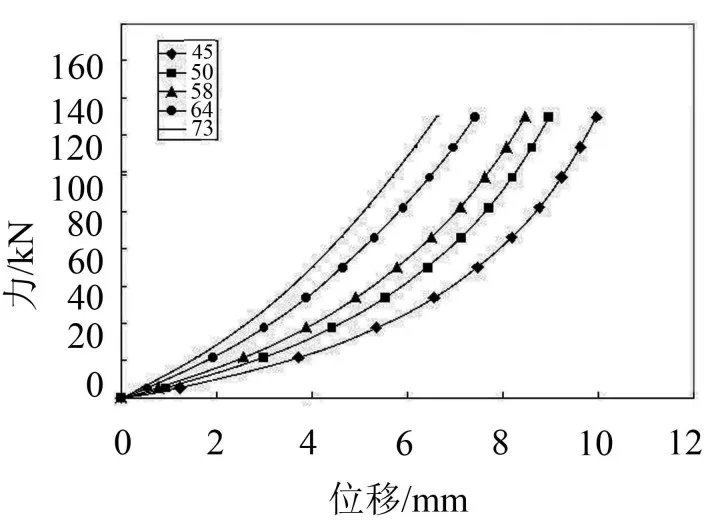
图6 不同橡胶硬度弹性支承的垂向载荷—变形曲线

3.2 横向刚度

弹性支承在受横向载荷的同时必定承受垂向载荷，在软件中首先施加垂向载荷16.75 kN。然后添加横向载荷。对于硬度为58的橡胶材料，得到的横向载荷—变形曲线如图7所示，在载荷为16.75 kN时，横向位移是2.31 mm，刚度值为7.25 kN/mm。

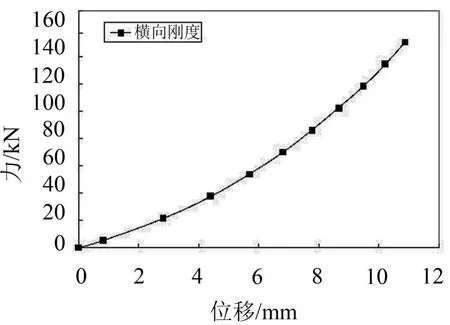
图7 弹性支承的横向载荷—变形曲线

3.3 模态分析

以弹性支承的上板定义质量单元，加载重力载荷，以等效20 kN工作载荷。图8为发电机弹性支承的第1阶振动模态，固有频率为9.68 Hz。发电机的额定转速为1 750 r/m in，扰动力频率为29.16 Hz，故可达到89%的隔振效果。第2阶固有频率为102.18 Hz。

图8 发电机弹性支承的第1阶振动模态

3.4 应力分析

图9为发电机组弹性支承中钢铁件在25 kN载荷下的应力分布图，由结果看出，应力最大值为107.9 MPa，出现在外壳体的内孔边缘，而Q235的屈服强度为235 MPa，故满足使用条件。橡胶件的应力分布见图10，最大应力值为1.33 MPa，出现在钢铁件和橡胶材料的接触部位，没有明显的应力集中现象。橡胶材料受剪切力的许用应力值为2 MPa，承受压缩力时的许用应力值为5 MPa，满足使用要求。

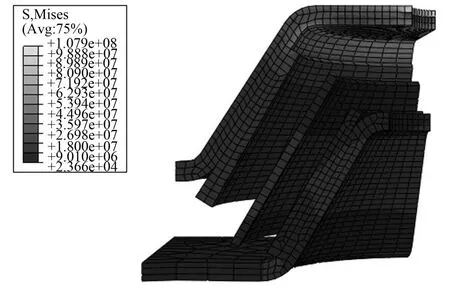
图9 钢铁件的应力分布情况

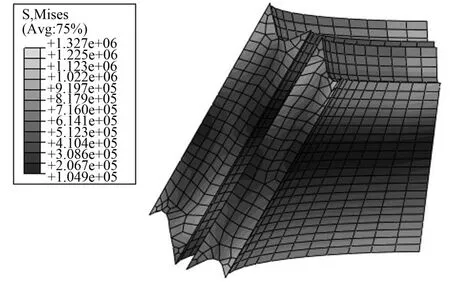
图10 橡胶材料的应力分布情况

4 发电机弹性支承性能试验

风力发电机弹性支承的刚度在微机控制电液伺服橡胶试验机上进行，型号为WXJ-200，最大试验力200 kN。图11为测量垂向刚度试验，测得弹性支承在静载16.75 kN下的刚度值为8.83 kN/mm，有限元计算结果为8.14 kN/mm，误差为8.5%。横向刚度试验相对比较复杂，将弹性支承安装好，在垂向施加20 kN载荷并持载，然后对弹性支承进行横向加载试验，得到横向刚度为7.61 kN/mm，有限元计算结果为7.25 kN/mm，误差为4.9%。仿真结果与实验结果的误差在工程应用允许误差15%范围内，说明本文建立的弹性支撑计算模型是正确的，可为产品的设计开发提供指导。

图11 风力发电机弹性支承垂向刚度试验

5 结语

通过有限元软件对风力发电机弹性支承进行性能分析，并与试验结果对比，可以得到以下结论：

（1）运用有限元软件对橡胶材料应力—应变实验数据进行拟合，Neo Hooke应变能函数模型可以较准确地描述该类橡胶材料的力学性能；

（2）本文建立的弹性支撑整体模型、四分之一模型和轴对称模型中，四分之一模型的计算结果误差较小，并能大大节省计算时间；轴对称模型由于模型简化程度最高，计算结果有较大误差，但计算速度最快；

（3）非线性有限元方法，可用于风力发电机弹性支承的性能研究，为大功率风力发电机弹性支承的设计开发提供借鉴。

[1]胡伟辉，林 胜，李 晓，张亚新.1.5 MW风力发电机组发电机减振器的研制[J].产品开发与设计，2009，36 (1)：64-66.

[2]陈 莲，周海亭.计算橡胶隔振器静态特性的数值分析方法[J].振动与冲击，2005，24(3)：120-123.

[3]刘柏峰，朱海潮，束立红，王宇飞.聚氨酯隔振器特性的有限元分析[J].噪声与振动控制，2011，4(1)：131-135.

[4]黄友剑.城市地铁轨道减振器结构及性能研究[D].长沙：中南大学，2004：29-30.

[5]卜继玲，黄友剑.轨道车辆橡胶弹性元件设计计算方法[M].北京：中国铁道出版社，2010.

[6]Boyce M C,Arruda E M.Constitutive models of rubber elasticity[J].Rubber Chem istry and Technology,2000,73 (3):504-552.

Finite ElementAnalysis of Elastic Support Performance of Wind Turbines

CHENG Rong1,WEN Hua-bing1,LIU Chun-qi2, LV Yu2,SHEN Chao-m ing1

（1.Institute of Vibration and Noise,Jiangsu University of Science and Technology, Zhenjiang 212003,Jiangsu China; 2.Zhenjiang Tieke Rubber Products Co.Ltd.,Zhenjiang 212021,Jiangsu China）

The nonlinear mechanical property of rubbers can directly affect the vibration reduction performance of elastic supports of w ind turbines.In this paper,the experimental data of rubber tension and compression tests is fitted by finite element analysis software,and an optimal rubber constitutive model is derived.According to the working condition of the elastic support,reasonable working parameters and material parameters of the rubbers are selected to establish the global model,a quarter of the model and the axisymmetric model for the elastic support of the w ind turbines.Then,the three models are calculated and the results are compared carefully.The quarter of the model is selected to analyze the performances of the elastic support,such as the nonlinear vertical stiffness,lateral stiffness and natural frequencies and so on.The experimental results show that the finite element analysis is effective.The work is of significance for design of new elastic supports of w ind turbines.

vibration and wave;vibration isolation;w ind turbine;elastic support;nonlinear;finite element analysis

1006-1355(2014)04-0209-05

TB53；U661.44 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.046

随之目前风力发电机功率的不断增大，对机组的振动、噪声、安全稳定性能等方面也带来众多的不利因素。目前采取的措施主要是在减振设计中风力发电机和基座之间安装一组按特定方式排列、具有一定刚度和阻尼匹配特性的减振组件进行减振设计。

2013-09-17

江苏省工业支撑项目（项目编号：BE2011154）

程 荣（1989-），女，江苏常州人，硕士研究生，目前从事噪声振动控制研究。

E-mail:chengrong_071@126.com

温华兵(1977-)，男，江西吉水人，副教授，目前从事噪声振动控制研究。

E-mail:wen-huabing@163.com