振动噪声信号分离优化算法研究

焦金平，刘 冬，刘国艳

（1.上海开放大学 闵行二分校，上海200040；2.上海交通大学 科学技术发展研究院，上海200240）

振动噪声信号分离优化算法研究

焦金平1，刘 冬2，刘国艳1

（1.上海开放大学 闵行二分校，上海200040；2.上海交通大学 科学技术发展研究院，上海200240）

机械振动信号中混杂的背景噪声对信号的分析处理以及振动结构的建模有很大影响，在独立分量分析（ICA）理论研究的基础上，以信息论中的最小化互信息准则作为ICA的判据，提出了一种基于负熵的FastICA共轭梯度快速算法。该算法计算效率高，收敛性能好；适合对初始点不敏感和对鲁棒性有要求的信号处理。实验结果表明了对振动信号的背景噪声分离具有较好的效果。

振动与波；独立分量分析；噪声；信号处理；共轭梯度法

独立分量分析是在传输信道未知的情况下，从一个传感器阵列的输出信号中顺序分离或估计原信号的波形。其基本模型可描述为[3]

式中A为N×N的混合矩阵；x为V×1维观测信号矢量；s为N个统计独立的源信号组成的列向量。ICA的目的就是寻求一线性变换W(即分离矩阵)，通过它能由观测信号恢复源信号。Fast ICA是ICA的一种快速算法，为降低计算复杂度和对信号去相关，先对观测信号x作白化处理，使其变为均值为0、协方差矩阵为单位阵的信号。

因此，关键问题是求分离矩阵W，以便仅通过观测信号x分离出源信号s，数学模型为

其中y为对源信号s的估计。针对振动噪声信号利于批处理的特点，建立最优化目标函数与其算法求解，使输出y尽可能非高斯化，则y的非高斯性的每一个局部极大值给出一个独立分量。

本文以信息论中的最小化互信息准则作为ICA的判据，互信息是衡量随机变量间独立性的尺度，用负熵来表示互信息为

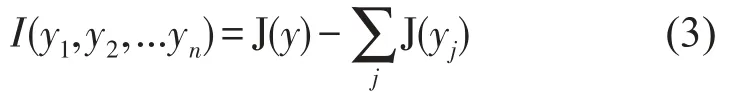
其中J(y)表示y的负熵。当信号y中的各分量相互独立时，最小化互信息就等价于最大化各分离成分的负熵之和。负熵可以由下式近似

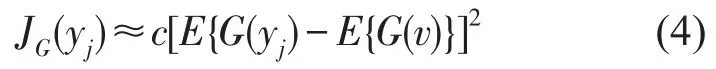
其中c是常数，v是具有零均值、单位方差的高斯变量，yj是零均值、单位方差的变量，E表示期望运算，G(.)是非线性、非二次的函数[4]，经验中常取G(y)=-exp(-y2/2)，此时，就需要问题转化为找出权值矩阵W，使分离出的估计信号y=WTx能使函数JG(yj)最大。

2 共轭梯度算法

共轭梯度法对最速下降法收敛特性进行改进。可以证明：任何一般函数可以在最优点附近用一个二次函数取得较满意的近似，任何使用共轭方向的极小化方法都会二次收敛。因此，使用共轭梯度法可在n次内迭代收敛。其核心为求正交基的思想，它采用所有前面的搜索方向和最后一次梯度的线性组合作为下一个新的搜索方向，因此收敛速度很快[5—7]。

2.1 算法原理

定义目标函数为

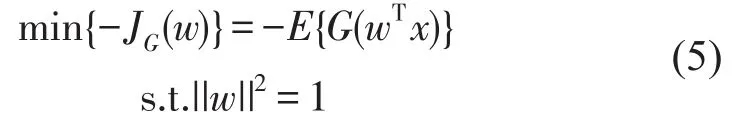
其中w为矩阵W的列向量。前面提到负熵由式(4)近似的条件是yj是零均值，单位方差的变量。对于已白化的观察信号x，这就等价于限制w的范数为1。转化成无限制条件的优化问题，得到惩罚函数

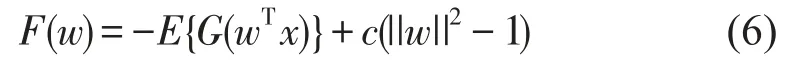
F(w)的梯度为

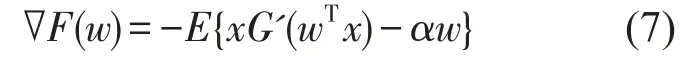
其中α为常数，G’为G的导数。

w的计算步骤如下

(1)设定初始点w1，允许误差 ε＞0，置d1=-∇F(w1)；

(2)若|∇F(wk)|≤w，则 停 止 计 算 ，否 则wk+1=wk+λkdk；

(3)归一化处理为wk+1=wk/||wk+1||，其中步长λk为{1，α1，α2，α3，...}，（0＜α＜1）则 满 足F(wk+λkdk)=mλin F(wk+λdk)；

(4)令dk+1=-∇F(wk+1)+βkdk

(5)置k=k+1，转步骤(2)。

2.

2算法分析

如果算法中每一步迭代的步长λk均采用精确一维搜索，必有但精确一维搜索单次耗时太长。我们通过适当的选择对比函数G (u)来实现全局收敛的目标。可以证明，如果目标函数满足假设(H)

（1）f(x)在水平集L1={x∈Rn|f(x)≤f(x1)}上有下界；

（2）f(x)在水平集L1的某邻域D内连续可微，且其梯度函数g(x)是Lipschitz连续的，即存在一个常数L＞0，使得|g(x)-g(y)||≤L||x-y||,x,y∈D。

且算法步骤3中对步长λk的选择，即式(9)作适当修改，则共轭梯度算法产生的序列具有全局收敛性。实验中，取G(u)=1/4u4，由此产生的目标函数F (w)满足假设（H），且由于该G(u)是凸函数，共轭下降算法对凸函数具有二次收敛性，故满足假设（H）的凸函数是计算快，稳定性好的对比函数。

除迭代次数远少于梯度下降法外，该算法对初始点无要求。而牛顿法对初始点要求较高。当所选的初始点远离极小点时，牛顿法可能不收敛，因为牛顿方向不一定是下降方向。且牛顿算法需要求Hessian矩阵逆的复杂运算，而该算法只涉及到求一阶导数，复杂度较低。

该算法存储量小。一个样本只需存储3个n维向量。因此，对于样本数多的大规模问题，采用该算法可显示出优点。

3 实验分析

实验的最终目的在于研究电机外壳振动与辐射噪声的相干性，加速度传感器和电容式麦克风分别用于采集加速度信号和辐射噪声信号。通过麦克风采集的声场数据含有大量环境噪声信号，严重影响了微弱信号处理的效果，所以必须通过一定的方法把背景噪声从信号中分离。考虑采用ICA的方法，声场麦克风布置示意图如下：

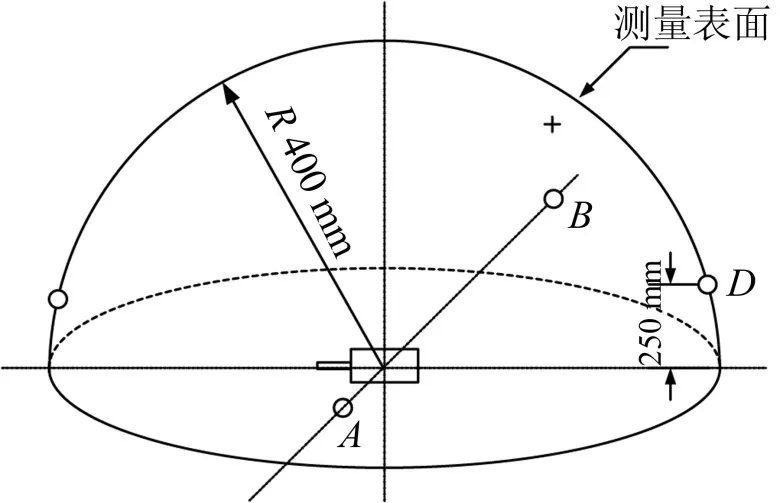
图1 麦克风布置

根据GB/T 10 069.1—2006中附录C的要求，噪声测试时的测试面为半球形，测试半径为0.4 m，测点高度为0.25 m。在图示A、B和C、D两组测点分别布置麦克风进行两次测试，进一步消除传感器位置的影响。

经过平均处理后，两个传感器得到的混合噪声信号见图2。

图3为经过基于共轭梯度法的Fast ICA方法分离得到的电机振动辐射噪声和背景噪声。对比传感器信号，背景噪声对辐射噪声的测定影响很大，而该算法方法结果较为理想。分离结果是在允许误差ε取0.000 1时，在普通配置的PC机上运行80 s得到。该算法运行时间不随采样点的增多显著增长，这进一步验证了算法的计算复杂度低，收敛快的特点。若ε取更小值，分离精度提高不多，但却消耗大量计算时间。G(.)选取不同的函数对分离效果和收敛速度的影响与算法分析相一致。此外同一G(.)对服从不同概率分布的信号源分离的效果不同。选择比G(u)=1/4 u4增长得慢的函数，如对数函数，算法的鲁棒性更好。

将分离后的两种信号量值平均后用三分之一倍频程形式表示如图4，注意到，低于125 Hz的频率范围内，背景噪声的声压级反而大于电机运行噪声的声压级，连续三次的测量结果表明，在这个频段内（20 Hz～125 Hz），背景噪声与电机运行噪声的关系很不稳定，前者时而大于后者、时而小于后者。出现这种情况可能有两个原因：

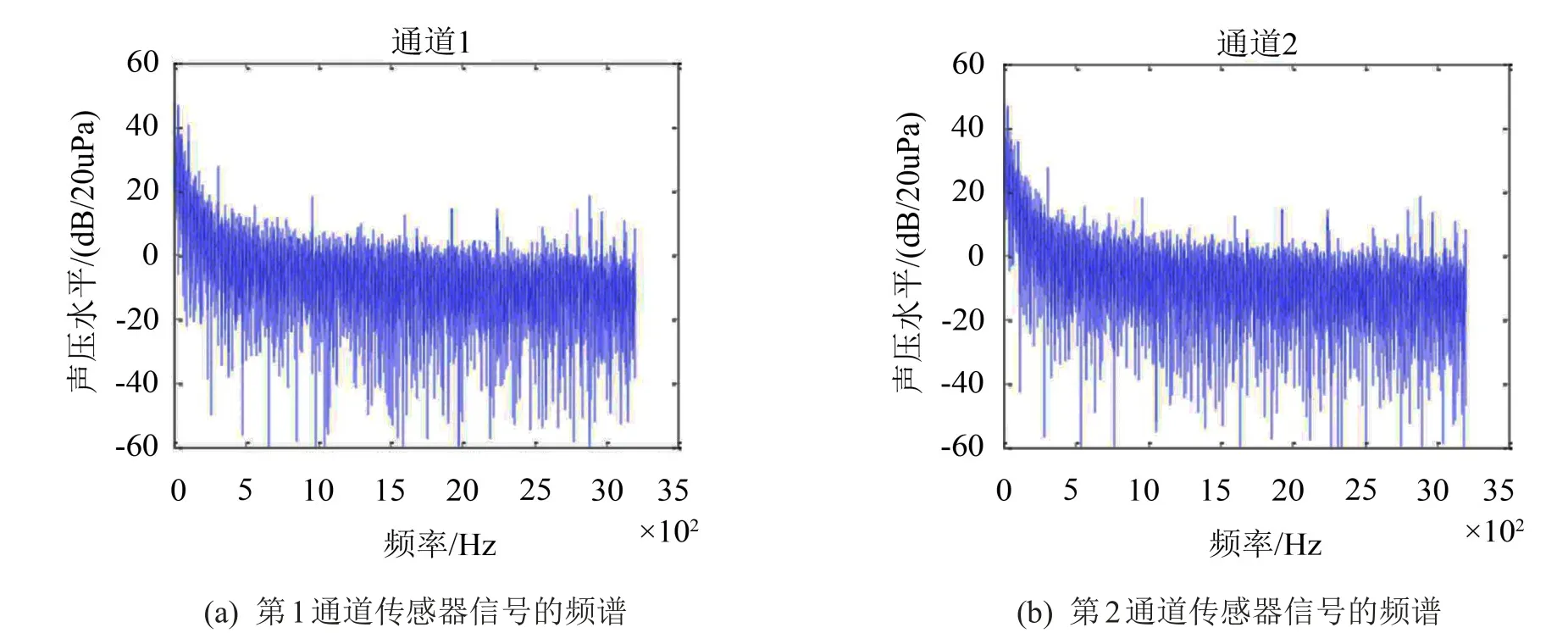
图2 加速度传感器采集信号

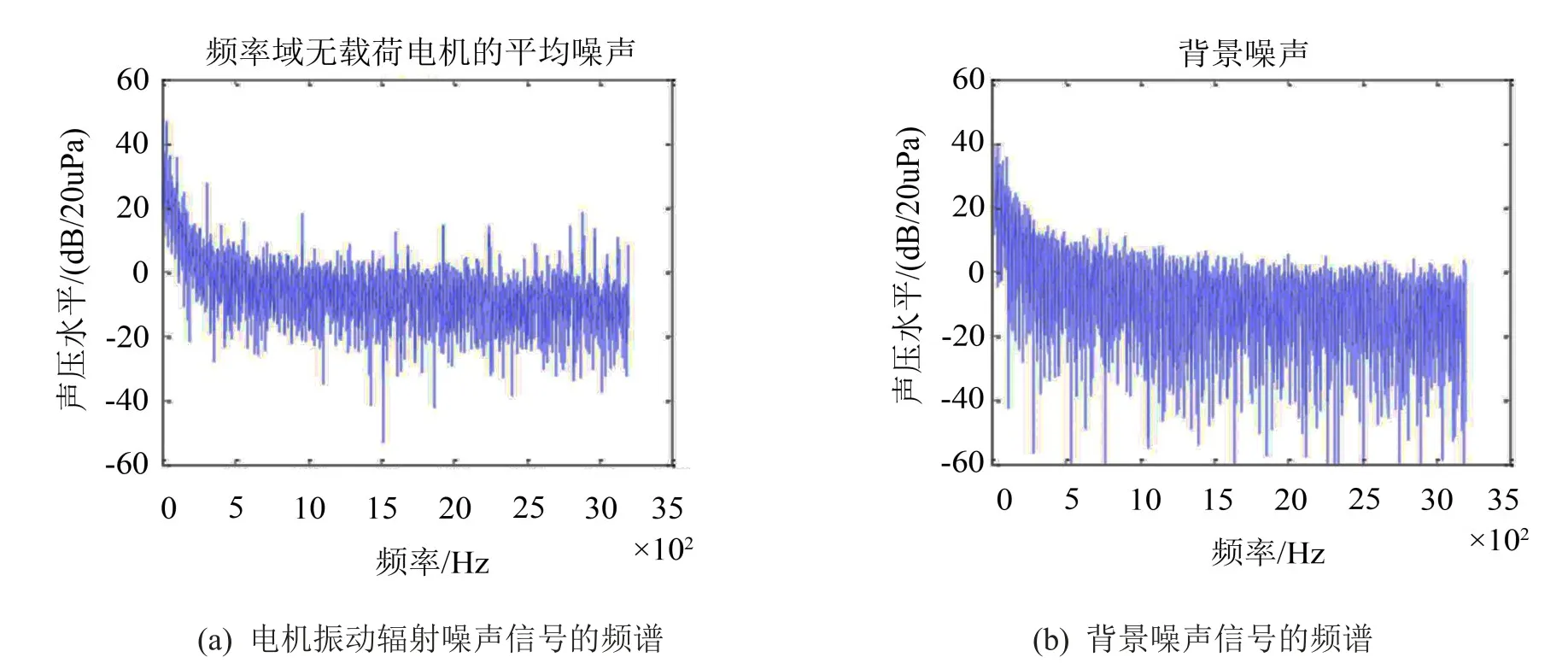
图3 分离后的两种噪声信号

(1)：没有使用消声室，低频段干扰源多，背景噪声声压波动大；

(2)：声场麦克风在20 Hz～125 Hz范围内的灵敏度较差，结果不可信。

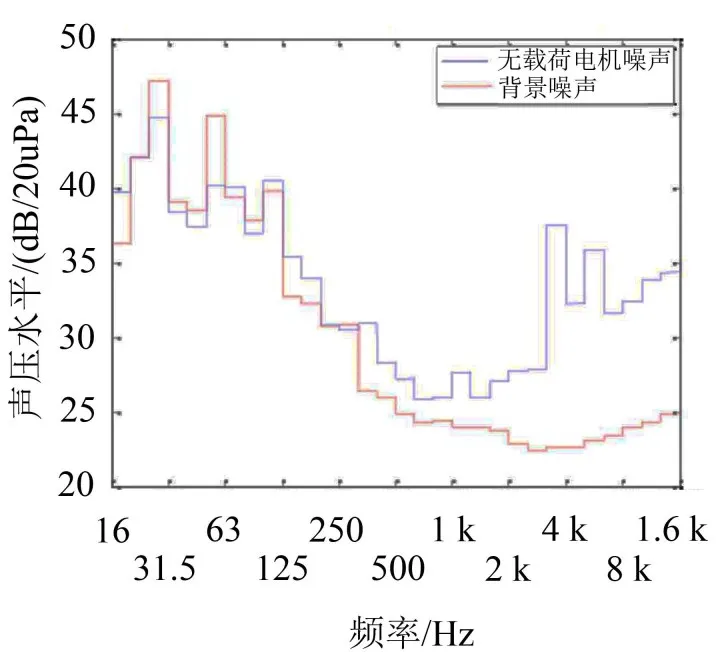
图4 背景噪声和电机运行噪声的1/3倍频程表示

4 结语

本文提出了一种基于熵的Fast ICA的共轭梯度算法。实验证明了独立分量分解在信号分离中的有效性，该算法在收敛速度和对初始点的敏感性之间取得了平衡，而且在适当的条件下具有全局收敛性。该算法仍存在需改进之处，如：缩短线搜索的时间能进一步提高算法的收敛速度；选择合适的对比函数使算法既能适用于不同概率分布的信源，又具有较低的计算复杂度。

[1]范 涛，李志农，卢纪富，员险锋.基于变分贝叶斯独立分量分析的故障源盲分离[J].噪声与振动控制，2012，(1)：82-85.

[2]朱 虹，蔡 丹，吕震中.采用Fast ICA的压力信号消噪[J].噪声与振动控制，2009，(6)：140-142.

[3]A.Hyvarinen,et al.Independent Component Analysis[M].John Wiley and Sons,2001.

[4]A.Hyvarinen.Fast and robust fixed-point algorithm for independent component analysis[J].IEEE Trans.Neural Network,10(3),626-634,1999.

[5]HAN Ji-ye,LIU Guang-hui,YIN Hong-xia.Convergence properties of conjugate gradient methods w ith strong wolfe line search[J].Syst SciMath Sci,2000,11(2):112-116.

[6]Z.Fu and E.M.Dow ling,Conjugate gradient eigenstructure tracking for adaptive spectral estimation[J].IEEE Trans.Signal Processing,1995,Vol.43,512-516.

[7]Amari.S.L.Cichocki.A.＆Yang.H.A new learning algorithm for blind source separation advances in neural [J].Information Processing Systems,1996,Vol.8:757-763.

Research of OptimalA lgorithm for Noise Signal Separation

JIAO Jin-ping1,LIU Dong2,LIU Guo-yan1

(1.Shanghai Open University,M inhang Second District,Shanghai 200240,China;
(2.Office of Research Management,Shanghai Jiaotong University,Shanghai 200240,China)

Background noise in the mechanical vibration signals has a great influence on signal processing and structural modeling.In this paper,a FastICA conjugate gradient algorithm based on negative entropy and independent component analysis(ICA)is presented.This algorithm has advantages of high computation effect,good convergence performance and robust.The experimental analysis results demonstrate the effectiveness of the proposed method in vibration signal separation from the background noise.

vibration and wave;independent component analysis;noise;signal processing;conjugate gradient algorithm

1006-1355(2014)04-0157-04

TB53；TP202+.7 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.034

电机在空载和稳态运行情况下的机壳振动与辐射噪声互有紧密的关联，通过加速度与声压级的对比分布和具体测试，可以分析机壳表面振动对辐射噪声的影响。但是，测试所采集的信号却不可避免地包含了各种背景噪声；如传感器受到各种环境的随机激励，以及信号中混入了除振动信息外的其他随机成分等等。为了保证所测试振动信号的真实和可靠，并随后进行分析与识别，降低背景噪声就显然十分重要。若噪声源的功率谱很接近，使用传统的频域分析方法很难准确获取特定的信号，因此，研究干扰环境下的噪声源信号分离的方法，具有很重要的意义。

独立分量分析（ICA）是一种典型的盲信号分离（BSS）方法，通过假定各源信号相互统计独立，可以从混合信号样本出发，分离出各个源信号的估计。利用该技术可把各种混叠的噪声分离成为互不相关的独立信号，从而为某个特征的提取提供了保证[1，2]。

1 Fast ICA的基本概念、原理和算法

2013-09-22

焦金平（1974-），男，山西芮城人，硕士研究生，讲师，研究方向：计算机应用。

E-mail:jiaojp@163.com