考虑设备弹性的隔振系统

高 阳，孙玲玲，王晓乐

（山东大学 机械工程学院，济南250061）

考虑设备弹性的隔振系统

高 阳，孙玲玲，王晓乐

（山东大学 机械工程学院，济南250061）

针对被隔振设备在高频域表现出的弹性阻抗特性，将设备中具有弹性性质的支撑部分模化为两端自由连续体，确定振源输出作为一个常力作用在设备支撑上，同时考虑设备支撑的刚体运动与弹性振动。采用导纳矩阵法对设备支撑的阻抗特性及隔振系统的功率流传递特性进行研究。结果表明，振源激励力在设备支撑上的位置对系统隔振效果具有较大影响。当激励力偏心时不仅引起系统横摇振动，还会激发设备支撑与基础的偶数阶模态，导致隔振效果变差。隔振器相对设备支撑中心或基础中心不对称布置会激发基础偶数阶模态，且前者还会导致垂向—横摇耦合振动。分析的结果对于弹性基础隔振效果的改善有参考价值。

振动与波；隔振；弹性设备；导纳；功率流

将被隔振设备分为刚性机器与弹性设备支撑两部分，本文主要对后者弹性特性进行研究，因此忽略刚性机器的影响，将其视为振源且输出一常力作用在设备支撑上，以导纳法着重探讨了振源激励点位置与隔振器安装位置对设备支撑刚体模态与弹性模态的影响，以期为工程隔振评估提供理论依据。

1 系统力学模型

将被研究系统分为设备支撑A、隔振器B和基础C三个耦合子系统。将设备支撑结构考虑成两端自由梁，基础考虑成两端固定梁。设备支撑与基础通过隔振器连接，为分析方便，暂且将隔振器考虑成集中参数系统。整个系统如图1所示，其中F，V分别为振源输入设备支撑的力与速度。系统动力传递关系如图2所示。

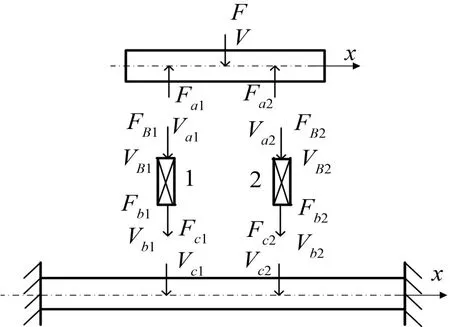
图1 系统模型

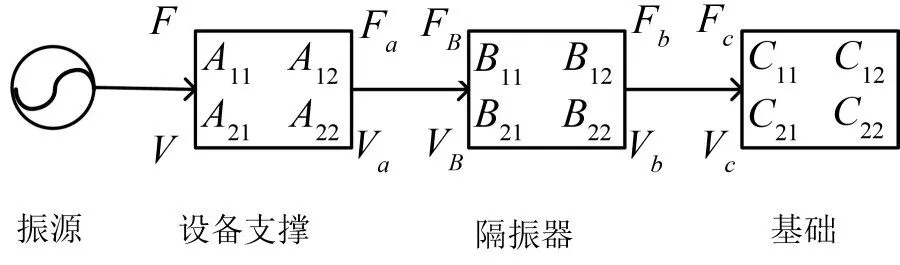
图2 系统动力传递

1.1 设备支撑子系统A

对于两端自由梁，同时考虑其弹性模态与刚体模态，推导其导纳矩阵

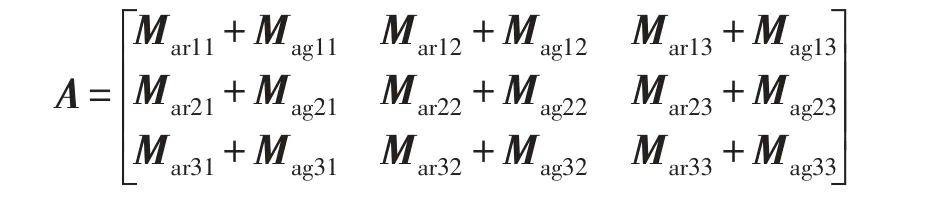
其中MarijMagij分别为弹性导纳与刚体导纳；则子系统A动态特性有如下关系

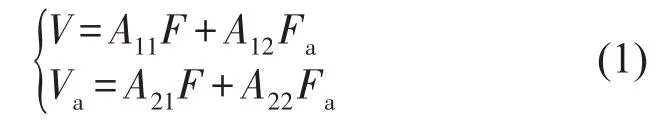
其中

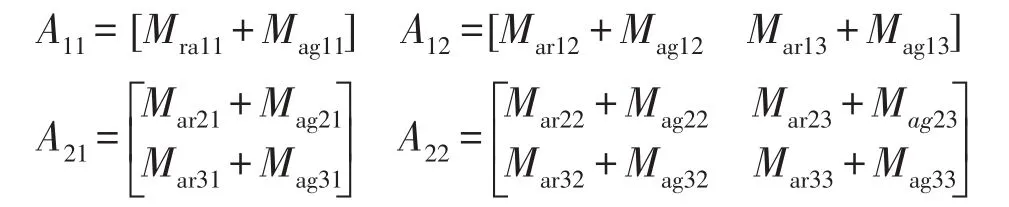
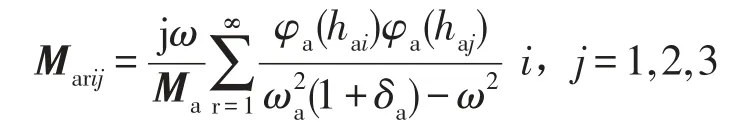
其弹性导纳为为设备支撑固有频率；

ha1,ha2,h3a分别为激励点与隔振器1，2坐标位置；

φa为振型函，根据文献[13]有

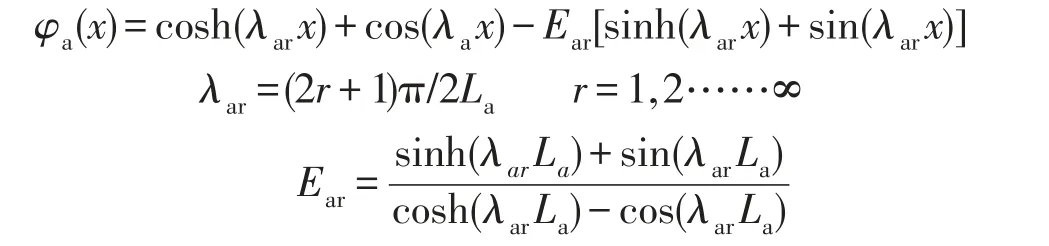
由刚体运动理论得

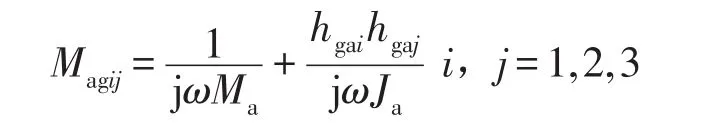
其中La，Ba，Ha，ρa，Aa，Ia，Ma，δa，Ja，Ea分别为设备支撑的长，宽，高，密度，横截面积，截面惯性矩，质量，阻尼因子，转动惯量与弹性模量。

1.2 隔振器子系统B

隔振器考虑成集中参数系统，根据四端参数法，有

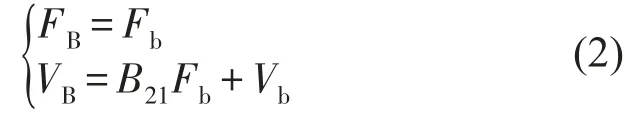
其中FB=[FB1FB2]T,VB=[VB1VB2]T分别为输入到隔振器的力与速度；Fb=[Fb1Fb2]T，Vb=[Vb1Vb2]T分别为隔振器输出的力与速度。且有

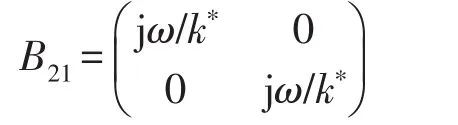
k∗=k(1+jδb)为复刚度，k，δb分别为隔振器动刚度与阻尼因子。

1.3 基础子系统C

基础系统C满足

其中FC=[FC1FC2]T，VC=[VC1VC2]T分别为输入到基础的力与速度。矩阵C为基础导纳矩阵，且

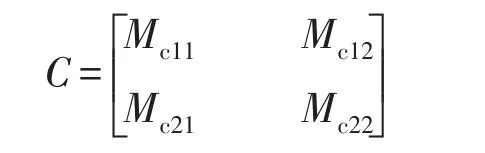
将基础考虑成两端固定梁，隔振器1，2在基础上的坐标分别为hc1hc2，其导纳为

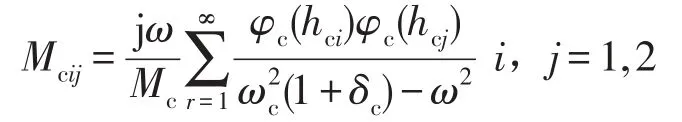
式中振型函数与固有频率表达式参考文献[13]。导纳中各项参数含义与设备子系统中相同。

1.4 系统功率流

根据(1)(2)(3)式即可得

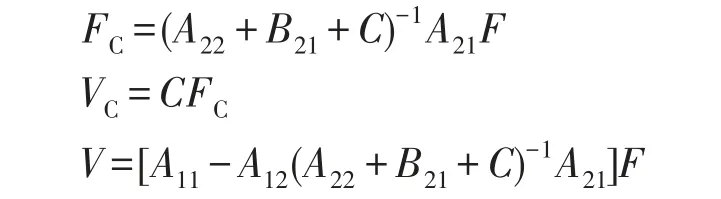
则输入基础的功率流Pc为

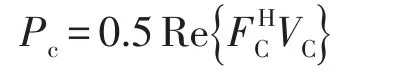
其中H表示对矩阵取共轭转置运算。

2 系统参数

对外界激励点位置ha1，隔振器1、2在设备上的安装位置ha2、ha3以及隔振器在基础上的安装位置hc1、hc1参数由如下关系确定

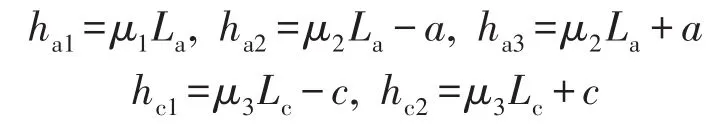
其中μ1=μ2=μ3=0.5，a=c=0.4 m。

系统的结构参数与各阶固有频率分别如表1，2所示。在此参数下，系统整体垂向振动固有频率理论值为

3 仿真结果与分析

图4给出了将设备支撑考虑成弹性体与刚性体时输入基础的功率流对比。仿真可得系统整体垂向振动模态出现在约6.56 Hz，基础的第1阶模态出现在约70.77 Hz，而在高频段，设备的第1阶模态(158.9 Hz)会被激发，此时设备不能再视为刚体，其整体的弹性振动不能被忽略。

从图4中可以看出，在中低频段内，弹性设备支撑模型与刚性设备支撑模型的功率流谱几乎重合，因此采用刚性模型对于中低频激励具有足够的精度。但是随着激振频率增大，当频率大于80 Hz时，两者差别逐渐变大：高频激励下弹性模型中出现新的共振峰，在其影响下，峰值附近的功率流显著增大，导致这一频段附近的隔振效果明显下降，此时设备支撑不能再考虑为绝对的刚体。对比表2固有频率与图4共振峰位置可以发现，设备支撑与基础仅奇数阶模态被激发，这与振源激励点位置以及隔振器在系统中的安装位置有关。

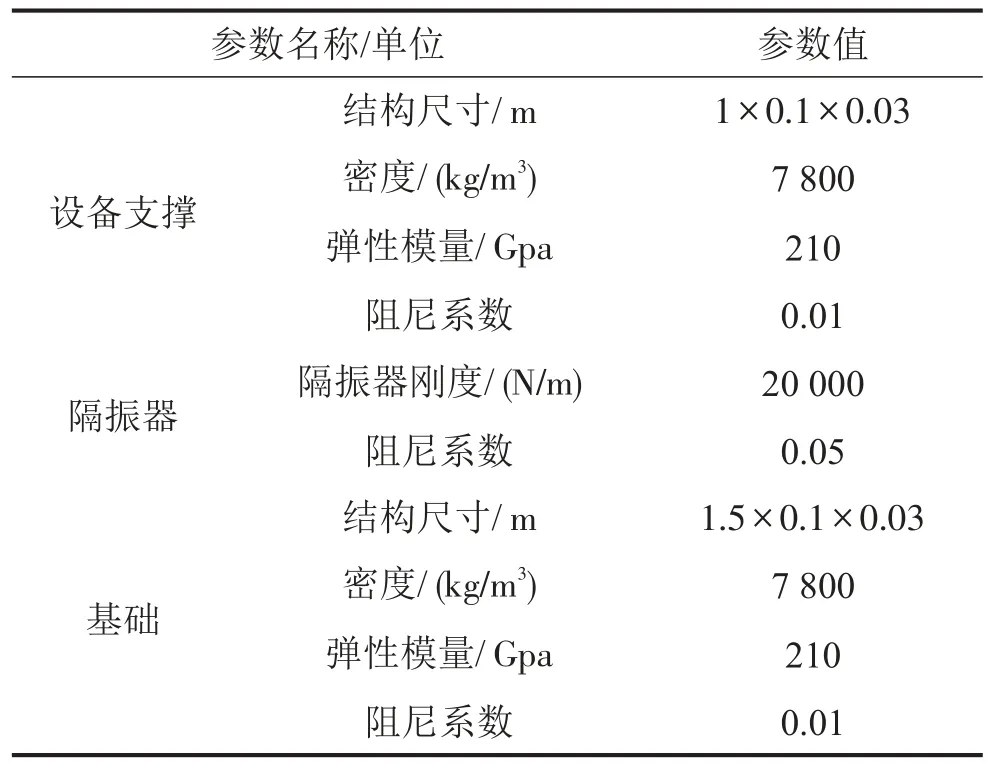
表1 结构参数

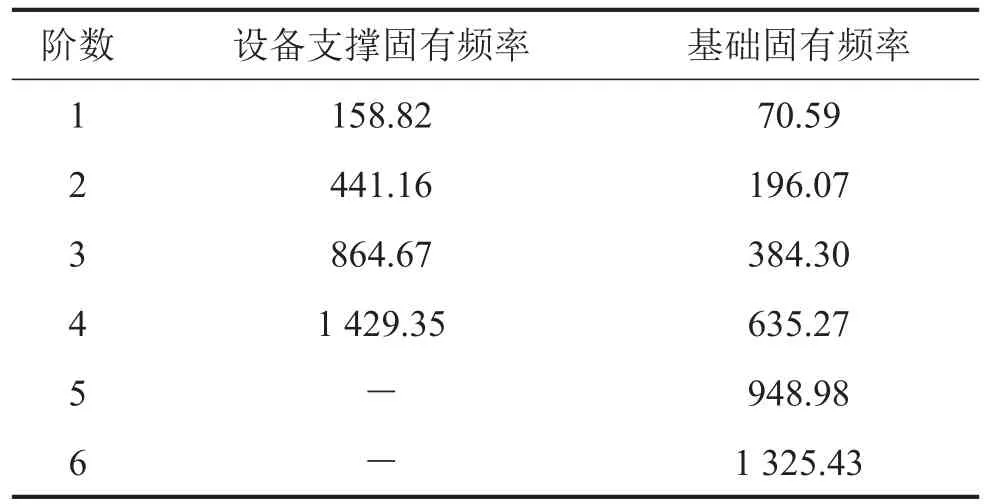
表2 设备支撑与基础横向振动固有频率

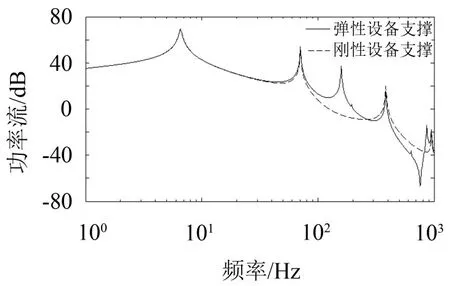
图3 弹性设备支撑与刚性设备支撑的功率流谱

3.1 激励点位置对功率流谱的影响

在本文模型中，认为设备支撑结构为一均质梁，其重心与中心重合。隔振器相对于设备支撑与基础对称安装。μ1=0.5表示振源激励点在设备支撑重心位置。从图5中及表2可以看出，此时只有设备支撑与基础的奇数阶模态被激发。μ1=0.2，振源激励点与设备支撑结构重心不再重合，功率流谱在整个频段均出现了明显差异：在低频率段，系统整体垂向振动模态附近出现1阶共振峰(若距离垂向模态过近则两者重合在一起，使前者峰值变大)，它是由于振源激励点位置与重心位置不重合而引起的系统整体横摇模态，在本文中其理论计算值为导致低频段隔振效果变差；在高频段，设备支撑与基础的偶数阶模态都会被激发，峰值密集，传递到基础的功率流显著提高，隔振效果严重变差；

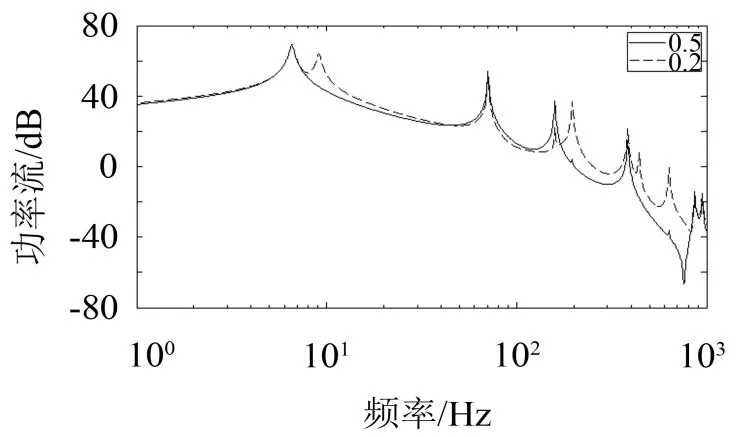
图4 不同振源激励点位置对功率流谱的影响

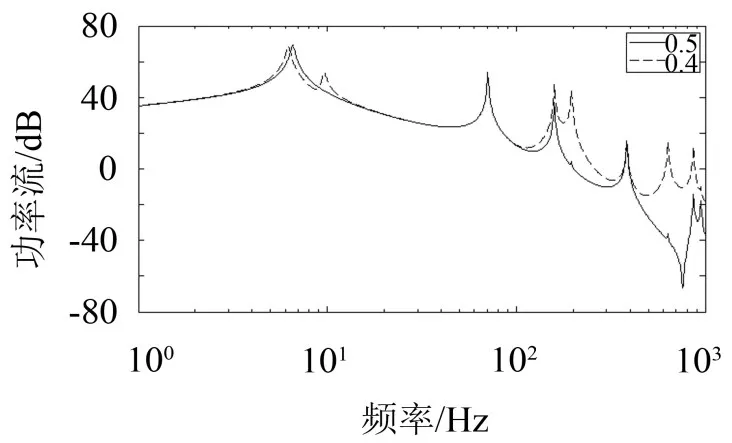
图5 隔振器在设备支撑上不对称时的影响

3.2 隔振器位置对功率流谱的影响

μ2为隔振器在设备支撑上的安装位置参数，μ2=0.5表示隔振器相对设备对称安装。从图6可以看出，μ2=0.45改变后，低、高频段也出现了新的共振峰，但却与图5情况有所不同。在低频段，图5中的偏心激励力可以等效为一作用在重心的垂向扰动力与一扰动力矩，系统整体垂向振动与横摇振动分别由相应的扰动力和扰动力矩引起；图6尽管激振力作用在设备支撑重心，但由于隔振器的布置相对设备支撑不对称，当设备支撑在垂向移动一定距离后，两隔振器的反作用力是相同的，但他们对设备支撑重心的反作用力矩却不相等，因此引起了横摇振动。所以两者振动模式不同：前者可视为两个单自由度来处理，两种振动模式互不影响；而后者为垂向—横摇耦合振动，两者相互影响。由此，图5中μ1变化仅改变等效扰动力矩的大小，对等效垂向扰动力没有任何影响，所以横摇振动模态改变，垂向振动模态重合。图6属于垂向—横摇耦合振动，μ2的改变使横摇振动变化，继而影响垂向振动，所以垂向振动模态不重合。在高频段，基础的全部模态被激发，虽然隔振器在设备支撑上并未对称安装，但是设备支撑仍然只有奇数阶模态被激发。

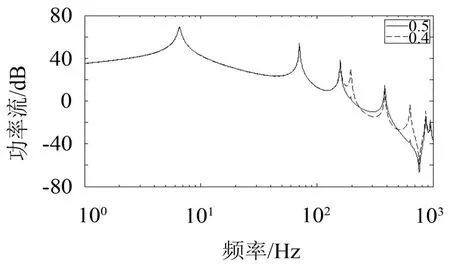
图6 隔振器在基础上不对称时的影响

μ3为隔振器在基础上的安装位置参数，μ3=0.5表示隔振器相对基础对称安装。从图7可以看出，隔振器在基础上不对称时(μ3=0.4)中低频段的差别并不明显，但高频段基础的全部模态被激发，导致功率流谱中振峰密集，隔振效果变差。所以对于工作频率小于基础基频的隔振系统，可以根据工作环境的限制选择在基础上非对称安装。但对于高频激励，应尽量让隔振器在基础上对称布置。此外，不论隔振器在基础上的安装位置如何改变，设备支撑都只有奇数阶模态激发。

4 结语

本文在考虑设备弹性基础上建立了垂向激励的力学模型，探讨了不同振源激励点位置以及隔振器安装位置对功率流谱的影响，通过分析得出：

(1)设备中作为振源的机器部分尽量布置在设备支撑的重心与中心位置。让振源激励点作用在设备支撑的重心与中心可避免低频段系统整体横摇模态以及中高频段设备支撑和基础的偶数阶模态出现，避免峰值密集而导致隔振效果变差；

(2)隔振器在设备支撑与基础上的安装位置尽量对称布置。当隔振器在设备支撑或基础上不对称时都会激发基础全部弹性模态，前者还会引起系统整体垂向—横摇耦合振动，这都使共振峰增多导致隔振效果变差。但是，设备支撑的偶数阶模态对μ2与μ3并不敏感，隔振器安装位置改变不会激发其偶数阶模态。

另外，在考虑设备支撑弹性后功率流谱中可能现向下尖峰模态。研究发现这种模态主要由设备支撑的弹性振动引起，其出现频率取决于设备的物理参数与其上激励点位置，与基础特性无关。

[1]熊冶平，宋孔杰，韩玉长.复杂柔性耦合系统的功率流传递谱[J].声学学报，1996，21(4)：368-374.

[2]Dino Sciulli,Daniel J.Inman.Isolation design for systems w ith flexible base and equipment[J].Proc.SPIE,1998, 3327:378-386.

[3]Gardonio P,Elliott S.J and Pinnington R.J.Active isolation of structure vibration on a multiple-degree-offreedom system,part I:the dynam ics of the system[J].Journal of Sound and Vibration,1997,207(1):61-93.

[4]Gardonio P,Elliott S.J.Passive and active isolation of structural vibration transm ission between two plates connected by a set of mounts[J].Journal of Sound and Vibration,2000,237(3):483-511.

[5]孙玲玲，宋孔杰.复杂机械系统多维耦合振动传递矩阵分析[J].机械工程学报，2005，41(4)：38-43.

[6]Snowdon J C.Vibration isolation:use and characterization [J].Journal of the Acoustical,Society of America,1979,66 (5):1245-1274.

[7]熊冶平，宋孔杰.柔性隔振系统中驻波效应的研究[J].山东工业大学学报，1995，25(2)：108-113.

[8]陈 荣，孙玲玲，吴银兵，等.基于Timoshenko粱理论的斜置隔振系统功率流特性分析[J].振动与冲击，2010，29(9)：97-101.

[9]宋孔杰.考虑振源阻抗影响的动力吸振器[J].固体力学学报，1992，13(2)：141-147.

[10]宋孔杰.高频振动条件下隔振效果的探讨[J].山东工业大学学报，1988，18(4)：79-83.

[11]宋孔杰.设备阻抗和支撑结构阻抗对隔振效果的影响[J].噪声与振动控制，1984，12(6)：2-7.

[12]田国成，宋孔杰，熊冶平.复杂弹性系统的结构噪声控制及最优化设计研究[J].声学学报，1995，20(5)：368-376.

[13]Frank Fahy,Polo Gardonio.Sound and structural vibration[M].Oxford:Academic Press,2007.

Isolation Effect of the System w ith Equipment Support’s Flexibility

GAO Yang,SUN Ling-ling,WANG Xiao-le

(School of Mechanical Engineering,Shandong University,Jinan 250061,China)

The flexibility characteristic of the isolated equipments in high frequency domain is studied.A model,in which the elastic support of the equipment is regarded as a continuum system w ith free ends,is established.The vibration source output is regarded as a constant force applied to the equipment’s support,and its rigid motion and elastic vibration are considered.Then,the characteristics of the flexible equipment’s support and the power flow transmission of the vibration isolation system are studied utilizing admittance matrix method.It is shown that the position of the source excitation has a great influence on the performance of the vibration isolation system.The eccentricity of the excitation force can induce lateral oscillation of the system and inspire even order modes of the support and the base,which w ill lead to poor isolation effect.The non-symmetric distribution of the isolators to the central line of the support or the base can excite the even order modes of the base,and the former can furthermore inspire lateral-pitch coupled oscillation.Results of the analysis may have some reference significance for improvement of vibration isolation of equipments w ith flexible supports.

vibration and wave;vibration isolation;flexible equipment;mobility;power flow

1006-1355(2014)04-0138-04+147+147

TB53 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.030

基础的非刚性，隔振器的分布参数特性以及被隔振设备在高频下刚性不足等性质造成了经典隔振理论与实际隔振效果的差异。为此不少学者使用板或梁等模型来模拟基础结构，讨论其弹性特性对隔振的影响[1—5]；也有学者采用Euler-Bernoulli梁模型[6,7]或Timoshenko梁模型[8]对隔振器进行仿真计算，探讨驻波效应的影响，而对于被隔振设备，仍将其视为绝对的刚体。通常情况下，机器设备本身的刚度非常大，但设备的支撑(如设备的机脚、支撑框架等)在高频下会显得刚性不足,其弹性模态会被激发，使设备显示出弹性体的性质。当激励频率大于设备支撑的一阶固有频率时，就必须考虑其有限阻抗特性。宋孔杰[9—11]对振源阻抗及其输出特性进行了较多的研究，指出只有当振源阻抗为零或者相对基础与隔振器都较小时，才可以将振源输出力视为常值，但对设备的弹性阻抗特性并未涉及；田国成[12]等在前者基础上，将设备考虑成连续弹性体并用子结构阻抗综合法得到了阻抗矩阵,探讨了设备弹性的影响。Sciulli[2]将设备考虑成两端自由Euler-Bernoulli粱，探讨了柔性设备柔性基础单一隔振器不同安装位置和安装频率对传递率的影响；而Gardonio[4]则是将设备考虑成简支板，讨论了多隔振器支撑下输入基础的功率流。上述文献虽对设备弹性进行了探讨，却忽略了设备刚体运动模态，未能将设备刚体运动与弹性振动结合在一起。

2013-10-30

国家自然科学基金资助项目（基金编号：51174126）

高 阳，男，山东济南市人，硕士，目前从事振动与噪声控制研究。

E-mail:gaoyang813@126.com