运行参数与轴流泵流体激励力的关系

张 硕，陈长盛

(1.海军驻704所军事代表室，上海200031；2.中国船舶重工集团 第704研究所，上海200031)

运行参数与轴流泵流体激励力的关系

张 硕1，陈长盛2

(1.海军驻704所军事代表室，上海200031；2.中国船舶重工集团 第704研究所，上海200031)

泵内非定常压力脉动会引发泵体的结构振动，运行工况的变化会改变泵内流场的流动状态，从而对泵的振动特性产生影响。通过流体力学计算软件FLUENT对某台立式轴流泵内流场进行仿真计算，分别改变泵运行速度和流量两项参数，得出转速改变后，叶轮受到的力会偏离了相似理论的计算值；工作在小流量时，泵内压力脉动与叶轮受力均大于大流量工况，且叶轮区域出现流动分离现象，不利于振动噪声的控制。

振动与波；运行工况；轴流泵；压力脉动

计算所用立式轴流泵的设计叶片数为4，可变频调节转速，并可通过阀门调节流量。泵内流场区域的剖面结构示意如图1所示。

将结构模型进行适当简化，并将泵内流场进行分段划分网格，如上图中，将流场分为吸入段、叶轮段、支撑段和接管段以及弯管段等部分。

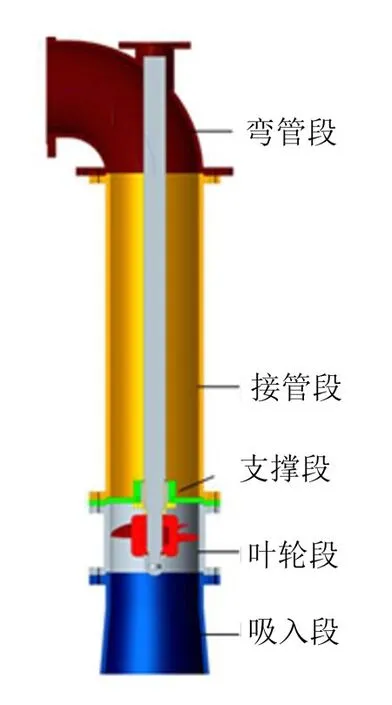
图1 泵内流场区域示意图

由于该泵实际运行环境为开式系统，为保证计算结果精确，在建立流体计算模型时，将水池区域也纳入计算域，且在弯管段后方增加5倍口径长度的出口延伸段，以保证出口流动充分均匀。

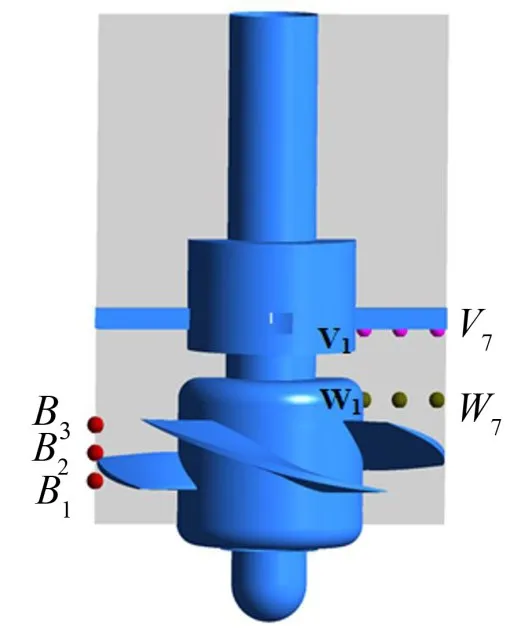
图2 非定常压力监测点(B表示叶轮区，W表示尾迹区，V表示支撑架前缘)

在叶轮区域、尾迹区以及支撑架前缘设置压力脉动监测点。如图2所示。B1、B2和B3监测点在轴的距离为20 mm，B3位于流道尾缘，B2则处于流道中间，B1靠近叶轮流道进口；在叶轮后尾迹区沿径向布置的W1—W7七个测点，它们的相对叶高分别为0%、15%、30%、45%、60%、75%和90%，图中仅标出了W1、W4、W7三个监测点位置；在支撑架前缘按同样方式沿叶高也设了V1—V7七个测点。

计算中，取叶轮旋转1弧度所需时间为T，t/T等于2π正好表示叶轮旋转一圈，Kp为压力脉动系数

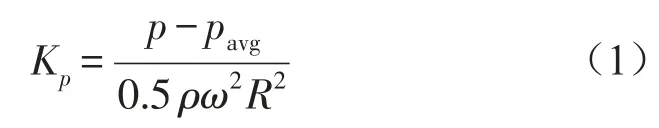
式中p为监测点的瞬时压强，pavg为监测点的时均压强，ρ和ω分别为流体密度和叶轮旋转角速度，R表示叶轮半径。

用Matlab进行快速傅里叶变换，可以得到各个频率对应的压力脉动系数Kp，引入无量纲频率系数St

式中f为频率，n，Z为叶轮每分钟的旋转速度和叶片数。根据此定义，St=1正好表示1倍叶片通过频率，而St=2表示为叶频的二倍频。

2 转速变化对流体激励的影响

由水泵相似理论可知，在叶轮几何参数不变的条件下，转速的提高有利于提高水泵的扬程。图3为不同转速（n=960 r/m in，1450 r/m in）下水泵的扬程和效率分布，计算工况从0.6到1.3倍的设计流量（Qs=300 t/h，450 t/h），叶片数为4。从图中可以看出，在所计算的流量范围内，扬程随着转速的提高而增加。根据相似理论，同一轴流泵运行在不同转速下，其扬程之比等于转速比的平方，即2.28。表1给出了两个转速下对应运行工况下的轴流泵扬程数值解的比值，随流量不同，数值解获得的比值并不为定值，在2.24～2.98范围内变化。从图3中还可以看出，在小流量工况下运行时，转速的变化对效率的影响很小，但随着流量的增加，水泵的效率有明显的增加。当流量从1.0Qs增加到1.3Qs，对应的效率分别增加了1%、8%。

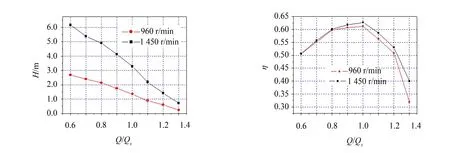
图3 不同转速下轴流泵的扬程与效率分布

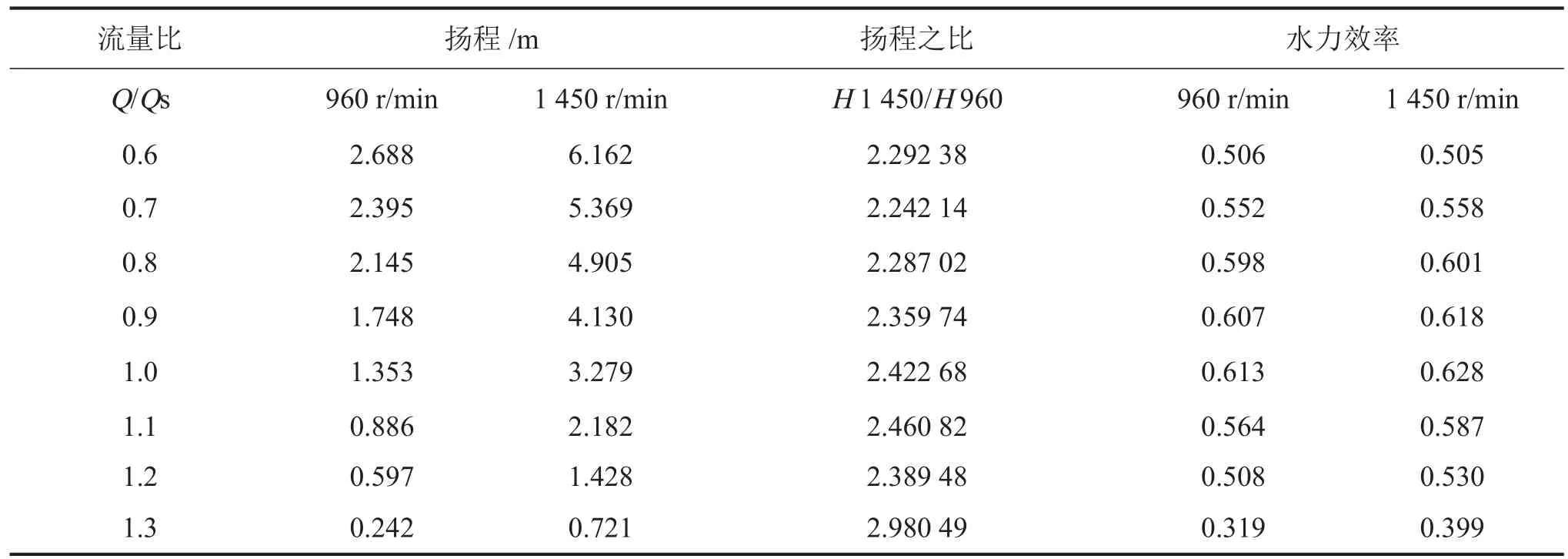
表1 不同转速下水泵扬程、效率及扬程之比

B1、B2和B3压力系数随转速的变化如图4所示，从图中可以明显看出，叶轮转速分别在1 450 r/m in时轴流泵内监测点B1、B2和B3的压力系数在频域的分布与转速960 r/m in、1.0Qs时的监测点压力系数相比，转速增加后，压力系数的频谱特性基本保持不变，主要的脉动能量集中在1倍谐频上，但是脉动幅度大增，在1倍叶频上，B1、B2和B3的压力系数峰值为0.208，0.198，0.047，远大于960 r/m in转速下的值。该图充分说明了转速对压力脉动程度的影响。

根据管内流动的相似准则，液体惯性力可以表示为

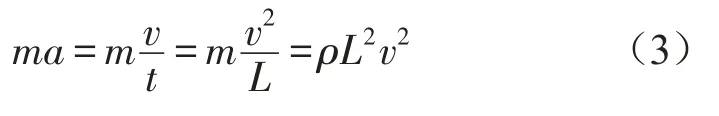
图4 额定流量下转速对B1，B2,B3压力系数的影响（Q/Q s=1.0）

图5是在额定流量下，轴流泵工作转速分别为960 r/min和1 450 r/m in时流体作用于叶轮的轴向力。可见随着转速的提高，叶轮轴向力的平均值和脉动幅值增大，从481.9 N增加到了1 988.84 N，其比值为4.13，并不等于转速比的平方(2.28)，压力脉动系数的均方根从6.56 N增加为25.19 N，比值为3.84。这表明转速改变后，即使工作在相似的工况点，轴流泵内的流动也不能达到真正地相似，从而使得叶轮受到的力偏离了相似理论的计算值。

3 流量变化对流体激励的影响

图6给出了B1、B2和B3三个监测点在0.6Qs、1.0Qs和1.3Qs流量时的压力系数的分布。从该图可以发现，B1、B2两点的压力脉动在三个运行流量下均呈现较好的周期性，脉动峰值均出现在1倍叶频及其高阶谐频上。从脉动幅度看，0.6Qs流量下各点的压力脉动最强，1.3Qs流量下压力脉动减弱，1倍叶频下的压力脉动系峰值如表2所示，可见，轴流泵流量从1.0Qs减小到0.6Qs，B2点的压力系数峰值增加了71%，而流量从1.0Qs增加到1.3Qs，B2点的压力系数峰值下降了51%。

图5 额定流量下转速对叶轮轴向受力的影响

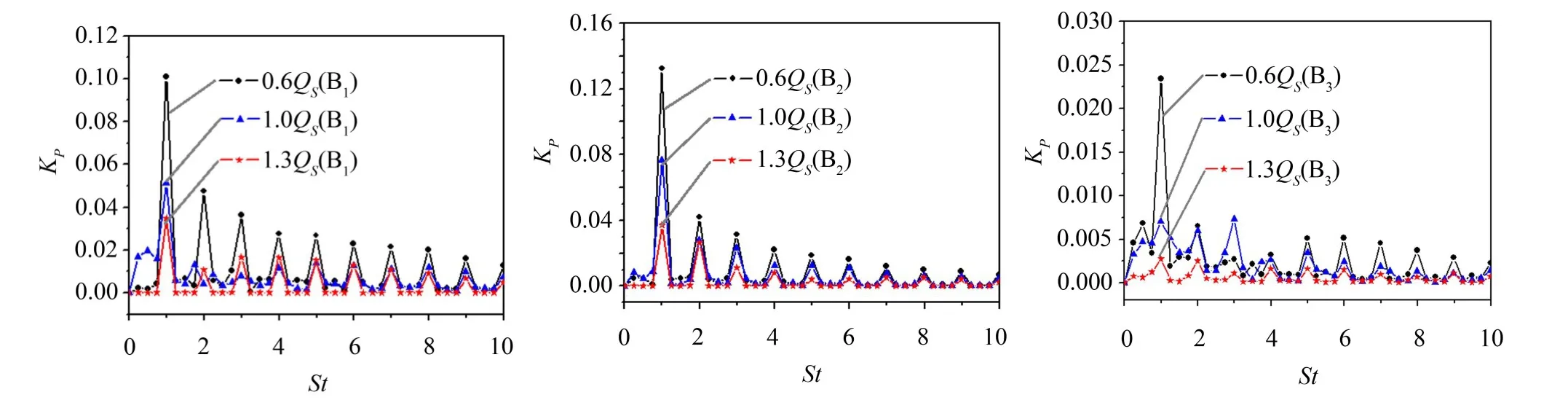
图6 运行流量对轴流泵内压力脉动的影响（B1、B2、B3）

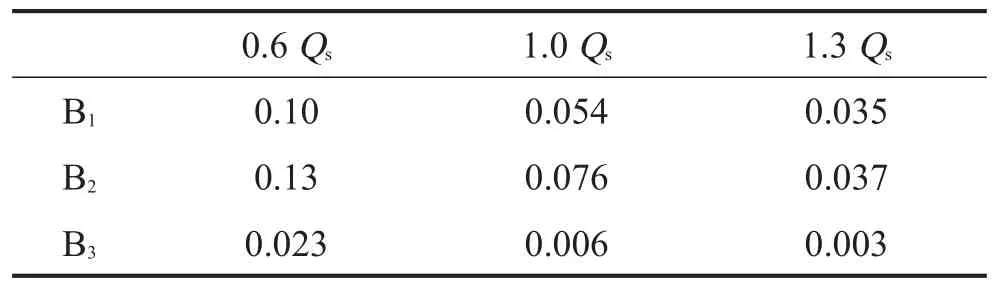
表2 监测点压力脉动系数的峰值(St=1)

图7给出了轴流泵运行在不同流量下尾迹区W1和W7、支撑架前缘V1和V7四点的压力脉动系数在频域的分布。该图表明，尾迹区W1和W7的压力系数峰值频率为叶频.。不过，当轴流泵工作在0.6Qs流量时，St=0.25处也出现了小的峰值。根据前面的流动分析可知，在0.6Qs流量时叶轮通道内出现了大范围分离，该分离流在尾迹区没来得及充分掺混，成为尾迹区的压力扰动源。该分离流流向下游的支撑架，与支撑架相互作用，引起绕支撑架的分离流动，从而使支撑架前缘的压力系数脉动峰值频率也偏离叶频，出现在St=0.25处。

图7 尾迹区与支撑架前缘区压力脉动系数随流量的变化

图8为叶轮在0.6Qs、1.0Qs和1.3Qs流量下受到的轴向力随时间的变化。可见随轴流泵流量从0.6 Qs变为1.3Qs，流体作用于叶轮的轴向力均值从947.3 N减小为84.3 N，轴向力随时间的脉动幅度也逐渐减小，其均方根从9.96 N减小为1.28 N。

4 结语

通过上述计算分析可以得知

转速改变后，即使工作在相同的工况点，轴流泵内的流动也不能达到正真地相似，从而使得叶轮受到的力偏离了相似理论的计算值；

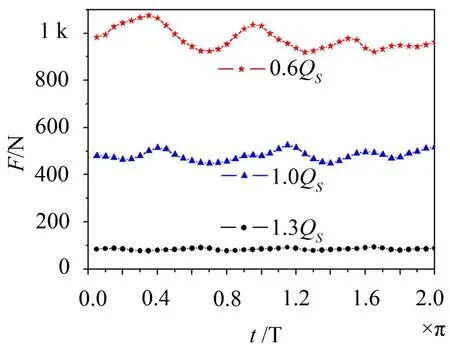
图8 不同流量下流体施加于叶轮的轴向力

在小流量时叶轮通道内出现了大范围分离，该分离流在尾迹区没来得及充分掺混，成为尾迹区的压力扰动源；

轴流泵工作在小流量时，泵内压力脉动与叶轮受力均大于大流量工况，不利于小流量工况下轴流泵流动噪声与振动的控制。

[1]陈长盛，马 俊，柳瑞锋，等.运行工况对离心泵振动影响的试验研究[J].噪声与振动控制，2012，32(12)：199-202.

[2]施卫东，李启锋，陆伟刚，等.基于CFD的离心泵轴向力计算与试验[J].农业机械学报，2009，40(1)：60-63.

[3]沙 毅，宋德玉，段福斌，等.轴流泵变转速性能试验及内部流场数值计算[J].机械工程学报，2012，48(6)：187-192.

[4]王 晶，冯 涛，刘 克，周启君.离心泵流动噪声与其水力学参数关系的实验研究[J].流体机械，2007，35(5)：8-11.

[5]陈长盛，杨爱玲，李国平，等.叶片数变化对轴流泵流体激励力影响[J].噪声与振动控制，2013，33(3)：55-59.

Research of Fluid Excitation of Axial Flow Pump under Different Working Conditions

ZHANG Shuo1,CHEN Chang-sheng2

(1.Naval Deputy Office in 704 Research Institute,Shanghai 200031,China; 2.704 Research Institute,China Shipbuilding Industry Corporation,Shanghai 200031,China)

Abastract:Structural vibration of a pump is partly caused by pressure pulsation of unsteady flow in the pump,the change of flow field w ithin the pump is caused by the change of working conditions,and the vibration characteristics of the pump w ill be affected.In this paper,the unsteady flow field of an axial flow pump is simulated by means of FLUENT software w ith the steady flow as the initial field.The results of excitation force of flow on the pump and the impeller is calculated and analyzed under different working conditions.The results show that pressure pulsation on the blade deviates from the calculation data based on the sim ilarity theory when rotating rate changes.With the flow rate decreasing,the pressure pulsation w ill increase,and separate flow w ill occur in the impeller area.

vibration and wave;working conditions;axial flow pump;pressure pulsation

1006-1355(2014)04-0134-04+152

TB53；O422.6 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.029

作为最常用的设备之一，泵在运行时经常会根据需要调节运行工况。而不同的运行工况会产生不同的流动情况，致使泵体振动情况发生变化[1]。流体激励是引发泵体振动的主要激励源之一，其受运行参数的影响也不能忽视。文献[2]中讨论了泵内流场轴向力的计算方法，得到了全工况下的叶轮轴向力分布，并与试验值有较小的误差；文献[3]对某轴流泵进行了变转速的性能计算与试验，提出了轴流泵内部轴向运动雷诺数小是使得其不能满足相似定律的主要原因；文献[1]和文献[4]则偏重于试验，分别研究了转速、流量变化和进出口压力变化对振动的影响；文献[5]则是通过理论计算研究了叶轮形式对流体激励力的影响。现有研究成果中，还鲜有流体激励力受运行工况影响的研究。为此，本文以一台立式轴流泵为研究对象，通过理论计算来研究运行参数与泵内流体激励力的关系，为建立低噪声泵水力设计方法提供一定的参考。

1 轴流泵流体计算模型

2014-02-11

张 硕(1977-)，男，江苏宜兴人，硕士。目前从事舰船设备过程控制及振动噪声控制的研究。

E-mail:jzzx704@163.com