无拆卸轴承刚度测试方法的研究

蒋爱华，符栋梁，代学昌，周 璞，华宏星

（1.中国船舶重工集团公司 第704研究所，上海200031；2.上海交通大学 机械系统振动国家重点实验室，上海200240）

无拆卸轴承刚度测试方法的研究

蒋爱华1，2，符栋梁1，代学昌1，周 璞1，华宏星2

（1.中国船舶重工集团公司 第704研究所，上海200031；2.上海交通大学 机械系统振动国家重点实验室，上海200240）

轴承刚度对轴系振动有重要影响，研究无拆卸轴承刚度测试方法有利于快速可靠地了解轴系的振动特性。通过机架安装隔振器、泵进出口安装波纹管、电机与泵转子间采用电磁联轴器等结构措施；构建了离心泵转子-滚动轴承的试验台架。以光电传感器安装位置为转轴相位参考，通过转轴振动位移峰值识别出轴承截面轴系等效偏心质量的相位。通过附加质量于等效偏心质量相位产生激振力，并运用Lab VIEW构建的虚拟仪器测量附加质量前、后振动位移峰值变化量，从而得出轴承刚度。最后通过台架实际配置与转子模型进行了验证。结果表明，轴承刚度无拆卸测试方法有效可行，设计的试验台架可实现附加配重的安装，并能够有效地予以验证；所构建的虚拟仪器也能够准确计算得出转轴偏心质量相位与轴承支撑刚度。

振动与波；滚动轴承；刚度；无拆卸；光电传感器；离心泵

轴承的支撑刚度对轴系振动至关重要，转子动力学建模中其准确性将直接决定分析结果的可信度，因此轴承模型的简化与参数的测试[1—3]在学术和工程中就引起了为数不少的研究和关注。

滑动轴承常根据具体结构形式的不同，被简化成八个油膜刚度与阻尼系数[4,5]（固定瓦径向滑动轴承）或者16个油膜刚度与阻尼系数[6,7]（可倾瓦径向滑动轴承），针对不同滑动轴承已有专用的转子-轴承试验台架。

与滑动轴承相比，滚动轴承运转过程中动力特性更加复杂（滚动轴承是一种高载荷流体动力摩擦副，不仅存在固体接触弹性变形，还有流体动力润滑油膜的影响，且二者又相互耦合），迄今尚无系统、完整的滚动轴承动力特性分析方法[8]，因此轴承参数的测试至关重要。

现有滚动轴承处理方式一是将其简化为完全刚性支撑，二是简化为弹性支撑并按经验公式估算其参数[9,10]。

完全刚性支撑简化对柔性转子是可行的，对于刚性转子—支撑系统则过于粗糙，此时轴承刚度的测试可在非旋转状态下外加激励力测得。

简化为弹性支撑时，其阻尼因较小而常被忽略，其刚度则可采用转子支撑系统频响特性确定轴承特性的方法[11，12]、定转速滚动轴承动力特性测试法[13]得出。

滚动轴承动力特性直接影响转子支撑系统的动力特性，即临界转速与频响特性等，采用已知的标准转子安装在待测轴承上，测定其临界转速和频率响应，则可反算被测轴承的等效刚度与等效阻尼。

这种测试方法的缺陷在于若轴承与转子刚度较大则系统临界转速将较高，而转轴转速无法满足要求，且这种方法需要标准测试台架而无法在现场得出轴承参数，台架的安装也需较长时间。

定转速滚动轴承动力特性测试法即在一固定转速下用锤击法激励轴承得出该转速下的频响特性，这种方法与锤击静止轴承测阻抗的方法相比，消除了轴承内游隙的作用，更接近于实际工作情况[14,15]。

但其缺陷在于所施加激励只能是某一定向力，这与轴承工作中主要受与转子同步旋转的不平衡激励力有根本区别，因此所得轴承刚度也有一定误差。

鉴于以上原因，本文提出一种无拆卸滚动轴承刚度测试方法，并以离心泵转子支撑系统为对象进行轴承刚度的测试。

1 轴承刚度测试原理

将滚动轴承也简化为弹簧支撑，其刚度测试方法基于虎克定理，即在支撑处施加外激励力，同时测得该激励力大小与支撑处转轴的位移变化量，从而得出其位移阻抗并得知支撑刚度。测试中支撑刚度计算表达式如式（1）所示

式中F为外加激励力幅值，Δx为外加激励力后振动位移峰值的变化量。

采用在转轴上附加质量的方法，则F=meω2，其中m为附加在转轴上的质量，e为附加质量处转轴半径与附加质量重心至转轴外表面距离之和，ω为转轴转速。这些参数可从称重天平、转轴实际结构与运转工况中得出。

Δx则可通过振动位移传感器测量附加质量前后，转轴附加质量处振动位移的变化量得出。通过以上方式则可以实现轴承的无拆卸测试。

需要注意的是，附加质量在转轴圆周上的安装位置需要与转轴截面等效偏心质量相位相同。

这是因为即使经过精密动平衡修正后的转轴自身仍具有偏心质量的存在，当转子支撑系统无阻尼影响，振动位移传感器测得最大振动位移处的相位转子自身轴承处截面等效偏心质量相位。

若附加质量与该偏心质量同相位，则测得振动位移将增大且峰值相位不变；若附加质量与该偏心质量相位不同，则测得振动位移可能变大也可能变小，峰值相位将变化，虽然能够测出振动位移峰值变化量Δx，但实际激振力F则无法得出，如图1（b）中所示，从而无法得出轴承刚度。

如图1所示为转轴截面不同位置附加质量的受力分析与轴承刚度测试原理图，其中图1（a）为本文中测试原理图。

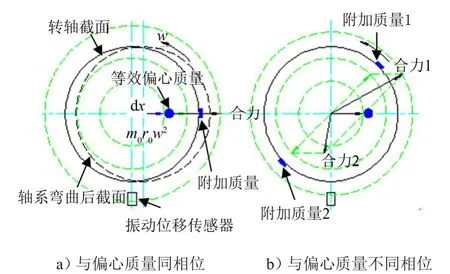
图1 轴系受力分析与轴承刚度测试原理

2 测试台架

设计离心泵轴系试验台架，轴系安装情况如图2所示，整个轴系试验台架竖直安装，垂直于轴系机架方向为图中的+X向。

电机通过非接触式电磁联轴器带动轴系与离心泵叶轮转动，轴系、电机与离心泵安装与同一机架上，机架通过八个隔振器安装于刚性基础上。

离心泵通过管道吸入水并将水送回到水箱中，进出口通过波纹管与管道相连接以隔离管道振动，从而使电机—轴系—离心泵—机架成为一个独立的振动系统。

电磁联轴器的作用是仅传递扭矩而消除电机转轴与模拟轴系不对中引起的系统振动，通过动平衡技术减小了电机主轴的质量不平衡。

其中叶轮端安装有一个滚珠轴承，即轴承2，联轴器端紧靠安装有两个与叶轮端完全相同的滚珠轴承，即轴承1。

3 转轴等效偏心质量相位

测试转轴初始等效偏心质量相位时，须设定零相位作为参考。

本文采用了反光式光电传感器进行初始相位的识别，电磁联轴器上固定反光片作为零相位。当光电传感器发射出的射线被反光片反射至传感器接收装置时，光电传感器输出高电平。

如图3（a）所示为传感器的实际安装布置情况。以光电脉冲传感器的脉冲信号上升沿为起始相位，转子每转动一周则产生一个方波脉冲信号；4个位移传感器分别布置于两个轴承附加的X方向与Y方向，用于测试转轴的振动位移，传感器基座固定于支架上，振动加速度传感器则用于测试离心泵支架的振动加速度。采用LMS系统对各传感器进行同步数据采集，采样率为20 480 Hz，共采集了5 s内的转子的振动位移信号与光电传感器的脉冲信号。

如图3（b）、（c）所示分别为联轴器端、离心泵端+ X向振动位移信号与光电传感器脉冲信号0.1 s内的波形，测试时电机转速为2 930 r/m in。

由于已知两个脉冲信号上升沿的时间间隔内，离心泵转子的转角为360度，假定两个脉冲信号上升沿时间间隔内转子保持匀速转动，因此可由图3（b）、（c）中振动位移波峰值点与光电传感器脉冲上升沿的时间差，得出等效偏心质量的相位差。

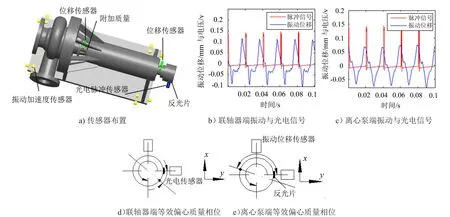
图3 等效偏心质量相位测试

振动位移波峰值通过以下方式识别：以0.5倍最大振动位移值为阈值，识别出各大于阈值连续数据段中的最大值即为波峰值。

以上算法通过Lab VIEW编写完成，如图3（d）、（e）所示即为计算的最终结果。

将5 s内振动位移波峰值与脉冲上升沿的相位差进行了算术平均，最终得出联轴器端X向最大振动位移处与反光片夹角为–40.27度，而离心泵端X向最大振动位移处与反光片之间夹角为164.766度。

4 轴承刚度的测试

基于测得最大位移相位，先后在联轴器端与离心泵端轴承处安装附加质量，并测出安装附加质量后轴系的振动位移，则可得出轴承刚度。

以质量偏心的卡环为附加质量安装于轴系靠近轴承位置处。以反光片轴向中心线为零相位参考，安装卡环前首先周向粘贴刻度胶带，并将某一刻度与反光片中心线对齐，胶带最小刻度为1 mm。

轴承安装位置轴径为28 mm，转角40.27度对应周向长度9.8 mm，转角164.766度对应周向长度40.3 mm，安装时以卡环对称中心安装于相应周向位置处，以保证附加质量安装相位与联轴器端或离心泵端等效偏心质量相位相同。

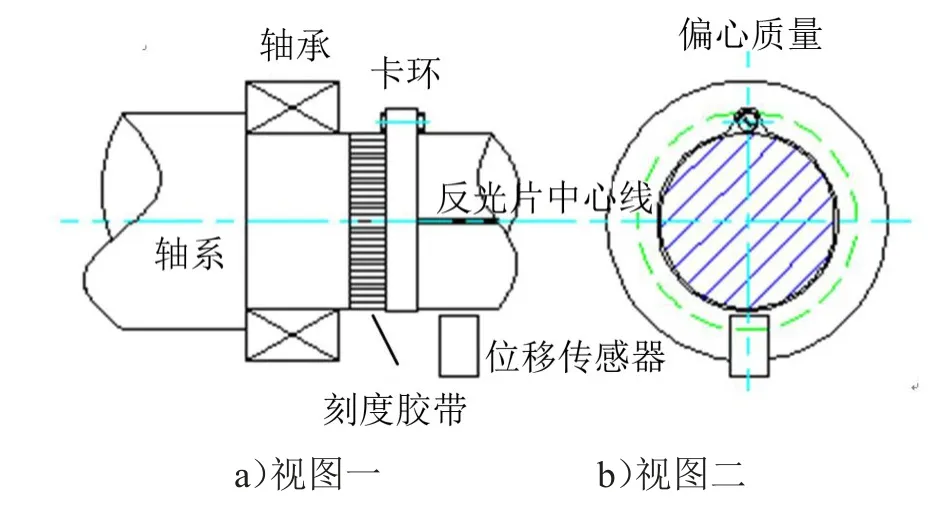
图4 偏心质量的安装示意图

将重14 g的配重安装于联轴器端等效偏心质量的相位处，亦即–40.27度处，控制轴系以转速2 930 r/m in转动，同时以等效偏心质量相位测试系统中的数据采集系统测量了5 s内轴系的振动位移。

将增加配重后5 s内轴系振动位移的波峰值进行了算术平均，并减去增加配重前5 s内轴系振动位移波峰值的算术平均值，以得到联轴器端轴系增加配重前、后的幅值差。

而后拆卸联轴器端配重，安装11.6 g配重于离心泵端，通过以上所述相同方法得出离心泵端轴系增加配重前、后的幅值差。

增加配重后激振力幅值通过“轴承刚度测试原理”中介绍方法，亦即F=meω2得出。

以上测试中，数据采集系统参数设置与转轴初始等效偏心相位测试的参数设置相同。

如图5（a）、（b）所示即为联轴器端、离心泵端分别增加附加质量前后的+X向振动位移传感器波形，从图中可以看出，联轴器端、离心泵端分别增加附加质量后，其振动位移均有一定增大。

在得出激振力幅值与幅值差后，则可根据式（1）得出轴承的刚度。轴承刚度计算的结果如表1中所示。

5 测试结果的验证

从表1中可以看出，测得联轴器端支撑刚度接近离心泵端支撑刚度的两倍，这与联轴器端安装两个与离心泵端相同型号轴承的实际结构相吻合。

此外，通过建立测试台架的转子动力学模型，并将测得两轴承处支撑刚度代入模型中进行计算，最后对比计算所得测试台架振动与测试所得台架振动以验证测得轴承支撑刚度。

根据测试台架实际结构建立了包含转轴、离心泵叶轮、轴承、电机、机架四圆盘三轴段的+X方向转子动力学模型如图6（a）中所示。

图5 轴系振动位移测试

其中圆盘m4为离心泵叶轮，其余圆盘均根据转轴实际结构简化得出，kx2与kx3即分别为联轴器端、离心泵端轴承刚度，m0包含电机、泵体、机架的质量，kx0为隔振器刚度。

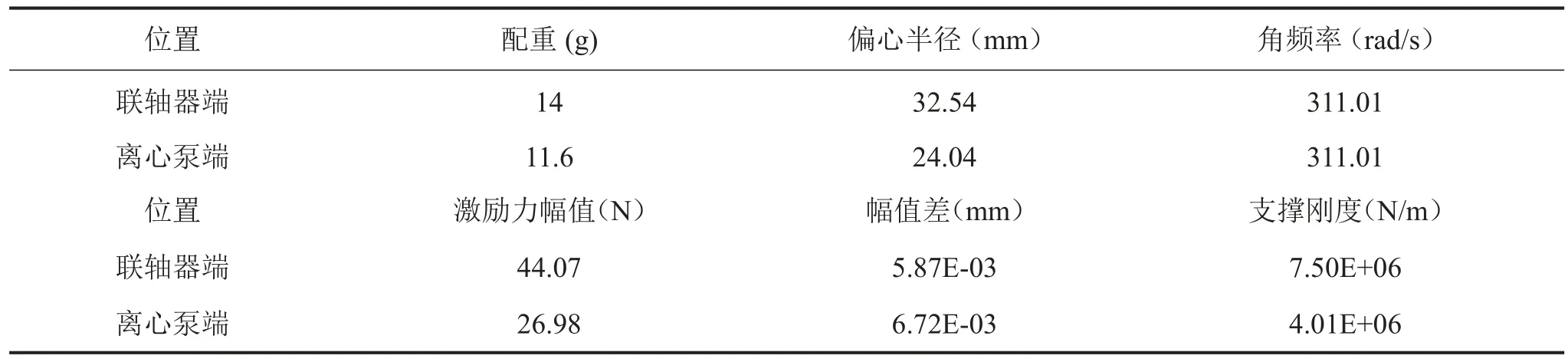
表1 轴承刚度计算

通过CFD计算所得转动过程中离心泵叶轮上所受流体力作为激励力，与测得轴承刚度共同代入所建立的转子动力学方程中，可得m0的振动位移如图6（b）中虚线所示。

图6（b）中实线所示为图3（a）中所示振动加速度积分后平均的结果。

从图6（b）中可以看出计算所得m0振动位移与测得机架振动位移趋势基本相同。

需要指出的是，轴系多点支撑对附加质量产生轴承处的激励力有一定影响，可建立二自由度系统通过多次附加不同配重于轴系同一截面不同相位处，并分析振动位移幅值与相位的变化，可得轴承处的初始等效偏心质量大小，也可获得更加准确的轴承刚度。

图6（b）中计算值与测试值之间的差值还包含了CFD计算的误差、模型简化的误差、电机不平衡质量激励力等的影响。

此外，改变振动位移传感器垂直安装的相位可得出轴承不同周向位置的支撑刚度，可测非周向同性轴承的刚度。

综上所述，测试所得轴承刚度结果满足工程要求，所提出的无拆卸轴承刚度测试方法是可行的。

6 结语

通过以上分析，可得如下结论：

(1)提出了一种轴承刚度测试方法，能够在不拆卸转子系统的前提下得出滚动轴承的支撑刚度，该方法有效可行；

(2)设计了离心泵转子试验台架，能够有效验证无拆卸轴承刚度测试方法的有效性；

(3)构建了轴承刚度测试虚拟仪器，能够准确计算得出轴承偏心质量相位与支撑刚度；

(4)以光电传感器安装位置为轴系参考相位，能够准确得出轴系等效偏心质量的相位，并实现附加配重的安装；

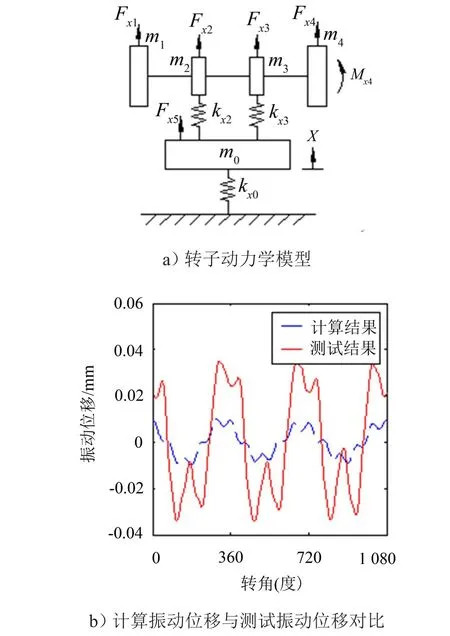
图6 轴承刚度测试结果验证

(5)本文中卡箍上的配重与轴承存在一定轴向距离，若能够构造修正算法消除该轴向距离的影响，所得结果将更加准确。

[1]方 兵，张 雷，曲兴田，赵 继.角接触球轴承动力学建模与实验[J].农业机械学报，2012，43(6)：215-219.

[2]De Santiago O,San Andrés L.Experimental identification of bearing dynamic force coefficients in a flexible rotor further developments[J].Tribology Transactions,2007,50 (1):114-126.

[3]孙炳南，谢 帆，荆建平.轴承支撑特性对轴系稳定性影响[J].噪声与振动控制，2012，32(6)：137-140.

[4]Su J.C.,Lie K.N.Rotor dynam ic instability analysis on hybrid air journal bearings[J].Tribology International, 2006,39(3):238-248.

[5]姚大坤，黄文虎，邹经湘.滑动轴承油膜刚度参数的识别[J].动力工程学报，2005(8)：483-486.

[6]杨金福，杨晟博，杨 昆，付忠广.滑动轴承转子系统刚度和阻尼性质的分析与探讨[J].振动与冲击，2006(8)：179-182.

[7]Wale G.D,Mba D.Identifying and m inimising uncertainty for experimental journal bearing studies[J].International Journal of Rotating Machinery,2005(3):221-231.

[8]闻邦椿，等.高等转子动力学[M].北京：机械工业出版社，2000.

[9]吴 昊.滚动轴承特性及轴承—转子系统动力学模型研究［D］.上海：华东理工大学博士学位论文，2011.

[10]林腾蛟，荣 崎，李润方，邵毅敏.深沟球轴承运转过程动态特性有限元分析[J].振动与冲击，2009(1)：118-122.

[11]杜 蛟.机床主轴系统支承动态参数识别方法的研究[J].机械强度，1994(6)：22-31.

[12]付才高.航空发动机强度设计、试验手册：转轴系统振动试验[M].北京：航空工业出版社.1987，2.

[13]黄太平，罗贵火，苏卫民，等.滚动轴承动力特性测试方法[J].振动测试与诊断，1996(4)：33-39.[14]黄太平，田淑芳.弹性支撑动态特性分析与试验[J].南京航空学院学报，1983，(3)：22-36.

[15]周 瑾，倪佐僖.基于不平衡响应的磁悬浮轴承刚度阻尼辨识方法研究[J].振动与冲击，2013，32(3)：29-34.

Study on Measurement Method of Bearing Stiffness w ithout Disassembling

JIANG Ai-hua1,2,FU Dong-liang1,DAI Xu-chang1, ZHOU Pu1,Hua Hong-xing2

(1.704 Rsearch Institution,China Shipbuilding Industry Corporation,Shanghai 200031,China; 2.State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University, Shanghai 200240,China)

Bearing stiffness has significant influence on shaft vibration.Study on the measurement method of bearing stiffness w ithout disassembly is beneficial for obtaining the shaft vibration effectively and reliably.A workbench w ith a centrifugal pump rotor and rolling bearings is made by installing vibration isolator on brace,mounting corrugated pipe at pump’s inlet and outlet,and electromagnetic coupling between the motor’s shaft and the pump’s shaft.A lso,photoelectric sensors are installed as a shaft phase reference,and phase angles of the equivalent eccentric weights on shaft sections near the bearings are identified by the displacement peaks of the shaft vibration.Then,excitation forces are generated by adding masses on the shaft at the phase angles,and variations of the vibration-displacement peaks as well as the bearing stiffness are tested by virtual instrument built by LabVIEW.Finally,the stiffness is validated by actual workbench configuration and the rotor model.The result shows that the bearing stiffness test method w ithout disassembling is feasible,the workbench is reliable to validate the method,and the virtual instrument can also accurately calculate the equivalent eccentric weight’s phase of the shaft and the support stiffness of the bearing.

vibration and wave;rolling bearing;stiffness;w ithout disassembly;photoelectric sensor;centrifugal pump

1006-1355(2014)04-0128-06

TB53 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.028

2013-09-20

蒋爱华，男，博士，主要从事流体激励诱发振动方面的研究。

E-mail:jiang198011@163.com

华宏星，教授，博士生导师，主要从事机械系统振动、噪声与冲击研究。

E-mail:hhx@sjtu.edu.cn