流体载荷对水下自由阻尼板阻尼损耗因子的影响

尹帮辉，王敏庆

（西北工业大学 航海学院，西安710072）

流体载荷对水下自由阻尼板阻尼损耗因子的影响

尹帮辉，王敏庆

（西北工业大学 航海学院，西安710072）

结构的阻尼损耗因子是潜艇降低水下辐射噪声的重要参数。为此，采用谱有限元法以计算流体载荷作用下的自由阻尼板的结构损耗因子，探讨辐射损耗因子同功率转换系数间的关系；然后使用谱有限元法比较了含流体和不含流体的自由阻尼板的结构损耗因子的差异，使用能量法对相关计算结果进行验证；最后使用三维模型对流体载荷作用下的自由阻尼板的功率转换系数进行了计算，进而分析功率转换系数同阻尼层杨氏模量、阻尼层厚度、阻尼层材料损耗因子等参数的关系。研究发现：在低于第二阶弯曲波产生频率的频段范围内，无流体时的损耗因子小于有流体的自由阻尼板；从频段平均的角度来看，功率转换系数在低频存在较大峰值，在高频变化较为平缓且数值较小；实际潜艇在流体载荷下主要通过改变结构的阻尼来改变其辐射的阻尼损耗因子。分析结果对于潜艇结构阻尼的优化设计有参考价值。

振动与波；流体载荷；自由阻尼板；阻尼损耗因子；谱有限元法；三维弹性理论

水下自由阻尼板的阻尼损耗因子分为结构损耗因子和辐射损耗因子两部分，本文分别对这两部分内容进行研究。首先，流体载荷的作用会改变振动系统应变能分布，从而改变其结构损耗因子。对于多层板，谱有限元法[7]是一种计算其结构损耗因子的常用方法，该方法使用有限元法来计算波的传递特性，根据得到的特征波形使用应变能法计算各阶波的损耗因子，但是由于该方法并不考虑流体载荷，所以不能用于计算流体载荷作用下的自由阻尼板的结构损耗因子。本文在文献[7]的基础上使用质量单元模拟流体载荷的作用，将其用于研究考虑流体载荷的自由阻尼板的结构损耗因子。其次，流体声辐射将产生辐射损耗因子，直接测量或者计算辐射损耗因子比较困难，所以拟使用功率转换系数对辐射损耗因子进行间接的研究。功率转换系数定义为辐射功率和输入功率的比，同时它也描述了辐射损耗因子占阻尼损耗因子的比例，所以如果能通过计算得到输入功率和辐射功率，那么就可以得到功率转换系数。目前对水下自由阻尼板的声辐射特性计算用的比较多的方法有局部作用模型[8]和三维弹性模型[9，10]，以下的理论介绍及分析均使用三维弹性模型进行数值仿真，计算得到简谐激励下的自由阻尼板的功率转换系数。

本文首先探索了谱有限元法以计算流体载荷作用下的自由阻尼板的结构损耗因子，探讨了辐射损耗因子同功率转换系数间的关系。然后，使用谱有限元法比较了含流体和不含流体的自由阻尼板的结构损耗因子的差异，使用能量法对相关计算结果进行了验证。最后，使用三维弹性模型对流体载荷作用下的自由阻尼板的功率转换系数进行了计算，讨论了功率转换系数同阻尼层杨氏模量、阻尼层厚度、阻尼层材料损耗因子等参数的关系。

1 基本理论

阻尼损耗因子反映了结构振动时的耗能特性，对于水下振动的自由阻尼板，其阻尼损耗因子由结构损耗因子ηs和辐射损耗因子ηr两部分组成，即

其中结构损耗因子主要来源于阻尼材料将振动能量转化为热能耗散掉，辐射损耗因子主要来源于流体的声辐射。

1.1 结构损耗因子

谱有限元法[7]是一种分析无限介质中波传播特性的有限元方法，它使用直线单元的线性形函数对位移场进行离散，将离散形式的位移场代入拉格朗日原理的公式中得到特征方程，对特征方程进行求解得到某频率下的各阶波的特征波数和特征波形，对特征波形使用应变能法得到该波形的结构损耗因子。谱有限元法的特征方程可简化为

其中A为含有频率的矩阵，当频率固定为某一数值时，该矩阵为一常矩阵，q0为节点振动位移向量，q1为节点振动速度向量，k为波数。方程(2)为以k为特征值，[q0q1]T为特征向量的特征方程，对其进行求解可以得到特征波数和特征波形。图1作出了使用文献[5]的谱有限元法对自由阻尼板进行网格划分的单元、节点划分示意图。谱有限元法中的单元为含有两个节点的线单元，每个节点含有3个方向的振动位移自由度。

图1 谱有限元单元、节点划分示意图

由于谱有限元法没有考虑流体载荷的作用，所以不能用来分析水下自由阻尼板的结构损耗，这是本文进行探索的主要问题。流体载荷对振动的自由阻尼板的作用力可分为惯性力和阻尼力[12]，其中对应变能分布产生影响的主要是惯性力。自由阻尼板的振动将带动附近流体也一起振动，流体质量的反作用力对改变原来自由阻尼板的应变能的分布，从而改变其结构损耗因子。本文忽略流体阻尼力对应变能分布产生的影响，使用谱有限元法将流体载荷离散为质量单元。图2作出了考虑流体载荷的谱有限元单元、节点划分示意图，其中m表示基底层划分的单元数，n表示阻尼层的划分的单元数，z方向表示自由阻尼板厚度方向。

流体质量载荷[12]的大小主要取决于自由阻尼板的弯曲波波长，波长越长，质量载荷越大。附加于自由阻尼板表面的质量面密度可表示为

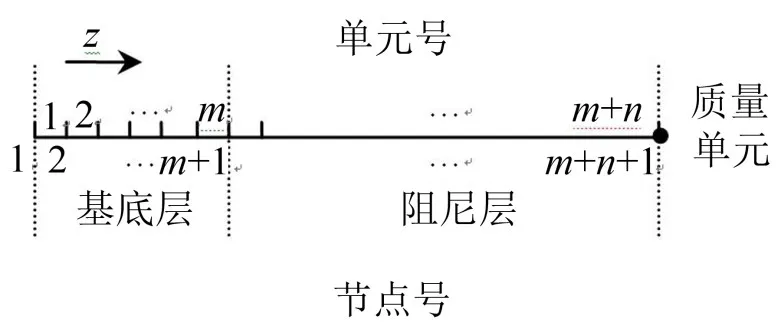
图2 考虑流体载荷谱有限元单元、节点划分示意图

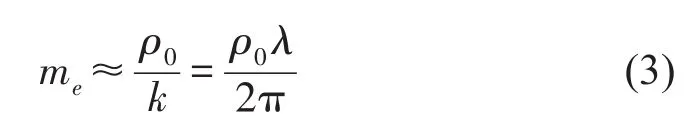
其中k为自由阻尼板中弯曲波波数，ρ0为流体密度，λ为自由阻尼板中弯曲波波长。使用拉格朗日原理将流体质量载荷化为质量单元，其质量单元的单元矩阵为一常数，即式中的me。

当自由阻尼板的基底层较厚时，其弯曲波波长和只考虑基底层的弯曲波波长差别不大，所以可以直接使用基底板的弯曲波波长来计算流体质量单元的单元矩阵。这种方法为直接谱有限元法。

当基底层较薄或者当阻尼层杨氏模量较小时，使用直接谱有限元法将会导致较大误差。前者是因为当基底层较薄时，自由阻尼板的弯曲波波长和基底层的弯曲波波长差别较大；后者是因为当阻尼层杨氏模量较小时，结构损耗因子对流体载荷的变化很敏感，所以需要较精确的计算自由阻尼板的弯曲波波长。流体载荷的大小跟自由阻尼板弯曲波长有关系，而自由阻尼板的弯曲波长又同流体载荷的大小有关系，所以一般使用迭代算法来求流体载荷和弯曲波长，根据文献[13]的思路，使用图3所示的迭代算法，图中kb为迭代法的迭代初值，取为基底板弯曲波波数，其中“根据k1计算出流体载荷大小”所使用的方法为式。本文称这种方法为迭代谱有限元法。

能量法[14]是一种使用一周期振动损耗的振动能量和总的机械振动能量的比值来描述损耗因子的方法。使用能量法可将水下自由阻尼板的结构损耗因子表示为

其中Pin是输入功率，Prad是声辐射功率，ω是激励角频率，E1是基底层应变能，E2是阻尼层应变能。本文第二节使用能量法的计算结果作为参考值对相关方法进行验证，其输入功率和应变能来自于ANSYS谐响应分析。

1.2 辐射损耗因子

辐射损耗因子来源于流体中的声辐射所带来的功率损耗，使用功率转换系数对其进行研究。功率转换系数用来表示声辐射功率占输入功率的比例，即

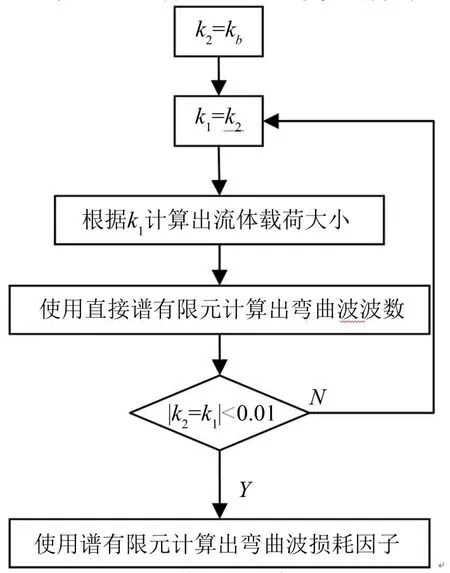
图3 迭代谱有限元法流程图

根据能量法，功率转换系数同结构损耗因子ηs和辐射损耗因子ηr存在如下关系

从式可以看出：功率转换系数描述了辐射损耗因子占阻尼损耗因子的比例。所以可以使用功率转换系数来研究辐射损耗因子的变化规律。

为了计算功率转换系数，需要得到输入功率和声辐射功率，利用文献[9]描述的三维弹性模型可以比较容易地得到上述两个参数，并进而计算得到功率转换系数。三维弹性理论将位移场分解为纵波和剪切波的叠加，纵波使用标量势Φ描述，剪切波使用矢量势ψ描述，即

假设基底层为四边简支的Love-Kirchhoff薄板，其振动位移可以表示为三角函数叠加的形式，即

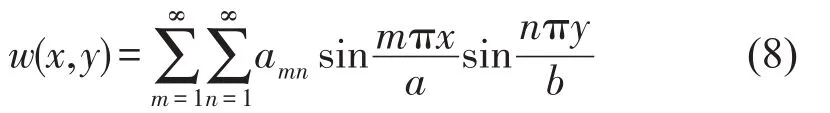
其中a、b为矩形平板的两条边长。

使用三维弹性模型来描述阻尼层的振动。阻尼层的边界条件如图4所示：阻尼层同基底层是粘结在一起的，所以接触面上三个方向位移相同；阻尼层另外一表面是同流体相接触的，该阻尼层该接触面的法向位移和流体一致，同时阻尼层该接触面处的法向正应力同流体在该处的声压一致；阻尼层的另外四个侧面假设其面内位移为零法向自由。在以上边界条件下，阻尼层标量势函数和矢量势函数都可表示为三角函数的叠加，即

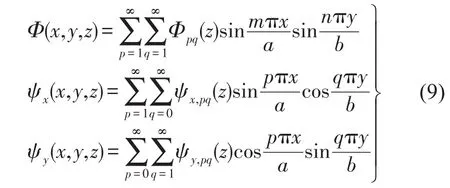
其中Φpq(z)、ψx,pq(z)、ψy,pq(z)为关于坐标z的函数，三者均可表示为三角函数叠加的形式，即

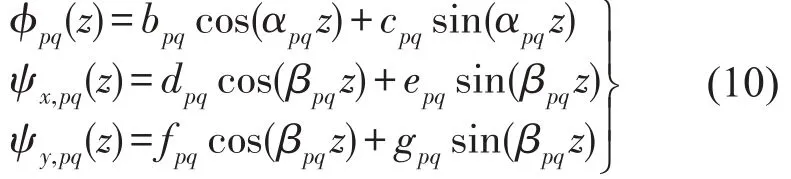
其中

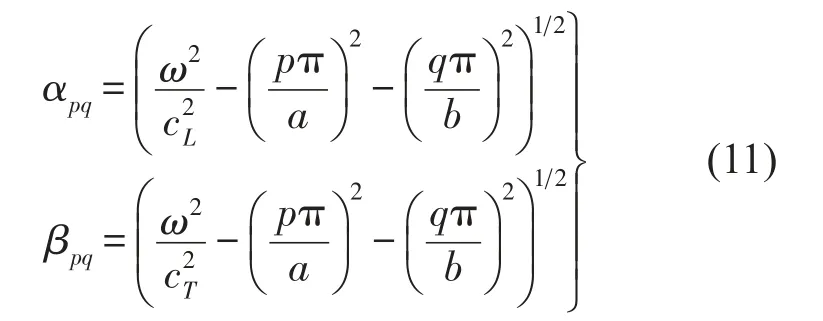
另外ψz可以由ψx和ψy表示出来。

在式中，amn、bpq、cpq、dpq、epq、fpq、gpq为未知数。根据各接触处的位移连续条件、载荷连续条件以及所施加的简谐载荷可以列出线性方程组，对线性方程组进行求解得到这些未知数，将这些未知数再代入上式可以求得基底层的振动速度、阻尼层的势函数，根据阻尼层势函数可以得到阻尼层的振动速度等变量，并进而求出输入功率、声辐射功率，具体求解方法参考文献[6]。

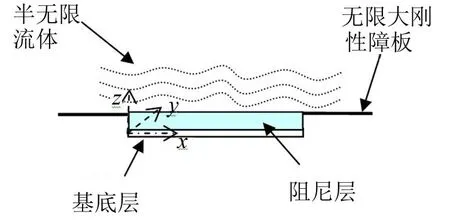
图4 水中自由阻尼板声辐射的三维弹性模型

2 结构损耗因子分析

流体载荷通过改变自由阻尼板的应变能分布从而改变其结构损耗因子。本节使用1.1节中提出的直接谱有限元法和迭代谱有限元法对流体载荷作用下的自由阻尼板的结构损耗因子进行计算，同时使用文献[7]中的谱有限元法对无流体载荷的自由阻尼板的结构损耗因子进行计算，对两种情况的结构损耗因子大小进行对比。为了验证计算结果的正确性，使用式的能量法分别对两种情况的结构损耗因子进行计算。

谱有限元法对考虑流体载荷和不考虑流体载荷两种情况下的自由阻尼板的结构损耗因子进行对比分析，其中无流体情况使用，有流体情况使用本文提出的。

谱有限元分析的参数如下：基底层材料为钢，杨氏模量E1=2.1×1011Pa，忽略其材料损耗因子，密度 ρ1=7 850 kg/m3，泊 松 比 ν1=0.3，厚 度h1=10 mm。阻尼层材料为橡胶，杨氏模量为E2=3×108Pa(直接法)或108Pa(迭代法)，损耗因子η2=0.1，密度为ρ2=1 200 kg/m3，泊松比ν2=0.4，厚度为h2=50 mm。流体介质为水，密度ρ0=1 000 kg/m3，声速c0=1 500 m/s。为验证谱有限元计算结果的正确性，使用ANSYS作谐响应分析，然后使用能量法计算结构损耗因子，ANSYS谐响应分析使用基底层为矩形的自由阻尼板平板，长和宽为a=b=0.6 m，一垂直于板的简谐点力作用在x0=0.2 m，y0=0.25 m处。

当阻尼层杨氏模量较大时，可以使用直接谱有限元法进行计算。下面对阻尼层杨氏模量E2=3×108Pa进行分析，图5作出了使用谱有限元、直接谱有限元法和能量法得到的分别处于流体中和真空中的自由阻尼板的结构损耗因子曲线。从图5可以看出：有流体和无流体情况下的谱有限元计算结果均和相应的能量法计算结果接近，这说明使用质量单元描述流体载荷是可行的。

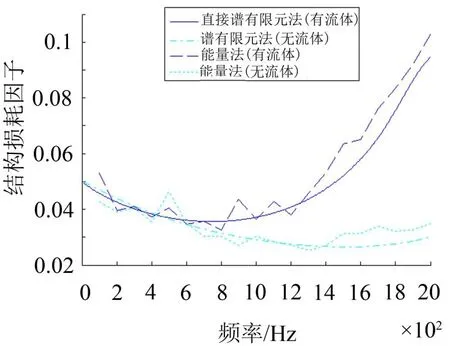
图5 含流体载荷以及不含流体载荷的结构损耗因子对比(直接法)

当基底层较薄或者阻尼层杨氏模量较小的时候，使用直接谱有限元法误差较大，这时需要使用迭代算法。下面对阻尼层杨氏模量E2=108Pa，其他参数同上的自由阻尼板进行仿真计算，其计算结果如图6所示，从中可以看出：当不考虑流体载荷时，谱有限元法和能量法计算结果接近；当考虑流体载荷时，直接谱有限元法计算结果（C曲线）同能量法计算结果（A曲线）差距较大，而迭代谱有限元法计算结果（B曲线）同能量法计算结果接近。

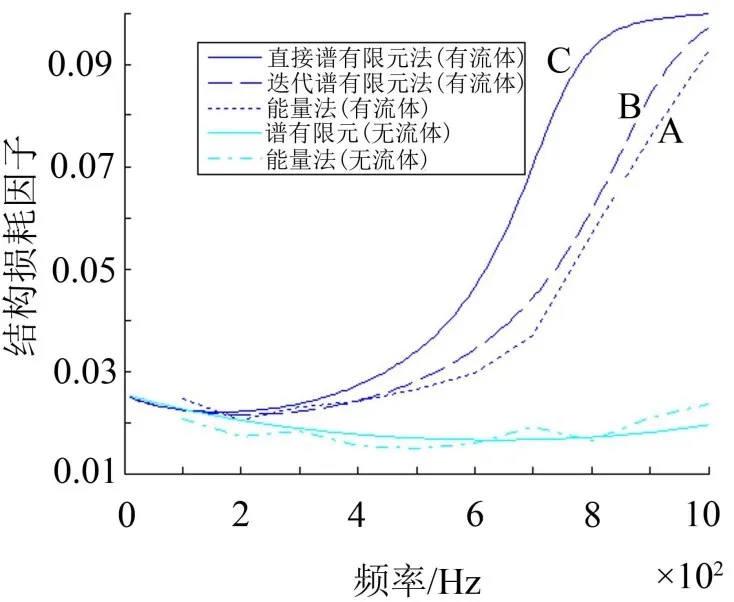
图6 含流体载荷以及不含流体载荷的结构损耗因子对比(迭代法)

从图5和图6还可以看出：无流体的自由阻尼板的结构损耗因子小于有流体的自由阻尼板的结构损耗因子。

以上分析的频率范围为小于第2阶弯曲波产生频率的频段。第2阶弯曲波指的是阻尼层上下表面振动反相，类似于对称兰姆波[15]的波类型。当频率高于上述值时，结构损耗因子随流体载荷的变化很敏感，对于上述方法的分析或者出现不收敛的情况或者收敛到纵波的损耗因子的情形，由于问题的复杂性，本文没有对这种情况进行进一步的研究。

3 辐射损耗因子分析

使用三维弹性理论计算功率转换系数，对辐射损耗因子的特性进行讨论。本节仿真的基本参数与上述谱有限元分析参数相同，其中基底层杨氏模量E2=3×108Pa，板的大小及激励点位置同上一节ANSYS谐响应分析参数。分析时改变上述参数中的某一个，保持其他参数不变。

图7给出了不同阻尼层杨氏模量的功率转换系数随频率的变化曲线，表1给出了所有频率的功率转换系数的平均值，表中可见：从频段平均的角度来看，功率转换系数随着阻尼层杨氏模量的变大而变大。这可以用统计能量分析理论解释如下：阻尼层杨氏模量增大导致自由阻尼板的弯曲刚度增大，从而使得输入功率减小，同时阻尼层杨氏模量的增大会导致声辐射功率的增大[9]，所以功率转换系数相应地增大。

图8给出了不同阻尼层厚度的功率转换系数随频率的变化曲线，从中可以看出：从频段平均的角度来看，功率转换系数随着阻尼层厚度的变大而变小。对这种现象可解释：当阻尼层厚度增大时，阻尼板的弯曲刚度增大，输入功率减小，同时阻尼层的振级落差变大，声辐射功率减小，但是由于阻尼板的弯曲刚度主要由基底决定所以输入功率的减小量比较小，所以总体来说功率转换系数会减小。

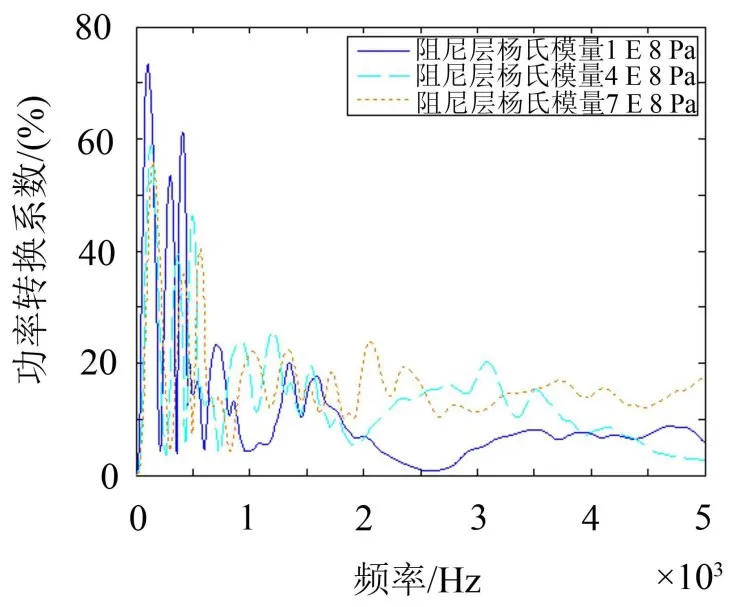
图7 不同阻尼层杨氏模量的功率转换系数

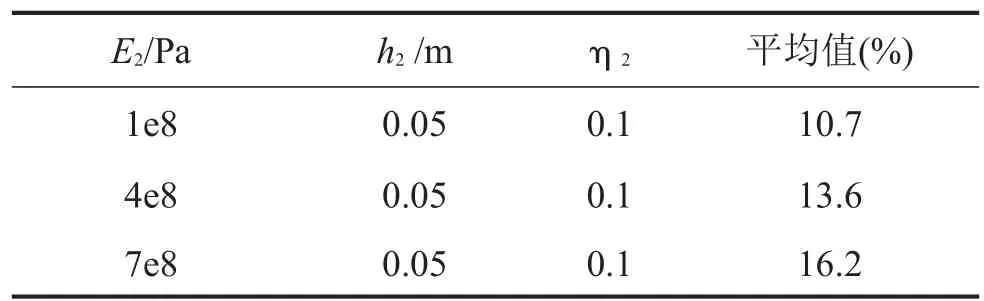
表1 功率转换系数平均值

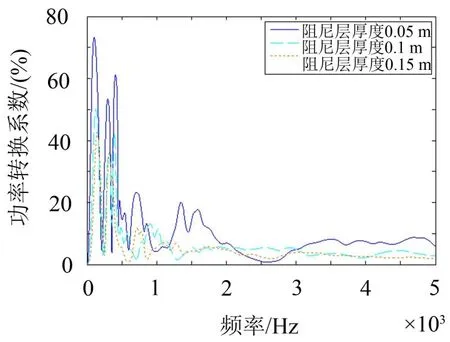
图8 不同阻尼层厚度的功率转换系数

图9给出了不同阻尼层材料损耗因子的功率转换系数随频率的变化曲线，可以看出：从频段平均的角度来看，功率转换系数随着阻尼层材料损耗因子的变大而变小。对这种现象可解释如下：当阻尼层材料损耗因子变大时，由于输入导纳一般变化不会很大[4]，所以输入功率变化也不大，但是振级落差确会因为材料损耗因子的变大而明显变大，这将导致声辐射功率变小，所以功率转换系数会随之变小。

将图7—图9中功率转换系数在低频段和高频段的峰值列在表2中，表中可见：功率转换系数在低频存在较大的峰值，说明在这些峰值频率附近，辐射损耗因子在阻尼损耗因子中所占的比例较大；功率转换系数在高频变化比较平缓，并且其数值较小，所以在高频时辐射损耗因子占阻尼损耗因子的比例较小。

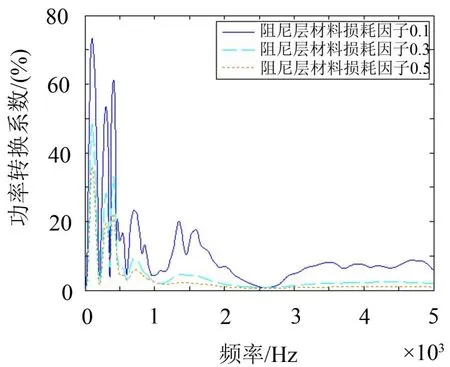
图9 不同阻尼层材料损耗因子的功率转换系数

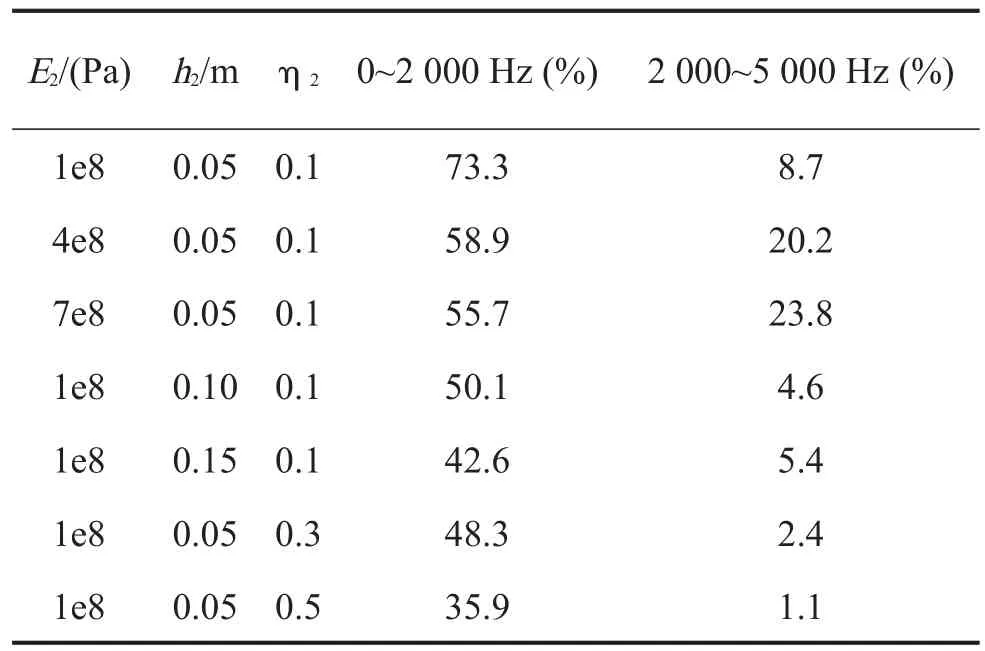
表2 功率转换系数峰值

在仿真中使用的阻尼层材料的材料损耗因子固定为0.1，实际使用的阻尼材料的材料损耗因子一般是随着频率和温度变化的，在低频较大，一般数量级可达到1；阻尼层的厚度为50 mm，实际潜艇上敷设的消声瓦、去耦隔声瓦的声学覆盖层的厚度一般都较厚，有的甚至达到几分米厚；由于以上原因，实际潜艇辐射损耗因子占阻尼损耗因子的比例在某些情况下的某些频率范围内是比较小的，在这些情况下流体载荷主要通过改变结构损耗因子来改变阻尼损耗因子。

4 结语

(1)在低于第2阶弯曲波产生频率的频段范围内，无流体的自由阻尼板的结构损耗因子小于有流体的自由阻尼板的结构损耗因子；

(2)从频段平均的角度来看，功率转换系数随着阻尼层杨氏模量的变大而变大，随阻尼层厚度变大而变小，随阻尼层材料损耗因子变大而变小；

(3)功率转换系数在低频存在较大峰值，在高频变化较为平缓且数值较小；

(4)实际潜艇辐射损耗因子占阻尼损耗因子的比例在某些情况下的某些频率范围内是比较小的，在这些情况下流体载荷主要通过改变结构损耗因子来改变阻尼损耗因子。

[1]孟晓宇，肖国林，陈 虹.国外潜艇声隐身技术现状与发展综述[J].舰船科学技术，2011，11：135-139.

[2]杨龙塾.潜艇声隐身技术[J].现代舰船，2009，11：23-25.

[3]章林柯，何 琳，朱石坚.潜艇主要噪声源识别方法研究[J].噪声与振动控制，2006(04)：7-10.

[4]姜荣俊，何 琳.有源振动噪声控制技术在潜艇中的应用研究[J].噪声与振动控制，2005(02)：1-6.

[5]戴德沛.阻尼减振降噪技术[M].西安交通大学出版社，1986.

[6]Cremer L M.Heckl,et al.Structure-borne sound[M].Springer-Verlag 2005.

[7]Shorter P J.Wave propagation and damping in linear viscoelastic laminates[J].The Journal of Acoustical Society of America,2004,115(5):1917-1925.

[8]Foin O,Berry A.Acoustic radiation from an elastic baffled rectangular plate covered by a decoupling coating and immersed in a heavy acoustic fluid[J].The Journal of the Acoustical Society of America,2000,107(5):2501-2510.

[9]Berry A,Foin O,et al.Three-dimensional elasticity model for a decoupling coating on a rectangular plate immersed in a heavy fluid[J].The Journal of the Acoustical Society of America,2001,109(6):2704-2714.

[10]Laulagnet B,Guyader J L.Sound radiation from finite cylindrical shells,partially covered w ith longitudinal strips of compliant layer[J].Journal of Sound and Vibration,1995,186(5):723-742.

[11]Laulagnet B,Guyader J L.Sound radiation from finite cylindrical coated shells,by means of asymptotic expansion of three-dimensional equations for coating[J].The Journal of the Acoustical Society of America,1994, 96(1):277-286.

[12]Fahy.Sound and structural vibration-radiation, transmission and response[M].Elsevier/Academ ic Press, 1987.

[13]Auto SEA theory and quality assurance manual[M].Australia:1995.

[14]Ungar E E,Kerw in E M.Loss factor of viscoelastic systems in term of energy concept[J].Journal of Acoustical Society of America,1962,34(7):954-957.

[15]杜功焕，朱哲民，龚秀芬.声学基础[M].南京：南京大学出版社，2001.

Influence of Fluid Loading on the Damping Loss Factor of Underwater Unconstrained Damping Plates

YIN Bang-hui,WANG M in-qing

(School of Marine Engineering,Northwestern Polytechnic University,Xi’an 710072,China)

Spectral finite element method is developed for calculating the structural loss factor of an unconstrained damping plate w ith the fluid loading considered.The relationship between the radiation loss factor and power conversion coefficient is analyzed.Then,the structural loss factor of the unconstrained damping plate considering the fluid loading is compared w ith that of the plate w ithout considering the fluid loading.The results are verified by using the energy method.Finally,the power conversion coefficient of the underwater unconstrained damping plate is calculated using threedimensional elastic model.Variation law of the power conversion coefficient w ith the variations of the Young's modulus, thickness and the material loss factor of the damping layer is discussed.The study shows that w ithin the frequency band below the second-order bending wave’s starting frequency,the structure loss factor of the unconstrained damping plate w ithout fluid loading is less than that w ith fluid loading.From the perspective of the frequency average,the power conversion coefficient has large peaks in the low frequency range,and it varies gently and has small values in the highfrequency band.The radiation damping loss factor of the actual submarines under the fluid loading can be changed by changing the structure loss factor.Results of the study may have some reference values for the optimal design of structural damping for submarines.

vibration and wave;fluid loading;unconstraint damping plate;damping loss factor;spectral finite element method;three-dimensional elasticity theory潜艇的声隐身[1—4]对其安全性具有决定作用，在潜艇表面附加一层阻尼材料能有效降低声辐射，提高潜艇隐身性。阻尼损耗因子[5,6]用于描述结构振动时的耗能特性，常用作阻尼处理的评价参数，准确的获取水下自由阻尼板的阻尼损耗因子对于潜艇的抑振降噪具有重要意义。目前对自由阻尼板的阻尼损耗因子的研究大多针对空气中的情况，对于水中的自由阻尼板，由于流体载荷的作用其阻尼损耗因子相对于在空气中将发生较大改变，同时由于阻尼层中传递波的复杂性和流固强耦合的复杂性，现在还没有成熟的理论用于解决上述问题，由此，本文对该问题进行初步研究，旨在对潜艇声学覆盖层的设计和测试评估能提供一定的参考。

1006-1355(2014)04-0071-06

TB53；O328；TH113 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.016

2013-10-20

尹帮辉（1982-），男，四川德阳人，博士生，主要研究方向：振动、噪声及其控制。

王敏庆：男，博士生导师。

Email:mqwang@nwpu.edu.cn