变压器绕组匝间短路故障判断方法探析

张 昕， 陈 鹏， 余 平， 王 贵， 朱 猛

(雅砻江流域水电开发有限公司集控中心，四川 成都 610051)

0 引 言

随着电网容量和规模的扩大，大容量变压器在电力系统中的作用日显突出，电力用户对其安全稳定运行和可靠供电提出了越来越高的要求。差动保护作为电力变压器的主保护，随着科技水平的不断提高相关保护理论得到了不断的发展，在工程实践中也得到了较好的验证。而根据相关资料统计[1]，变压器匝间短路占电力系统中大型变压器故障的50%～60%。匝间短路时的一个典型特点是：短路电流可达额定电流的数十倍，但三相线电流并未显著增大[2]。由于外部短路电流等因数的影响，变压器三相不平衡电流较大，一般情况下，变压器差动保护的整定值都设定较高，不能灵敏反映匝间故障[3]。而传统的反映变压器内部故障的瓦斯保护，无法在故障发生的初期做出快速准确的判断，往往保护动作时变压器内部故障已经发展到相当严重的程度，对变压器的安全稳定运行造成了不利影响。因此，有必要针对变压器匝间短路故障研究出一种更实用快速准确的保护方法。

本文通过在PSCAD/EMTDC中建立电力变压器典型内部匝间短路故障模型，通过Db小波函数研究电流波形数据从而获取准确鉴别内部匝间短路故障的判据和算法。

2 仿真分析

本文采用PSCAD/EMTDC软件进行仿真研究。该软件具有精确的元件模型、方便的数据输入方式及强大的分析功能，主要用来研究电力系统的暂态过程，是系统分析和工程研究的有力工具。该软件包由PSCAD(Power System ComputerAdded Design)和 EMTDC(Electromagnetic Transient Including DC)两部分软件组成，其典型应用是计算电力系统遭受扰动或者参数发生变化时，电信号随时间参数发生变化的规律。特别是软件包含的基于中心几何学建立的UMEC变压器模型，不仅考虑到同相绕组之间的耦合作用，还考虑到不同相绕组间的耦合作用。UMEC模型通过充分利用插值法，以分段的线性U-I曲线来描述铁芯饱和特性，在实时计算时特别是变压器铁芯饱和的情况下可以获得精确的结果。

由于电力系统故障的发生总是会导致相关信号的奇异性产生，因此，分析信号的奇异性可以确定故障发生的时间和原因。而信号突变点(边缘)检测是小波变换应用的一个重要方面。由小波分析理论可知，信号的突变点在小波变换域常对应于小波变换系数模的极值点或过零点，并且信号奇异性的大小同小波变换系数的极值随尺度的变化规律相互对应。

通过综合考虑，仿真所得数据采用MATLAB小波工具包中的Db小波函数进行处理，选用分解尺度为5，以特征较为明显的第3尺度下模极大值作为判断依据，原始信号S=d1+d2+d3+d4+d5+a5,d1至d5分别为第一至第五尺度的高频细节部分，a5为第五尺度下的低频粗糙部分。

图1为仿真变压器匝间短路故障的模型，简要说明如下：

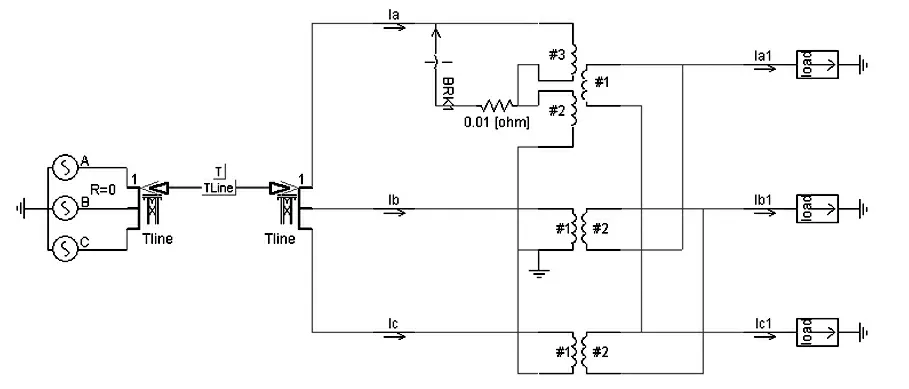
图1 匝间短路故障仿真模型

(1)变压器主要参数为100.0 MVA，YNd11，110/35。采用三个单相变压器进行建模。

(2)由于变压器发生内部匝间故障时电流变化值一般很小，以至传统的继电保护装置无法及时监测到故障信号，考虑到发生小匝数的匝间短路时，所引起的变比变化不明显，因此，设置极端的情况下对保护方案的检验，在匝间短路模型中设定A相发生匝间短路，短路匝数为总匝数的2%。按照参考文献[4]中的思路，一台双绕组变压器发生匝间短路时，可以把短路部分看作第三绕组，这就相当于一台三绕组变压器在第三绕组发生短路，匝间短路模型设计如图1所示。

(3)PSCAD/EMTDC中对原始电流信号每工频周期采样200点，即采样频率为10 kHz。MATLAB中设定在0.2S时发生故障，对一、二次侧采样电流一工频周期时间内的信号数据进行小波分析。

图2、3、4分别为A相发生匝间短路故障后A、B、C三相一、二次侧电流经小波变换后的波形。

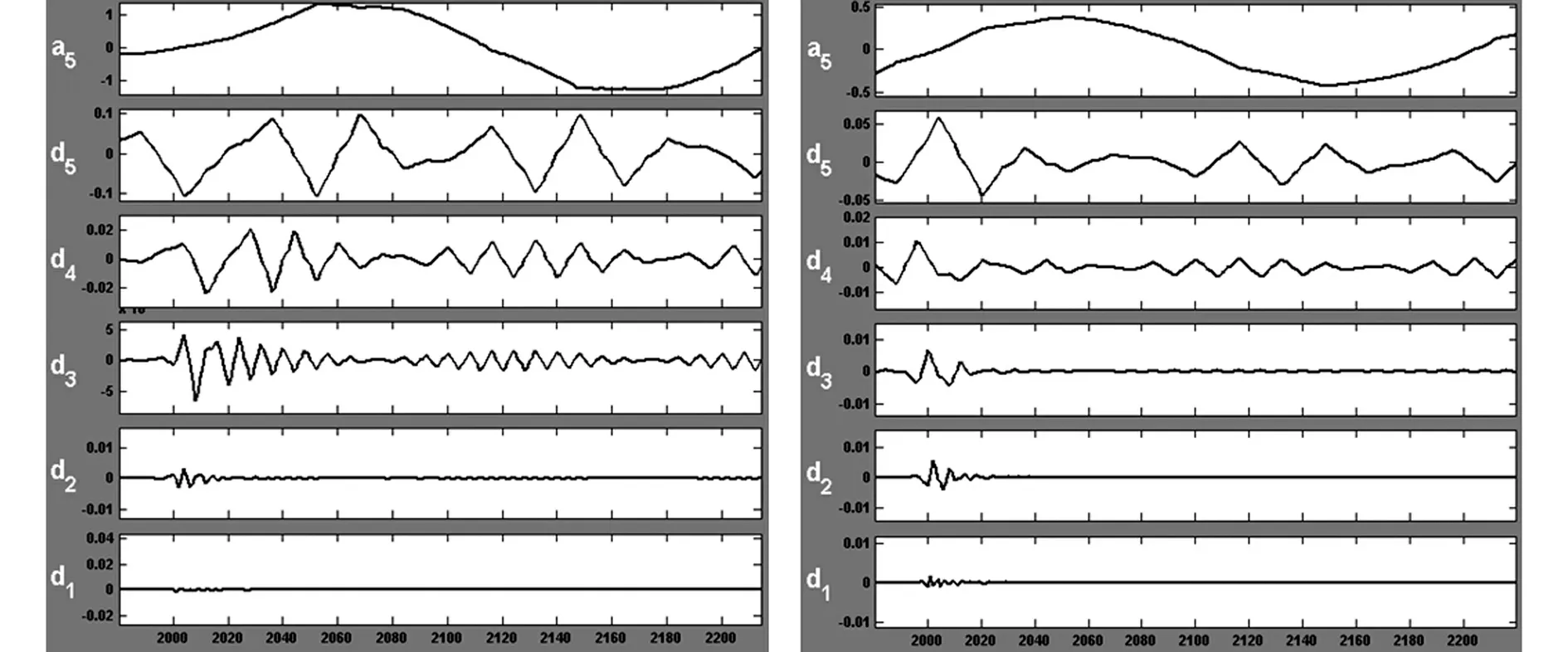
图2 A相匝间短路时，A相一、二次侧电流小波变换

图3 A相匝间短路时，B相一、二次侧电流小波变换

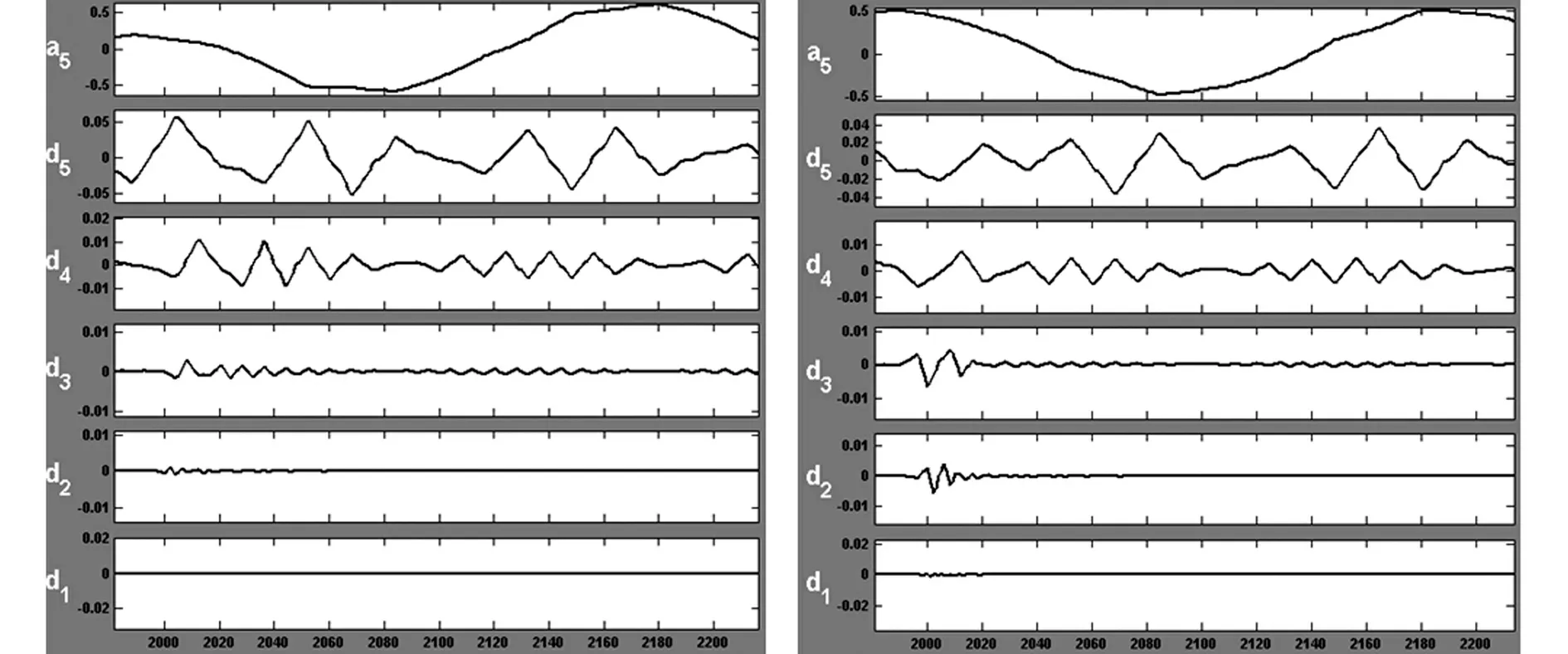
图4 A相匝间短路时，C相一、二次侧电流小波变换

由以上波形可以看出：A相在故障发生后的一工频周期时间范围内的模极大值对应或者接近于于故障发生时刻，并且一、二次侧的模极大值符号相反且绝对值分别为0.0065和0.00679；B相一、二次侧在故障发生后的一工频周期时间范围内的模极大值符号相反且绝对值分别为0.002736和0.0006036；C相一、二次侧在故障发生后的一工频周期时间范围内的模极大值符号相反且绝对值分别为0.00287和0.00638。

上述仿真研究是直接对一、二次侧电流进行信号采样分析，但实际工程运用中往往是通过电流互感器将信号进行转化并接入保护回路进行数据分析，通常我们会假定电流互感器是线性传变信号的，但实际运用中电流互感器存在着磁饱和问题。对于电压等级较低的电网，一般只要有所注意，保护装置适应电流互感器的饱和并无太大困难。但在较高等级电压的电网中，考虑到故障电流初始值中含有的直流分量，若要满足快速保护对电流互感器过渡过程饱和时的要求就要复杂困难得多。

实际上，由于电流互感器只能在故障发生一定时间之后才会饱和，这一时间段至少有四分之一个周期[5]。而仿真数据结果表明，在一个工频周期内，所需要进行分析判断的模极大值部分均在1/4周期内，因此可以认为分析数据基本不受电流互感器饱和的影响。

3 保护方法设计

上述仿真研究结果表明：对于匝间短路故障情况，故障发生相一二次侧对应的模极大值点的幅值其正负性是相反的，若采用适当的门槛值，将模极大值过小的点归结为零，则可以认为非故障相两侧的模极大值点总是有存在为零的情况。

对应于本文的研究内容，可设定门槛值K为0.003，绝对值小于该门槛值的模极大值均设定为零。表1是将仿真所得到的数据处理后的结果。可以看出当发生故障时，故障相一、二次侧电流信号模极大值电流幅值符号相反，而正常相的乘积则为零。因此，不但可以依据其乘积的符号对故障的发生做出判断并且可以进一步判断出故障所在相。

表1 匝间短路故障时小波变换模极大值点电流幅值

综上所述，所设计的判据如下：

假设变压器差动保护回路分别在三相各自独立判断，I1(t)、I2(t)分别为采样区间内某相一、二次侧电流小波变换模极大值点的幅值，设K为门槛值且K=0.003，若

|I1(t)|

(1)

|I2(t)|

(2)

有：

S=I1(t)×I2(t)

(3)

若数据运算后S<0，保护回路发出信号“1”；若小波变换后某相一次或二次侧电流幅值的绝对值低于门槛值K则S=0，保护回路发出信号“0”。将三相各自一二次侧电流数据计算后发出的“0”和“1”进行“或”运算，若结果为“1”则保护装置发出变压器跳闸信号，并根据各相反馈回的“0”“1”信号判断故障具体发生在哪一相。若“或”运算结果为“0”，保护装置则继续对采样信号进行分析判断。

4 结 语

考虑到工程应用环境的复杂，在实际应用中还需不断完善判据。若门槛值K选取过高，有可能使得轻微故障情况下仅凭判断S的数值并不能做到足够准确的判断，甚至会导致拒动情况发生。同时在对电流信号的分析处理过程中也存在着电流信号波动干扰导致的误判可能，因此，该判据的具体设定还需要在实际工作中不断总结归纳以取得更合理的设置。总体来说，该方法计算简单，所用数据量较少，能在匝间短路故障发生初期就做出快速准确判断，具有一定的可行性和实用性。

参考文献：

[1] 尹项根. 电力系统继电保护原理与应用[M]. 武汉:华中科技大学出版社, 2001.

[2] 李秀国. 变压器匝间短路故障的分析与处理[J]. 山东电力技术, 2009(6): 28-29.

[3] 王维俭. 发电机变压器继电保护应用[M]. 北京:中国电力出版社, 2005.

[4] 王维俭,侯炳蕴.大型机组继电保护理论基础[M].北京:水利电力出版社，1982.

[5] KEZUNOVIC, M, KOJOVIC, L. Experimental Evaluation of EMTP-based Current Transformer Models for Protective Relay Transient Study. IEEE Transactions on, 1994, 9(1): 405-413.