具有收获率和非线性死亡率的脉冲Nicholoson’s blowflies模型正周期解

姚晓洁

(柳州师范高等专科学校数学与计算机科学系，柳州 545004)

近年来，关于连续型Hematopoiesis模型的研究引起了许多学者的广泛关注，其研究成果大部分集中对时滞Hematopoiesis模型的周期解或概周期解的存在性或不存在性、唯一性、全局吸引性或指数稳定性[1-6]. 最近，文献[7]讨论了下面一类具有非线性依赖密度死亡率的Nicholson’s blowflies模型

N′(t)=-a(t)+b(t)e-N(t)+

c(t)N(t-(t))e-γ(t)N(t-(t))

(1)

的正周期解的存在性问题，这里a,b,c,,γC(,(0,∞))都是ω-周期函数.利用重合度理论，获得了方程(1)正周期解存在的充分条件.然而，笔者还未见具有非线性依赖密度死亡率和非线性收获率的脉冲Nicholson’s blowflies模型周期解的相关报道，因此，本文将研究如下一类具有非线性收获率和非线性依赖密度死亡率的脉冲Nicholson’s blowflies模型

(2)

的正周期解，这里a(t),b(t),ci(t),i(t),γi(t),δ(t)C(,(0,∞)),HC(2,[0,∞))，n>0为正整数.

模型(2)的初始条件为

(3)

(A2){dk}是实数列且满足dk>0,k=1,2,….

(A3)a(t),b(t),ci(t),i(t),δ(t),H(t,·)和都是关于t的ω-周期函数，ω>0为常数，i=1,2,…,n.

显然，模型(1)是模型(2)的特殊情形.本文通过利用重合度理论和不等式分析技巧，获得了方程(2)正周期解的充分条件，从而推广和改进了文献[7]的相关结果.最后列举一个例子表明本文所得结果的可行性.

1 准备知识

(i)N(t)在(0,t1]与(tk,tk+1](k=1,2,…)上绝对连续；

(iii)N(t)满足系统(2),

则称N(t)为模型(2)在[-,∞)上的解.

考虑如下无脉冲Nicholson’s blowflies模型

(4)

引理1 假设条件(A1)～(A3)满足，则

(i)如果y(t)是系统(4)在[-,∞)上的解，则是系统(2)在[-,∞)上的解；

(ii)如果N(t)是系统(2)在[-,∞)上的解，则是系统(4)在[-,∞)上的解.

引理1的证明类似文献[8]引理2.5的证明，这里省略.

根据引理1可知，讨论模型(2)的正ω-周期解的存在性，只需考虑方程(4)正ω-周期解的存在性.为了获得方程(4)正周期解，先引入重合度理论.

(iii)deg{JQN,Ω∩KerL,0}≠0，

2 主要结果

证明作变换y(t)=ex(t)， 则方程(4)变为

(5)

N:X→Z,Nx=Δ(x,t).

考虑Lx=Nx,(0,1)，即

x′(t)=Δ(x,t).

(6)

设x(t)是式(6)对于某个(0,1)的ω-周期解，则存在ξ,η[0,ω]，使得

(7)

由式(6)和式(7)可得

(8)

(9)

由式(8)可得

结合条件mb-/M(a++H+)>1，得

(10)

由条件mb-/M(a++H+)>1得

(11)

(12)

QN(-H0)>0,QN(H0)<0.

(13)

事实上，如果QN(-H0)≤0，即

于是有

如果QN(H0)≥0，即

deg{QN,Ω∩KerL,0}=deg{-x,Ω∩KerL,0}≠0.

如果dk=1(k=1,2,…)，则此时模型(2)变成无脉冲系统

N′(t)=-a(t)+b(t)e-N(t)+

H(t,N(t-δ(t)).

(14)

于是由定理1立即可得：

推论1 如果a(t),b(t),ci(t),i(t),γi(t),H(t,·)(i=1,2,…,n)都是关于t的ω-周期函数，ω>0为常数，则当时，模型(14)至少存在一个正ω-周期解.

推论2 如果a(t),b(t),c(t),(t),γ(t)都是ω-周期函数，ω>0为常数，则当b-/a+>1,ea-γ->c+时，模型(1)至少存在一个正ω-周期解.

3 应用举例

例1 考虑如下具有非线性收获率和非线性依赖死亡率的脉冲Nicholoson’s blowflies模型

(15)

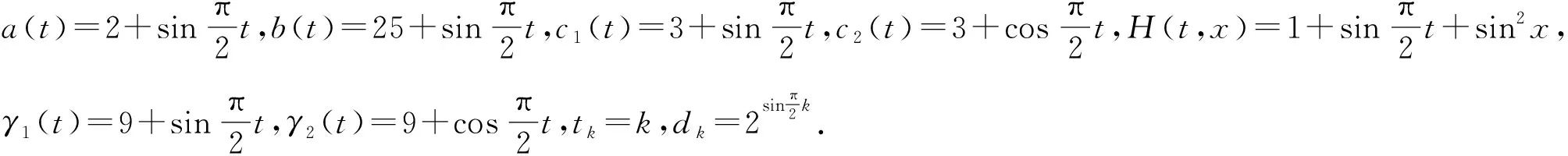
从而根据定理1知，方程(15)至少存在一个正4-周期解.

参考文献：

[1] Liu G,Yan J,Zhang F. Existence and global attractivity of unique positive periodic solution for a model of hematopoiesis[J].Journal of Mathematical Analysis and Applications, 2007,34:157-171.

[2] Wang X,Li Z. Dynamics for a class of general hematopoiesis model with periodic coefficients[J].Applied Mathematics and Computation, 2007,186(1): 460-468.

[3] Wang X, Zhang H. A new approach to the existence, nonexistence and uniqueness of positive almost periodic solution for a model of hematopoiesis[J]. Nonlinear Analysis-Real World Applications,2010,11:60-66.

[4] Yang X. Existence and global attractivity of unique positive almost periodic solution for a model of hematopoiesis[J].Applied Mathematics-A Journal of Chinese Universities,2010, 25(1):25-34.

[5] Zhang K, Li L. Almost periodic solution in a model of Hematopoiesis with impulses[J]. Mathematical Theory and Applications，2013,33(2):20-28.

[6] Zhang H, Yang M, Wang L. Existence and exponential convergence of the positive almost periodic solution for a model of hematopoiesis[J]. Applied Mathematics Letters, 2013,26:38-42.

[7] Wang W. Positive periodic solutions of delayed Nicholson’s blowflies models with a nonlinear density-density mortality term[J].Applied Mathematical Modelling, 2012,36:4708-4713.

[8] Zhang H, Li Y, Jing B, et al. Global stability of almost periodic solution of multispecies mutualism system with delays and impulsive effects[J]. Applied Mathematics and Compuation,2014,232:1138-1150.

[9] Gaines R E, Mawhin J. Coincide degree and nonlinear differential equations[M]. Berlin:Springer-Verlag,1997.