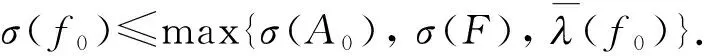一类亚纯函数系数线性微分方程亚纯解的增长性
2014-08-28蔡琳琳陈宗煊
蔡琳琳, 陈宗煊
(华南师范大学数学科学学院,广州 510631)
1 引言与结果
本文假定读者熟悉亚纯函数的值分布的基本理论和标准记号[1-2]. 另外, 用和(1/f)分别表示亚纯函数f(z)的零点、不同零点和极点收敛指数, degP表示多项式P(z)的次数,σ(f)和σ2(f)分别表示f(z)的增长级和超级[3],σ2(f)被定义为
1982年,Bank和Laine[4]首先利用值分布理论研究了二阶齐次线性微分方程解的复振荡性质. 随后,Gao等[5-7]对整函数系数线性微分方程进行了一系列的研究. 2002年,曹春雷和陈宗煊[8]讨论了一类没有优势系数的高阶线性微分方程的解,得到
定理A 假设A0,A1,…,Ak-1(k≥2)是不全恒等于零的有限级整函数,若对每个Aj(j为整数, 0≤j≤k-1), 如果Aj≢0, 有(Aj)<σ(Aj), 且对Ai≢0,Aj≢0 (i≠j), 有σ(Ai/Aj)=max{σ(Ai),σ(Aj)},那么,微分方程
f(k)+Ak-1f(k-1)+…+A0f=0
(1)
的任一超越解f满足σ(f)=∞. 进一步, 如果按A0,A1,…,Ak-1的顺序, 第一个不恒等于零的系数为Aj,则方程(1)最多出现次数不超过j-1的多项式解,其余解均为无穷级;若A0≢0,则方程(1)的任一非零解均为无穷级.

f(k)+Ak-1f(k-1)+…+A0f=F,
(2)
有



在文献[8]的基础上, 本文将方程的整函数系数推广到亚纯函数系数, 运用与文献[8]不同的方法, 证明了下面的定理.
定理1 假设Aj(z)=Bj(z)ePj(z)(j=0,1,…,k-1),Aj不全恒等于零,Bj(z)是亚纯函数,Pj(z)=aj,mjzmj+…+aj,0为非常数多项式,aj,q(q=0,1,…,mj)为复常数,aj,mj≠0,且满足
(1)σ(Bj) (2)当i≠j时, deg(Pi-Pj)=max{mi,mj}≤σ(A0); (3)当mj=σ(A0)且argaj,mj=arga0,m0时, |aj,mj|<|a0,m0|, 那么微分方程(1)的任一非零亚纯解f都满足σ(f)=∞.特别地,如果f(z)的极点重数一致有界,那么σ2(f)=σ(A0). 定理2 假设Aj(z)=Bj(z)ePj(z)(j=0,1,…,k-1),Aj满足定理1的条件,F≢0为有限级亚纯函数. 那么方程(2)至多有一个有限级例外亚纯解,其他所有亚纯解f都满足 如果方程(2)有有限级亚纯解f0, 那么f0满足 引理1[9]假设f是超越亚纯函数且σ(f)=σ<∞,H={(k1,j1),(k2,j2),…,(kq,jq)}是一个不同整数对的有限集, 且满足ki>ji≥0 (i=1,2,…,q), 假设ε>0 是一任意给定常数, 那么 (3) exp{-rσ+ε}≤|f(z)|≤exp{rσ+ε}. 引理3[7]若非齐次线性微分方程(2)满足Aj(j=1,…,k-1),F≢0为有限级亚纯函数,f为方程(2)的无穷级亚纯解, 则 注1 在引理4中,当α=2,i=0时,有 (j=1,2,…,k). 引理5[11]假设g(z)是无穷级整函数且σ2(g)=σ,而ν(r)是g(z)的中心指标,那么 引理6[7]假设g:(0,+∞)→,h:(0,+∞)→是单调增函数,满足g(r)≤h(r)除去一个对数测度有限的集合E外,则对任意α>1,存在r0>0,使得对所有的r>r0,g(r)≤h(αr)成立. 引理7[12]假设g(z)为亚纯函数,σ(g)=β<+∞,那么对任意给定的ε>0,存在一个线测度和对数测度都为有穷的集合E2⊂(1,+∞),使得当 第1步:证明方程(1)的所有非零解都为无穷级. (4) 由于Pj(z)=aj,mjzmj+…+aj,0(aj,mj≠0), 令aj,mj=|aj,mj|eiφj,z=reiθ, 则 Pj(z)=|aj,mj|rmjei(φj+mjθ)(1+o(1)), 且 |exp{Pj(z)}|= exp{|aj,mj|rmjcos(φj+mjθ)}(1+o(1)). (5) 我们不妨设A0,A1,…,Ak-1全不恒等于零(A0,A1,…,Ak-1不全恒等于零类似可证).下面将j=0,1,…,k-1 分为三大类,记为 J1={j: 0 J2={j: 0 J3={j: 0 由于f为超越解, 则由方程(1)可知, (6) exp{-rσ(Bj)+ε}≤|Bj(z)|≤exp{rσ(Bj)+ε}. (7) |Bj(z)ePj(z)|≤exp{rσ(Bj)+ε}exp{|aj,mj|rmj× (8) |B0(z)eP0(z)|≥exp{-rσ(B0)+ε+ |a0,m0|rm0cos(m0θ*+φ0)}(1+o(1))= exp{|a0,m0|rm0cos(m0θ*+φ0)}(1+o(1)). (9) 及 |Bj(z)ePj(z)|≤exp{rσ(Bj)+ε+ |aj,mj|rm0cos(m0θ*+φj)}(1+o(1))=O(1). (10) |Bj(z)ePj(z)|≤exp{rσ(Bj)+ε+ |aj,mj|rm0cos(m0θ*+φ0)}(1+o(1))≤ (11) 将式(4)、(8)、(10)和式(11)代入式(6)可知,在射线argz=θ*上, 有 O(rkσ). (12) |a0,m0|rm0cos(m0θ*+φ0)}O(rkσ)+ exp{-|a0,m0|rm0cos(m0θ*+φ0)}O(rkσ)+ 这是矛盾的. 所以σ(f)=∞. (ii)再证方程(1)无有理函数解.若f(z)为方程(1)的有理函数解,类似(i)的方法,同理可证与式(6)是矛盾的.故方程(1)的每个非零解都为超越解. 综上所述,方程(1)的任一非零解都具有无穷级. 第2步:若f(z)的极点重数一致有界,下证σ2(f)=σ(A0). 先证σ2(f)≤σ(A0).由方程(1)可知,f(z)的极点仅可能发生在A0,A1,…,Ak-1的极点处,则有 又由于f(z)是方程(1)的超越亚纯解且极点重数一致有界, 故有 及 σ(g)=σ(f)=∞,(d)=σ(d)<∞. 方程(1)可写为 (13) 由数学归纳法证明得到 其中Cj j1…jn为常数且j+j1+2j2+…+njn=n,则 (14) 将式(14)代入式(13)得 (15) 其中 (16) |Aj(z)|≤exp{rσ(Aj)+ε}≤exp{rσ(A0)+ε}. (17) (18) 由式(16)~(18)知,对所有的i=0,1,…,k-1,有 |Bi(z)|≤|Ai(z)|+(|Ai+1(z)|+…+ |Ak-1(z)|+1)O(rM)≤O(rM)exp{rσ(A0)+ε}, (19) 其中M为某正数. 由σ(g)=∞知g(z)是超越整函数,由Wiman-Valiron[13]理论, 在圆周|z|=r上满足|g(z)|=M(r,g)的z点处,除去一对数测度有穷的集合E5⊂(1,+∞)外,当z→∞时,有 (20) 其中vg(r)是g(z)的中心指标. 即 |vg(r)|≤O(rM+1)exp{rσ(A0)+ε}. (21) 由于ε是任意的,则由引理5及式(21)可知σ2(g)≤σ(A0),即 σ2(f)=σ2(g)≤σ(A0). (22) exp{|a0,m0|rm0cos(m0θ*+φ0)}(1+o(1))≤ B(T(2r,f))j+1+B(T(2r,f))k+1≤ kB(T(2r,f))k+1× 所以 exp{|a0,m0|rm0cos(m0θ*+φ0)}(1+o(1))≤ 即 kB(T(2r,f))k+1. (23) 综上所述,σ2(f)=σ(A0). 假设f1和f2是方程(2)的有限级亚纯解(f1≢f2),则f1-f2是方程(2)对应的齐次方程(1)的亚纯解且σ(f1-f2)<∞.这与定理1矛盾.所以方程(2)至多出现一个有限级亚纯解. 现假设方程f为方程(2)的无穷级亚纯解,那么由引理3,有 设f0是方程的有限级亚纯解,方程(2)可改写为 (24) 由式(24),若z0为f0的α(α>k)阶零点,而A0,A1,…,Ak-1在点z0处解析,则F在点z0处至少有α-k阶零点,从而 于是有 (25) 由σ(f0)<∞及对数导数引理得到 (26) 由式(25)和式(26)可得 参考文献: [1] Hayman W K. Meromorphic functions[M]. London: Oxford, 1964. [2] 杨乐. 值分布论及其新研究[M]. 北京: 科学出版社, 1982. [3] 仪洪勋, 杨重骏. 亚纯函数唯一性理论[M]. 北京:科学出版社, 1995. [4] Bank S B, Laine I. On the oscillation theory off″+Af=0 whereAis enire[J]. Transactions of the American Mathematical Society, 1982, 273: 351-363. [5] Gao S A. On the complex oscillation of solutions of non-homogeneous linear differential equations with polynomial coefficients[J]. Comment Mathematici Universitatis Sancti Pauli, 1989, 38: 11-20. [6] Chen Z X, Gao S A. Entire solutions of differential equations with finite order transcengdental coefficients[J]. Acta Mathematica Sinica, 1997, 13: 453-464. [7] Gao S A, Chen Z X, Chen T W. The complex oscillation theory of linear differential equations (in Chinese)[M]. Wuhan: Huazhong University of Science & Technology Press, 1998. [8] 曹春雷, 陈宗煊. 一类整函数系数线性微分方程解的增长性和零点[J]. 应用数学学报, 2002, 25(1): 123-131. Cao C L, Chen Z X. On the orders and zeros of the solutions of certain linear differential equations with entire coefficients[J]. Acta Mathematicae Applicatae Sinica, 2002, 25(1): 123-131. [9] Gundersen G G. Estimates for the logarithmic derivatives of a meromorphic function, plus similar estimates[J]. London Mathematical Society, 1988, 37(2): 88-104. [10] 陈宗煊, 孙光镐. 一类二阶微分方程的解和小函数的关系[J]. 数学年刊:A 辑, 2006, 27(4): 431-442. Chen Z X, SHON Kwang-Ho. The relation between solutions of a class of second order differential equation with functions of small growth[J]. Chinese Annals of Mathematics:Series A, 2006, 27(4): 431-442. [11] Chen Z X. On the hyper-order of solutions of some second-order linear differential equations[J]. Acta Mathematica Sinica:English Series, 2002, 18(1): 79-88. [12] 陈宗煊. 二阶亚纯系数微分方程亚纯解的零点[J]. 数学物理学报,1996,16(3): 276-283. Chen Z X.The zeros of meromorphic solutions of second-order differential equations with meromorphic coefficients[J]. Acta Mathematica Scientia, 1996,16(3): 276-283. [13] 何育赞,肖修治. 代数体函数与常微分方程[M].北京:科学出版社,1988.
2 引理






3 定理1的证明














4 定理2的证明