高含钢率钢骨混凝土柱的滞回数值分析
2014-08-27赵宪忠
秦 浩 赵宪忠
(同济大学建筑工程系,上海 200092)
1 引 言
钢骨混凝土(简称SRC)结构与传统的混凝土结构和钢结构相比具有更好的承载性能、防火性能和抗震性能等优点,因此被广泛地应用于高层、超高层和复杂建筑结构中[1]。
为了较为准确、全面地把握钢骨混凝土构件的受力性能,采用有限元数值分析方法对其进行力学行为的模拟,是一种行之有效的方法[2-4]。在有限元数值模拟过程中,材料本构的输入是其中最关键的步骤,决定了其数值结果的准确性。采用传统的材料本构(即混凝土采用《混凝土结构设计规范》中的应力应变曲线[5],钢材直接采用单调拉伸的试验数据),有限元模拟结果与试验相比会明显偏于保守[6]。其原因有三:①钢骨混凝土构件中钢筋和钢骨对混凝土具有一定约束作用,造成混凝土强度和延性的提高[2,3,7];②在反复荷载作用下,混凝土出现损伤,混凝土的损伤会造成混凝土刚度的降低[7-9];③在反复荷载作用下,钢材出现循环硬化现象,钢材循环骨架曲线强度高于单调加载曲线的钢材强度[10,11]。
本文通过ABAQUS对文献[6]中的钢骨混凝土柱滞回试验进行有限元模拟,在进行材料本构输入时,考虑了混凝土的约束、损伤以及钢材的硬化引起的材料性能变化,建立了适用于滞回加载条件下的有限元分析模型,并与试验进行对比,验证了其模拟的准确性。同时分析探讨了材料本构的性能变化对高含钢率钢骨混凝土柱滞回性能的影响。
2 有限元模型
2.1 试件参数
高含钢率钢骨混凝土柱滞回性能数值模拟的原型模型采用文献[6]中的所列的试验试件,试件的混凝土强度为C50,钢材为Q235,截面形式如图1所示,截面参数如表1所示。

图1 试件截面尺寸(单位:mm)Fig.1 Section of the SRC members (Unit: mm)
表1试件参数
Table1Parametersofthespecimens

编号hss/mmbf/mmtw/mmtf/mm轴压力/kN试验轴压力系数Z10-65R2241008163 9900.65Z15-65R22410016203 1000.65Z15-80R22410016204 3500.80Z20-65R22410025254 6000.65
试验中将SRC组合柱设计为一压弯悬臂柱,其加载力学模型如图2(a)所示。为方便同实验机加载头的连接,在柱顶处设置了销铰装置,试验装置示意如图2(b)所示。
对构件首先施加竖向作用力至预定值(表1中的轴压力)并保持大小不变,再施加等幅升幅的水平位移,每级均循环三次。施加位移的回载控制点如下:±0.5△y、±1△y、±2△y、±4△y、±6△y、±8△y,直至构件破坏或者水平荷载下降至峰值荷载的30%以下。
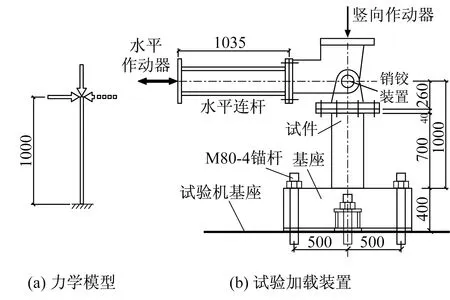
图2 试件加载原理及装置Fig.2 Testing model and arrangement
2.2 有限元模型的建立
本文研究的钢骨混凝土柱根据材料不同可以分为钢骨部分、钢筋部分和混凝土部分。混凝土部分根据所受约束的不同,又分为钢筋约束混凝土部分(简称半约束混凝土)和钢骨约束混凝土部分(简称高约束混凝土)。Mander[7]提出了钢筋混凝土约束区域的划分,Mirza[2],Chen和Lin[3]则对钢骨约束混凝土进行区域划分,其划分区域如图3所示。

图3 SRC柱截面区域划分Fig.3 Regions for composite sections
为应用方便,Ellobody[4]将图3中的工字形SRC柱中的弧形区域划分简化为直线形,本文同样针对于十字形截面钢骨混凝土柱,也将其截面约束区域进行直线形简化,如图4所示。
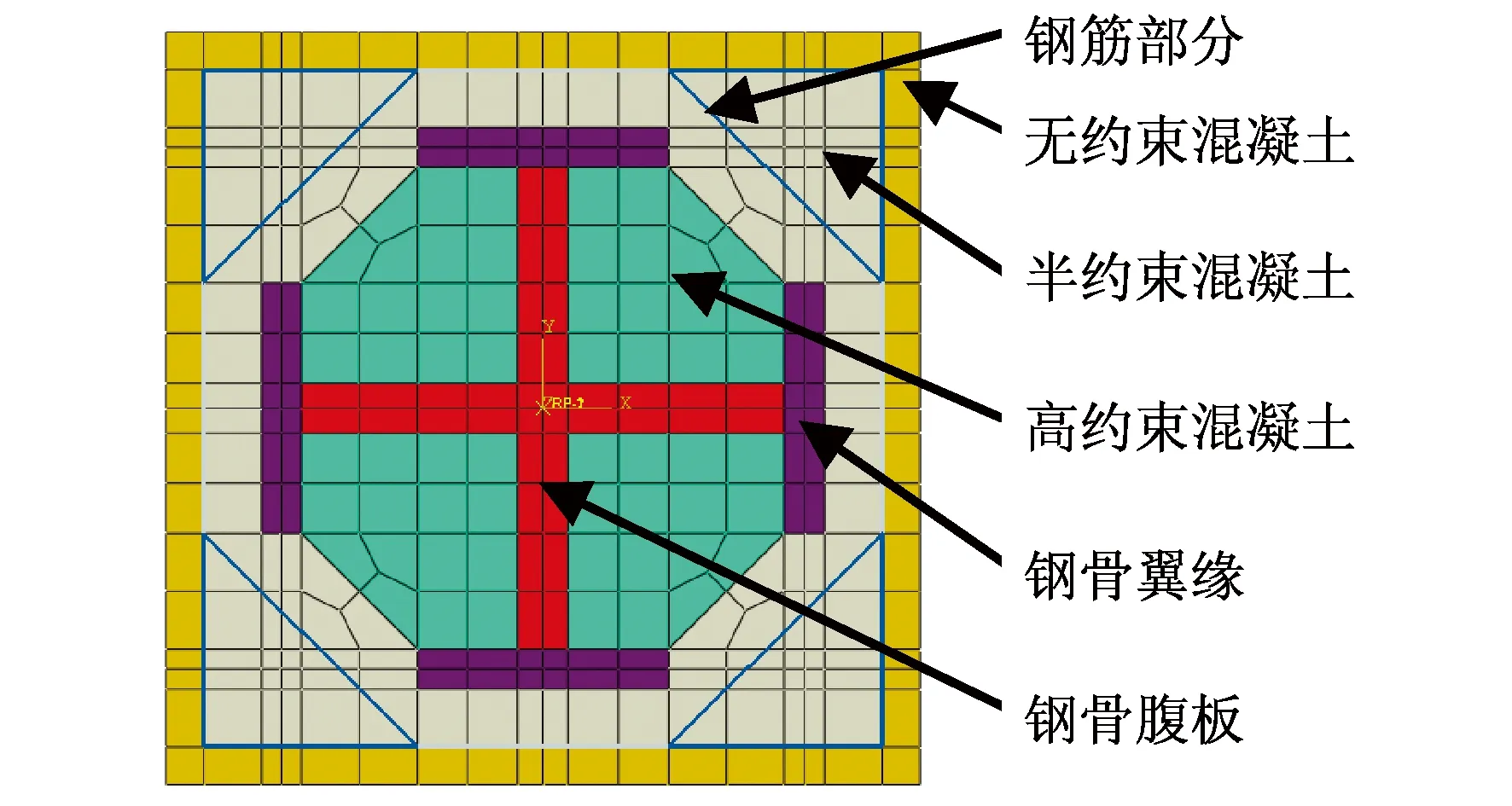
图4 SRC柱截面区域简化Fig.4 Regions simplified for composite sections

图5 SRC柱整体模型Fig.5 The whole FEA model of SRC columns
有限元整体模型(图5)按实际尺寸建模,钢骨、混凝土部分采用C3D8R单元(8节点6面体减缩积分单元);纵向钢筋和箍筋采用T3D2桁架单元。钢筋部分则通过ABAQUS中的embed功能嵌入到混凝土中。由于试件的钢骨翼缘设置了足够的抗剪栓钉,加载过程中未出现明显的粘结滑移现象,因此在有限元模拟过程中假定钢骨和混凝土之间无滑移。
2.3 混凝土材料本构的定义
无约束混凝土区域、半约束混凝土区域和高约束混凝土区域的应力应变曲线如图6所示。

图6 混凝土本构关系曲线Fig.6 Stress-strain curves for concrete
(1) 无约束混凝土区域选用《混凝土结构设计规范》附录C中的混凝土本构关系曲线[5]。fc′为混凝土圆柱体强度标准值。
(2) 半约束混凝土则采用Mander钢筋约束混凝土本构模型,其应力应变σ-ε曲线公式如下:
(1a)
(1b)
(1c)
(1d)
(1e)

εcp——半约束混凝土峰值应变;
fcp——半约束混凝土峰值应力;
kp1——半约束混凝土强度提高系数,取值方法参见Mander约束混凝土研究文献[7],本文试件取值见表2;
kp2——半约束混凝土应变提高系数。
(3) 高约束混凝土与半约束混凝土本构曲线形式相似。
(2a)
(2b)
(2c)
(2d)
(2e)
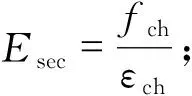
εch——高约束混凝土峰值应变;
fch——高约束混凝土峰值应力;
kh1——高约束混凝土强度提高系数,依据Chen和Lin的研究[3],本文试件取值见表2;
kh2——高约束混凝土应变提高系数。
表2约束混凝土强度和应变提高系数
Table2Coefficientofstrengthandstrainforconfinedconcrete

试件fc'/MPa半约束混凝土kp1kp2高约束混凝土kh1kh2Z10-65R38.21.282.401.604.00Z15-65R45.31.242.202.006.00Z15-80R38.71.282.402.006.00Z20-65R39.01.282.402.006.00
(4) 混凝土损伤的定义[12]。本文混凝土采用ABAQUS中的混凝土损伤塑性模型,该模型在模拟混凝土的受力行为方面具有其他有限元软件无可比拟的优越性。通过定义损伤因子反映混凝土在循环加载过程中的刚度退化,如图7所示。
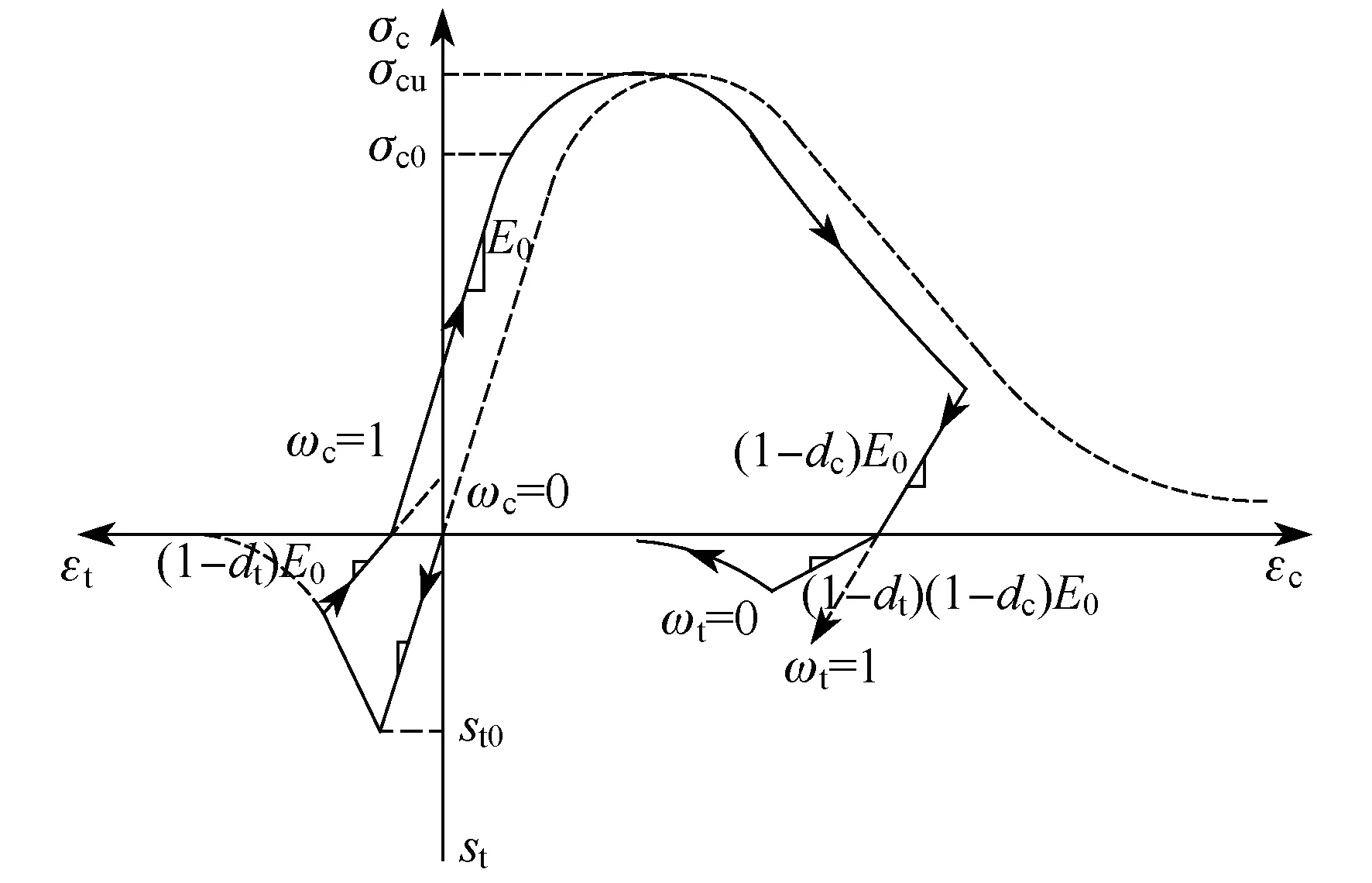
图7 ABAQUS混凝土损伤塑性模型
Fig.7 ABAQUS concrete damage plastic model
注:σc,σt分别为混凝土受压和受拉应变;σc0,σt0分别为混凝土弹性最大受压和受拉应变;σcu为混凝土最大受压应变;dc,dt分别为混凝土受压和受拉损伤因子;ωt为混凝土受拉刚度恢复因子(ABAQUS默认裂缝产生后受拉刚度为0,即ωt=0);ωc为混凝土受压刚度恢复因子(ABAQUS默认裂缝闭合后受压刚度完全恢复,即ωc=0);E0为混凝土初始弹性模量。
混凝土损伤因子,采用经典损伤理论法计算[13],其定义如下:
(3)

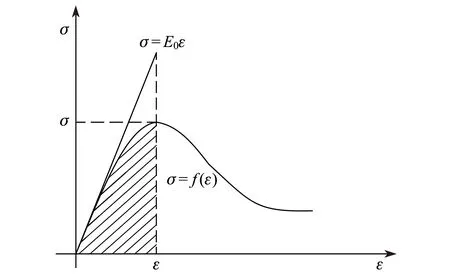
图8 混凝土损伤的定义Fig.8 Definition of concrete damage
2.4 钢材本构的定义
钢材在单调和循环荷载下的受力表现形式是不同的,钢材单调加载的本构响应呈现弹性—屈服点效应—应变硬化典型变形特性,如图9(a)所示,而循环塑性本构响应最显著的特点便是屈服点效应不存在了,下一循环对前一循环的应力或应变幅值及循环次数的依赖关系显得格外突出。在循环加载过程中钢材出现硬化,如图9(b)所示[10]。因此对于钢材不同的受力行为应选用不同的本构模型。

图9 钢材的本构Fig.9 Constitutive relationships of structural steel
高含钢率SRC柱的力学性能更接近于钢柱[14],其钢骨材料本构的定义对SRC柱力学性能的影响起至关重要的作用。

(4)

图10 钢材材性试验数据Fig.10 Test data of structural steel property
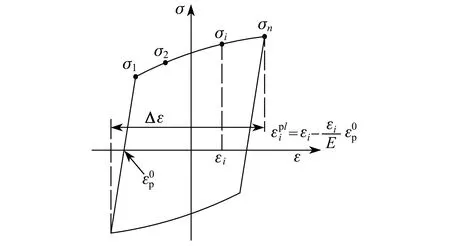
图11 ABAQUS钢材全周期滞回模型Fig.11 ABAQUS stabilized cycle of structural steel property
2.5 试件的有限元与试验结果对比
图12为所有试件的有限元与试验结果的对比。由对比可知,采用本文提出的混凝土和钢材本构,所有试件的有限元计算结果与试验结果均吻合良好。

图12 所有试件的有限元与试验结果对比Fig.12 Comparison between FEA result and test result for all specimens
3 材料本构对计算结果的影响
本节选取文献[6]中Z15-65R构件进行有限元分析计算,考察材料本构对有限元计算结果的影响。
3.1 混凝土约束对结果的影响
图13为有限元模拟中混凝土不考虑约束和钢材采用全周期滞回本构的计算结果与试验的对比。由对比可知,在SRC柱有限元模拟中不考虑混凝土约束的影响,有限元计算结果与试验相比明显偏低,并且在无法表现出SRC柱强度退化的规律。

图13 混凝土不考虑约束的有限元计算结果与试验结果对比Fig.13 Comparison between FEA result without confinement of concrete and test result
3.2 混凝土损伤对结果的影响
图14为有限元模拟中混凝土考虑约束但不考虑损伤和钢材采用全周期滞回本构的计算结果与试验的对比。由对比可知,在SRC柱有限元模拟中考虑混凝土的约束后,其峰值强度与试验结果的峰值强度趋于相近,同时由于不考虑混凝土损伤的影响,有限元计算结果滞回环无法表现出试验中SRC柱强度退化的规律。
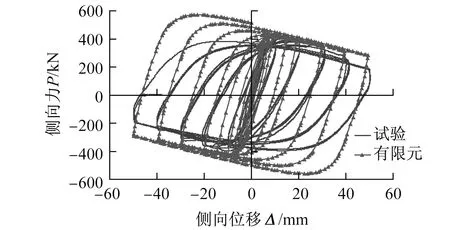
图14 混凝土不考虑损伤的有限元计算结果与试验结果对比Fig.14 Comparison between FEA result without damage of concrete and test result
3.3 钢材单调和滞回本构对结果的影响
图15为有限元模拟中混凝土考虑约束和损伤,钢材为单调本构的计算结果与试验的对比。由对比可知,在SRC柱中考虑混凝土的约束和损伤后,滞回环的刚度和强度退化规律与试验接近,但由于钢材在循环荷载作用下出现材料硬化,单调本构的强度低于钢材滞回本构的强度,因此有限元计算结果低于试验结果。
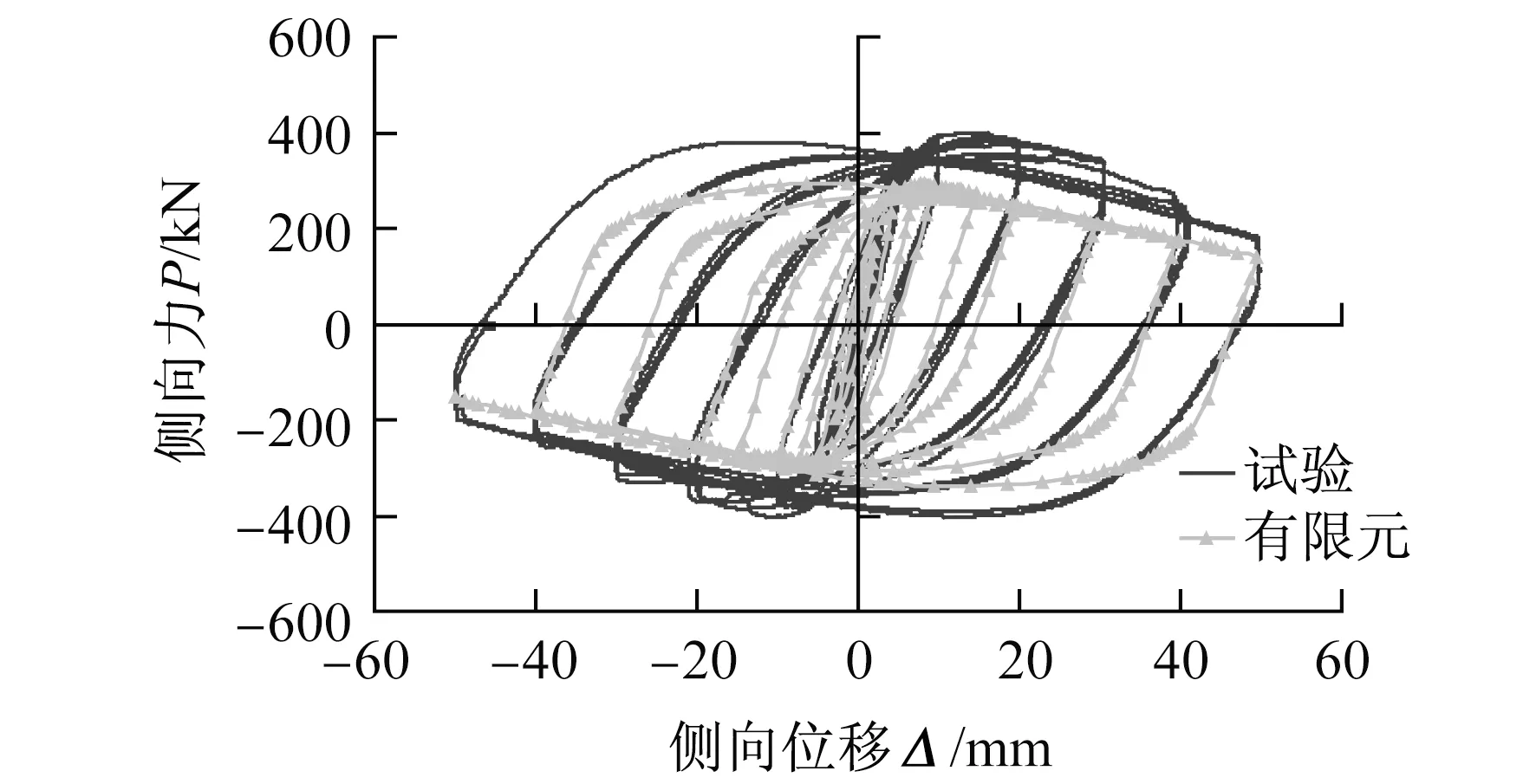
图15 钢材为单调本构的有限元计算结果与试验结果对比Fig.15 Comparison between FEA result with monotonic property of steel and test result

图16 钢材为滞回本构的计算结果与试验结果对比Fig.16 Comparison between FEA result with cyclic property of steel and test result
图16为有限元模拟中混凝土考虑约束和损伤,钢材采用全周期滞回本构的计算结果与试验的对比。由对比可知,在SRC柱中考虑混凝土的约束和损伤,钢材选用全周期滞回本构之后,有限元计算结果和滞回规律与试验相比,均十分接近。
由以上对比分析可知,采用本文提出的考虑约束和损伤的混凝土本构以及钢材滞回本构,在高含钢率SRC柱有限元数值计算中可以达到较好模拟结果。
4 结 论
在钢骨混凝土柱的有限元模拟中,钢骨和混凝土的材料本构对其计算结果有至关重要的影响。若忽略其中混凝土所受的约束和损伤,以及钢材在反复荷载作用下循环硬化的特性,则有限元的计算结果与试验结果将会存在较大差距。
本文在进行钢骨混凝土柱的有限元模拟中,材料本构的输入考虑了这些因素的影响,经过同文献[6]中滞回试验结果的对比,验证了本文滞回材料本构的适用性,为相关试件的研究和参数分析提供了依据。
[ 1 ] 赵鸿铁.钢与混凝土组合结构[M].北京:科学出版社,2001.
Zhao Hongtie. Steel and concrete composite structure [M]. Beijing: Science Press, 2001. (in Chinese)
[ 2 ] Mirza S A, Skrabek B W. Statistical analysis of slender composite beam-column strength[J]. Journal of Structural Engineering, 1992, 118(5): 1312-1332.
[ 3 ] Chen C C, Lin N J. Analytical model for predicting axial capacity and behavior of concrete encased steel composite stub columns[J]. Journal of Constructional Steel Research, 2006, 62(5): 424-433.
[ 4 ] Ellobody E, Young B. Numerical simulation of concrete encased steel composite columns[J]. Journal of Constructional Steel Research, 2011, 67(2): 211-222.
[ 5 ] 中华人民共和国住房和城乡建设部. GB 50010—2010 混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.
Ministry of Construction of the People’s Republic of China. GB 50010—2010 Code for design of concrete structures[S]. Beijing: China Architecture and Building Press, 2010. (in Chinese)
[ 6 ] 王海生.高含钢率钢骨混凝土柱滞回性能研究[D].上海:同济大学,2008.
Wang Haisheng. Reaserch on hysteretic behavior of steel reinforced concrete columns with high ratio of core steel [D]. Shanghai: Tongji University, 2008. (in Chinese)
[ 7 ] Mander J B, Priestley M J N, Park R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826.
[ 8 ] Lubliner J, Oliver J, Oller S, et al. A plastic-damage model for concrete[J]. International Journal of Solids and Structures, 1989, 25(3): 299-326.
[ 9 ] Lee J, Fenves G L. Plastic-damage model for cyclic loading of concrete structures[J]. Journal of Engineering Mechanics, 1998, 124(8): 892-900.
[10] 董永涛,张耀春.建筑用钢循环塑性本构模型[J].哈尔滨建筑工程学院学报,1993(5):106-112.
Dong Yongtao, Zhang Yaochun. Cyclic plastic constitutive model for structural steel [J]. Journal of Harbin University of Civil Engineering and Architecture, 1993(5): 106-112. (in Chinese)
[11] 孙伟.钢结构常用钢材滞回性能试验研究[D].上海:同济大学,2010.
Sun Wei. Experiment study on hysteretic behavior of structural steel [D]. Shanghai: Tongji University, 2010. (in Chinese)
[12] Abaqus analysis user′s manual v6.10[M]. ABAQUS Inc, 2010.
[13] 秦浩,赵宪忠.ABAQUS混凝土损伤因子取值方法研究[J].结构工程师,2013(6):27-32.
Qin Hao, Zhao Xianzhong. Study on ABAQUS damage parameter in concrete damaged plasticity model[J]. Structural Engineers, 2013(6): 27-32. (in Chinese)
[14] 中华人民共和国国家发展和改革委员会. YB 9082—2006 钢骨混凝土结构技术规程[S].北京,2006.
National Development and Reform Commission. YB 9082—2006 Technical specification of steel-reinforced concrete structures[S]. Beijing, 2006. (in Chinese)
