正交各向异性功能梯度夹层板的自由振动分析
2014-08-26李华东朱锡梅志远张颖军
李华东,朱锡,梅志远,张颖军
(海军工程大学舰船工程系,湖北武汉430033)
功能梯度材料(functionally graded materials,FGM)[1-2]由2种或2种以上材料按不同组分复合,其材料性能在某一方向上连续梯度变化,消除了明显的界面和性能突变,在工程结构中的应用越来越广泛。
目前,在单一功能梯度结构和功能梯度夹层结构动态性能的研究方面,采用高阶剪切变形理论和高阶层合板理论,Pradyumna等[3-4]分别给出了功能梯度曲板和具有功能梯度芯材的夹层梁自由振动问题的解,而Neves等[5]则采用考虑厚度方向变形的高阶剪切变形理论,对功能梯度板和功能梯度夹层板的自由振动和屈曲性能进行研究。而采用Ritz法,Zhao等[6-7]分别对功能梯度板和功能梯度夹层板的自由振动进行了分析。
通过对现有文献的分析可以看出,目前对于如下形式的功能梯度夹层结构:表层为厚度较薄、弹性模量较高的正交各向异性材料,芯材为厚度较大、弹性模量较低的FGM振动特性研究还未见有报道。本文基于Reissner假设,对表层为正交各向异性复合材料,芯材为FGM的功能梯度夹层矩形板的自由振动问题进行了研究,FGM芯材的泊松比保持恒定,而弹性模量在厚度上呈任意函数Eg(z)变化。
1 位移与内力分布假设
如图1所示,本文研究的功能梯度夹层板的表层较硬(厚度为t),而芯材较软(厚度为h),因而在本文中,采用Reissner理论的下列假设[8]:1)表层厚度较薄,因而假设应力沿其厚度均匀分布,即处于薄膜应力状态。2)芯材模量较低,忽略其平行于xy平面的应力,即σx=σy=τxy=0。3)只考虑夹层板的反对称变形模式,即在芯材和表层中,εz=0,σz=0。

图1 功能梯度夹层矩形板Fig.1 FGM sandwich rectangular plate
1.1 芯材的应力和位移场
在本文中,上表层为z轴负方向的面,下表层为z轴正方向的面,则由假设2及芯材在x、y方向上的平衡方程[9]:

得出
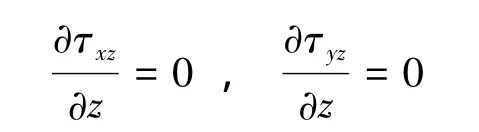
可以看出剪应力在梯度芯材上是均匀分布的,而根据剪切应力的边界条件,在夹层板的上下表面处:

由于上下表层较薄,所以可以假设剪切应力在表层中呈线性分布,得到剪切应力τxz、τyz在厚度上方向上的分布如图2[10]所示。
假设Qx、Qy为夹层板中的总横向剪力,则得到芯材中的剪切应力[8]为
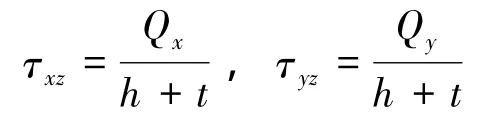
根据胡克定律,芯材相应的剪应力变为

式中:u、v和w为芯材中各点在x、y和z轴方向的位移;Gg(z)为芯材在xz和yz平面内的剪切模量,其表达式为
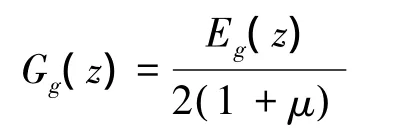
将式(1)对z积分,得出

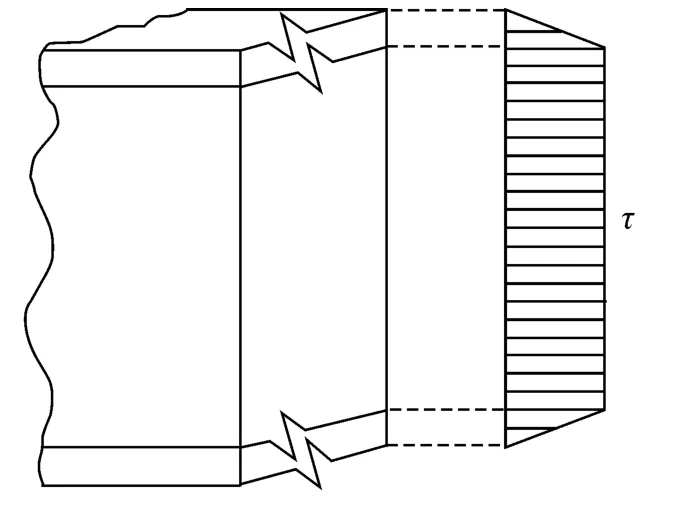
图2 厚度方向横向剪应力分布假设Fig.2 The variation assumption of transverse shear stress through the thickness
1.2 表层位移场假设
假设u+、v+为下表层中面各点在x、y轴方向的位移,u-、v-为上表层中面各点在x、y轴方向的位移,根据假设 1 得[11]:

以上位移的偏导数

在平面应力问题中,物理方程如下:

式中:

由式(3)可以得出表层的应力-应变关系为

式中:
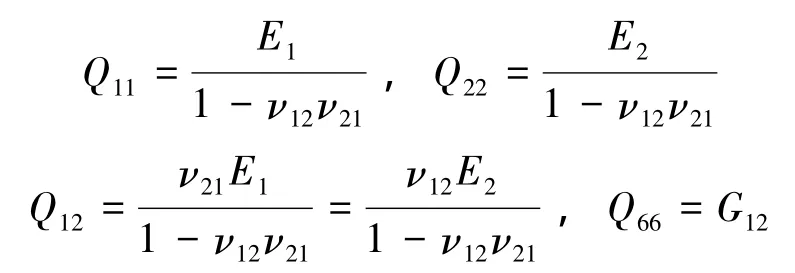
根据:
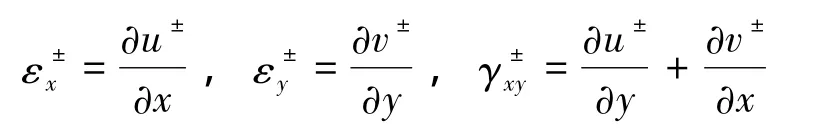
则

1.3 板的内力表达式
夹层板总弯矩Mx、Mx和总扭矩Mxy=Myx为[8]

将式(2)、(4)代入上式得

式中:

2 运动方程及求解
2.1 运动方程
对于功能梯度夹层板而言,其仍满足单层板的如下运动平衡方程:
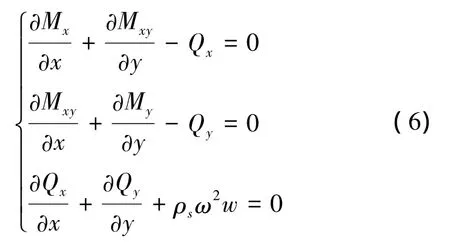
式中:ω为圆频率,ρs为功能梯度夹层结构的面密度,其计算式如下

式中:ρf为夹层结构上下表层的体积密度,ρc(z)为FGM芯材密度的分布函数。
将式(5)代入平衡方程(6),可得

2.2 方程的求解
首先,根据“四边简支”边界条件:

设

由运动方程(6),得
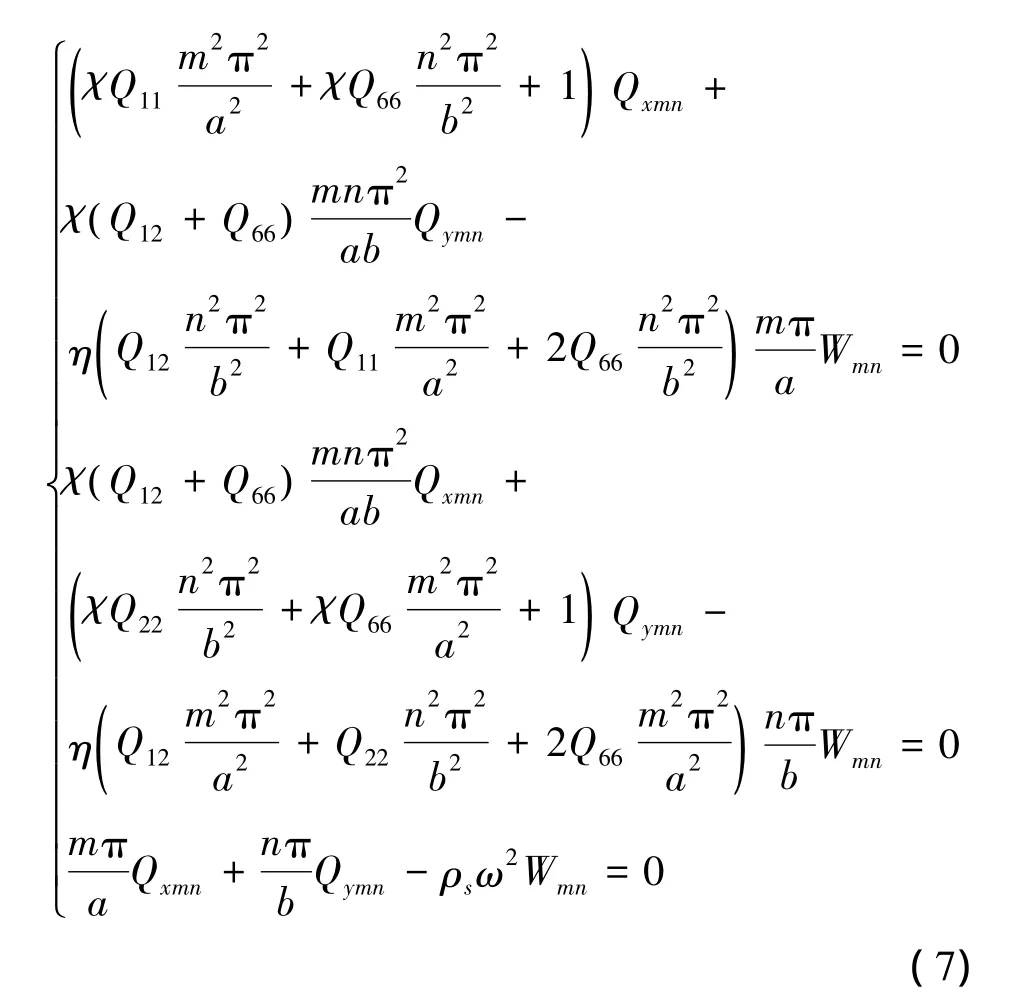
方程(7)的前2个式子可以简写为如下线性方程组的形式

式中:

则

式中:
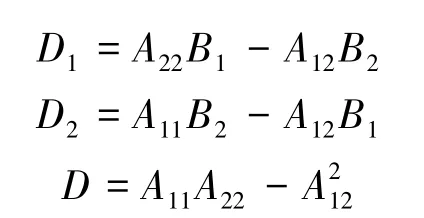
将式(8)代入平衡方程(7)的第3个式子,得

因为Wmn≠0,则

则,功能梯度夹芯板固有频率的计算式为

3 功能梯度夹层板固有频率计算
3.1 弹性模量呈线性分布的FG夹层板固有频率
夹层板总厚度为50 mm,其上下表层与芯材的厚度分别为5 mm与40 mm,面内尺寸:a=b=1 000 mm。表层为正交异性材料,其材料工程弹性常数为:Ex=140 GPa,Ey=8.6 GPa,Gxy=5 GPa,νxy=0.35,ρf=1.2×10-6kg/mm3。芯材为功能梯度材料,其弹性模量分布遵循:
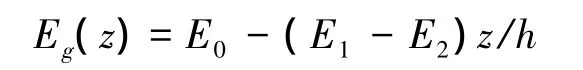
式中,E0=Eg(0)=55 MPa,而E1=100 MPa、E2=10 MPa分别为芯材上下表面处的弹性模量,芯材泊松比 μ=0.45,ρc=0.8×10-6kg/mm3。
为验证本文方法计算结果的正确性,采用有限元仿真软件ABAQUS对本问题进行计算。在厚度方向上利用20层等厚度的均质各向同性材料对FGM芯材进行模拟,单元类型为三维实体线性缩减单元C3D8R,而表层采用skin技术,单元类型为二维线性缩减壳单元S4R。为与有限元仿真结果一致,将角频率转化为频率f,其计算式如下:

功能梯度矩形夹层板各阶固有频率的有限元仿真结果和本文解的对比如表1所示,从中可以看出,本文解与有限元仿真结果相近,最大误差为2.1%,说明本文方法具有较高的正确性和精确度。
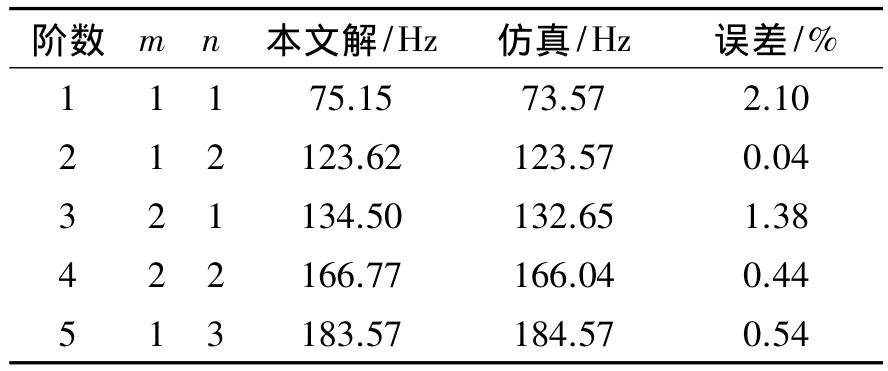
表1 矩形夹层板固有频率f的对比Table 1 Comparison of natural frequencies f of rectangular sandwich plates
3.2 弹性模量呈幂律分布的FG夹层板固有频率
计算FGM芯材的弹性模量呈如下幂律分布时,3.1节中的FG夹层矩形板的固有频率。芯材弹性模量的分布遵循以下函数[12-13]:
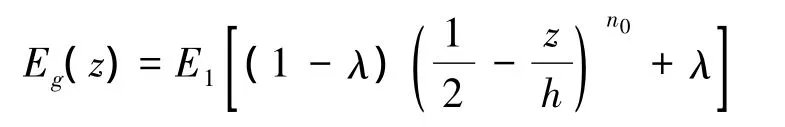
式中:E1为芯材上表面处的弹性模量,λ为芯材下表面与上表面处的弹性模量的比值,n0为组分材料体积分数指数。
对参数λ和n0、跨厚比δ及面内尺寸比κ对表层为正交各向异性材料的功能梯度夹层矩形板固有频率的影响进行分析,在本节中,比值δ和κ的定义式如下

同时,定义无量固有频率的计算式如下[13]

式中,ρf和Ey为表层的密度和弹性模量。
3.2.1 材料参数对FG夹层板固有频率的影响
如表2所示,给出了当FGM芯材的密度在厚度方向上保持恒定,且a=b=1 000 mm时,λ和n0对正交各向异性功能梯度夹层矩形板的一阶固有频率的影响。从表中可以看出:1)对于不同取值的n0,FG夹层矩形板的一阶无量纲固有频率均随λ的增大而增大;2)当λ<1时,FG夹层板的一阶无量纲固有频率随着n0的增大而降低,反之则相反。
表2 FG夹层板的一阶无量纲频率(ρc为常数)Table 2 The non-dimensional fundamental frequencyof FG sandwich plates(ρcis constant)

表2 FG夹层板的一阶无量纲频率(ρc为常数)Table 2 The non-dimensional fundamental frequencyof FG sandwich plates(ρcis constant)
images/BZ_193_397_1612_1105_1671.png0.1 4.17 3.53 2.9 0.2 4.33 3.87 3.42 1 5 5 5 2 5.46 5.66 5.86 5 6.24 6.67 7.08 10 6.95 7.49 7.98
假设芯材的密度遵循如下与弹性模量一致的分布函数:

式中,ρt=0.8×10-6kg/mm3。
表3 FG夹层板的一阶无量纲频率(ρc=ρc(z))Table 3 The non-dimensional fundamental frequency ω-of FG sandwich plates(ρc= ρc(z))

表3 FG夹层板的一阶无量纲频率(ρc=ρc(z))Table 3 The non-dimensional fundamental frequency ω-of FG sandwich plates(ρc= ρc(z))
images/BZ_193_397_2567_1105_2626.png0.1 4.72 4.3 3.86 0.2 4.83 4.6 4.37 1 5 5 5 2 4.9 4.85 4.81 5 4.45 4.26 4.13 10 3.9 3.63 3.45
如表3所示,当FGM芯材密度ρc遵循式(9)变化时,参数λ和n0对固有频率的影响与密度ρc保持恒定时不同,可以看出:1)当λ<1时,随λ的增大而增大,反之则相反;2)对于λ<1和λ>1时,随着n0的增大而降低。可以看出,当FGM芯材的密度在厚度方向上变化时,材料参数对结构一阶固有频率的影响与密度保持恒定时不同。
3.2.2 跨厚比δ对FG夹层板固有频率的影响
研究FGM芯材的密度保持恒定且a=b时,FG夹层矩形板的跨厚比δ对不同λ和n0的正交各向异性功能梯度夹层矩形板固有频率的影响。如图3所示,分别给出了功能梯度夹层矩形板一阶无量纲固有频率随跨厚比δ=a/(h+2t)的变化规律,从图3中可以看出,对正交各向异性功能梯度夹层板而言,无量纲频率随跨厚比δ的增大而升高。

图3 无量纲固有频率随跨厚比δ的变化规律Fig.3 The non-dimensional fundamental frequencyversus side-to-thickness ratio δ

图4 无量纲固有频率随纵横比κ的变化规律Fig.4 The non-dimensional fundamental frequencyversus aspect ratio κ
3.2.3 面内纵横比κ对FG夹层板固有频率的影响
研究当b=1 000 mm且FGM芯材的密度在厚度方向上保持恒定时,面内纵横比κ=a/b对不同λ和n0的正交各向异性FG夹层矩形板无量纲频率的影响,由图4可以看出,对正交各向异性功能梯度夹层板而言,随面内纵横比κ的增大而降低。
4 结论
基于Reissner假设,本文对四边简支的功能梯度夹层矩形板的自由振动问题进行了研究,得到了表层为正交各向异性材料的FG夹层矩形板固有频率的理论解,并详细探讨了材料属性分布参数λ和n0、结构跨厚比δ及面内纵横比κ对芯材弹性模量在厚度方向上呈幂律分布的FG夹层板固有频率的影响。通过本文的分析可以看出:
1)对于表层为正交各向异性材料的FG夹层矩形板而言,当芯材的密度在厚度方向上保持恒定时,其一阶无量纲固有频率均随λ的增大而增大;
2)在跨厚比δ和纵横比κ已定时,当λ<1时,一阶无量纲固有频率随着n0的增大而降低,反之则相反。
3)在λ已定时,无量纲频率随跨厚比δ=a/(h+2t)的增大而升高,随面内纵横比κ=a/b的增大而降低。
4)而当其芯材密度在厚度方向上变化时,FGM芯材的材料属性分布参数λ和n0对功能梯度夹层板固有频率的影响与芯材密度保持恒定时不同,在实际应用时,需要针对Ec(z)和ρc(z)特定的分布函数进行分析。
[1]CHI S H,CHUNG Y L.Mechanical behavior of functionally graded material plates under transverse load—Part I:Analysis[J].International Journal of Solids and Structures,2006,43:3657-3674.
[2]GILHOOLRY D F,BATRA R C,XIAO J R,et al.Analysis of thick functionally graded plates by using higher-order shear and normal deformable plate theory and MLPG method with radial basis functions[J].Composite Structures,2007,80:539-552.
[3]PRADYUMNA S,BANDYOPADHYAY J N.Free vibration analysis of functionally graded curved panels using a higherorder finite element formulation[J].Journal of Sound and Vibration,2008,318:176-192.
[4]RAHMANI O,KHALILI S M R,MALEKZADEH K,et al.Free vibration analysis of sandwich structures with a flexible functionally graded syntactic core[J].Composite Structures,2009,91:229-235.
[5]NEVES A M A,FERREIRA A J M,CARRERA E,et al.Static free vibration and buckling analysis of isotropic and sandwich functionally graded plates using a quasi-3D higherorder shear deformation theory and a meshless technique[J].Composites:Part B,2012,89:148-155.
[6]ZHAO X,LEE Y Y,LIEW K M.Free vibration analysis of functionally graded plates using the element-free kp-Ritz method[J].Journal of Sound and Vibration,2009,319:918-939.
[7]LI Q,LU V P,KOU K P.Three-dimensional vibration analysis of functionally graded material sandwich plates[J].Journal of Sound and Vibration,2008,311:498-515.
[8]中国科学院北京力学研究所.夹层板壳的弯曲稳定和振动[M].北京:科学出版社,1977:93-100.Institute of Mechanics,Chinese Academy of Sciences.The bending stability and vibration of sandwich plates and shells[M].Beijing:Science Press,1977:93-100.
[9]徐芝纶.弹性理论[M].北京:高等教育出版社,2006:41-45.XU Zhilun.Elasticity mechanics[M].Beijing:Higher Education Press,2006:41-45.
[10]李华东,朱锡,梅志远,等.分布载荷作用下简支功能梯度夹层板的弯曲分析[J].复合材料学报,2012,29(2):213-217.LI Huadong,ZHU Xi,MEI Zhiyuan,et al.Bending analysis of the simply supported functionally graded sandwich plate distributed load[J].Acta Materiae Compositae Sinica,2012,29(2):213-217.
[11]李华东,朱锡,梅志远,等.轴向压力下功能梯度夹层圆柱曲板的屈曲分析[J].华中科技大学学报:自然科学版,2012,40(11):72-76.LI Huadong,ZHU Xi,MEI Zhiyuan,et al.Buckling analysis of functionally graded sandwich cylindrical panels under axial compression[J].J Huazhong Univ of Sci& Tech:Natural Science Edition,2012,40(11):72-76.
[12]BAYAT M,SAHARI B B,SALEEM M,et al.Bending analysis of a functionally graded rotating disk based on the first order shear deformation theory[J].Applied Mathematical Modelling,2009,33:4215-4230.
[13]CHAKRABORTY A,GOPALAKROSHNAN S,REDDY J N.A new beam finite element for the analysis of functionally graded materials[J].International Journal of Mechanical Sciences,2003,45:519-539.
