孟加拉湾MADE KYUN河三角洲海底斜坡稳定性数值分析*1

周其坤，孙永福，胡光海，袁顺新，丁继胜，张海泉

(1.国家海洋局 第一海洋研究所，山东 青岛 266061；2.中国石油天然气管道工程有限公司，河北 廊坊 065000)

孟加拉湾MADEKYUN河三角洲海底斜坡稳定性数值分析*1

周其坤1，孙永福1，胡光海1，袁顺新2，丁继胜1，张海泉1

(1.国家海洋局 第一海洋研究所，山东 青岛 266061；2.中国石油天然气管道工程有限公司，河北 廊坊 065000)

对MADE KYUN河三角洲海底斜坡所在区域地形地貌、地层岩性等进行阐述分析，结合调查资料确定了斜坡坡体组成与特征：该斜坡坡体主要为淤泥、淤泥质黏土，厚度6～9 m。基于GEO-SLOPE软件的SLOPE/W模块计算斜坡稳定性安全系数并确定最危险滑动面，利用BING软件的Herschel-Bulkley模型、双线型模型对最危险滑动面的滑移距离进行模拟预测。数值分析结果表明：在考虑孔隙水压力的情况下，4种计算方法得到的稳定性系数均有所下降，M-P法计算得到的斜坡稳定性安全系数为0.606，处于不稳定状态；2种模型计算得到的滑移距离分别为207和213 m，峰值滑移速率分别为7.80和9.33 m/s，会对较大范围的海底管道等海底设施造成破坏性影响。

孟加拉湾；GEO-SLOPE；海底稳定性；BING；滑移距离

海底滑坡作为近海三角洲以及大陆坡范围内常见的一种地质过程，已经成为对海洋工程构筑物甚至人类安全威胁最大的地质灾害之一[1]。相对于陆上滑坡，海底滑坡发生的地形坡度一般较小，即使在坡度很小的情况下(小于1°)，滑坡形成的碎屑流可凭借“滑水”(Hydroplaning)效应[2]，高速运动至数千米甚至数百千米远。在边坡的稳定性分析方法中，极限平衡法目前已发展成为一套具有完整理论体系的、成熟的分析方法[3-4]。该方法于1916年由彼得森提出，经过改进发展至今，不同的条间力假定形成了不同的分析方法[5-10]。基于极限平衡理论开发的GEO-SLOPE软件应用广泛[11-12]，且在许多大型工程中均有应用，可靠性得到验证，效果良好[13]。海底滑坡滑移距离的预测计算，能够对防灾减灾起到指导性作用。BING是由Imran开发的一套利用有限差分方法来计算海底滑坡的软件[14]，缪成章利用该软件对Isfjorden和Bear Island Fans地区的海底滑坡碎屑流的滑移距离进行计算[15]，探讨了影响海底滑坡滑移距离以及流滑速度的因素，计算结果与实测结果比较接近。

研究区位于孟加拉湾MADE KYUN河三角洲某海底管道路由区内，其稳定性对油气管道的安全生产有着重要的影响；关于此区域的研究甚少。为此，我们利用数值模拟的方式对研究区的海底斜坡稳定性进行分析，并对潜在危险滑动面的滑移距离进行计算。

1 研究区背景

研究区(图1)位于缅甸皎漂市马德岛东部海域，是MADE KYUN河与孟加拉湾海域交汇处。每年雨季MADE KYUN河携带泥沙在该海域沉积，其他季节海底沉积物在波浪和潮流等海洋动力因素的作用下，进行重新分配。从总体看，西侧以冲蚀作用为主，形成深槽沟，局部有基岩出露，地形起伏较大，表层为第四系滨海相沉积软土，该区软土具高灵敏度、流变性、高压缩性、低强度和不均匀性的特点；东侧以淤积作用为主，地势相对高且较为平坦。该斜坡位于研究区西侧(靠近马德岛)，坡向与管道走向一致，近似东西走向，最大相对高差约15 m，一般坡度为6°，坡脚附近大于10°。

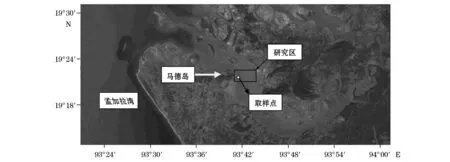
图1 研究区及取样点位置图Fig.1 The study area and sample location

研究区为第三系地层，下伏基岩为第三系中新统(Tm)泥岩(局部砂岩)中新统与下伏老地层不整合接触。研究区所在区域新构造运动表现为整体性隆起。该区域发育2条北西向逆冲断裂，长分别为5 km和13 km。通过卫星解译和野外实地调查，它们都为早中更新世活动断裂。该区域几乎没有强震发生，只有少数中强震发生，对海底斜坡稳定性影响甚微。

在研究区呈近似东西方向布设测线，并设置取样点如图1所示。实测结果表明：该斜坡坡体主要为淤泥、淤泥质黏土，厚度6～9 m。淤泥呈流塑状，土质软，天然含水率高，抗剪强度和固结程度低，在地震、风暴潮、施工扰动等因素影响下，易发生滑移。同时，斜坡东侧存在侵蚀沟槽，海流冲刷发生的沉积物运移，尤其是底流对坡脚的冲蚀，易使斜坡土体逐渐摆脱受力平衡状态，造成边坡失稳。总体评价此斜坡稳定性差，易发生滑坡。

2 模型构建

2.1 稳定性分析模型

2.1.1 模型方程

极限平衡法大都以垂直条分法为基础，通过引入条间力的假定使方程组个数与未知变量个数相同，从而利用力的静力平衡方程求解边坡的抗滑稳定性安全系数。以Bishop法为例介绍模型方程。Bishop法建立了基于垂直方向静力平衡的条块底部法向力方程。在没有孔隙水压力的情况下，Bishop法求解斜坡安全系数的公式为：

(1)

式中，W为土条质量；α为土条底面的倾斜角；c为凝聚力；β为滑块底边长度；φ为内摩擦角。

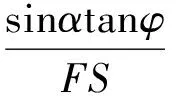
(2)

由于式(1)两边都有FS，必须使用迭代法来求解安全系数。在SLOPE/W中，取瑞典条分法计算的安全系数作为初始值，将这个初始值代入(2)式来计算mα，然后通过公式(1)求得新的FS值，再由这个值计算出新的mα和FS值。如此反复迭代，直至前后两次FS值的差达到容许的精度为止。

2.1.2 模型设置

计算采用加拿大GEO-SLOPE公司研发的岩土工程分析软件GEO-SLOPE中的边坡稳定性计算模块SLOPE/W。其计算原理为极限平衡理论，该模块可以计算考虑孔隙水压力作用下的边坡稳定性。

2011年，依据《海洋调查规范》[16]在研究区取得原状样品，取样点如图1所示，并按照《土工试验规程》[17]对其进行物理、力学指标分析。由于滑体带的抗剪强度受到多种因素的影响，因此认为一点甚至多点的试验值并不能准确代表滑体带的实际抗剪强度。工程地质类比是通过分析与斜坡所处的地质环境类似的滑坡的特征，得到拟求斜坡的参数。根据试验分析结果，并结合工程地质类比分析，本次计算选取计算参数如表1所示。

表1 土体物理力学参数表Table 1 Physical and mechanical properties of soil

根据上述计算方法及参数，结合浅地层调查得到的斜坡区地形及地层特征(图2)，对该斜坡稳定性问题创建模型如图3所示。其中，表层虚线为海平面，第一层为淤泥，第二层为淤泥质粘土，第三层为基岩。

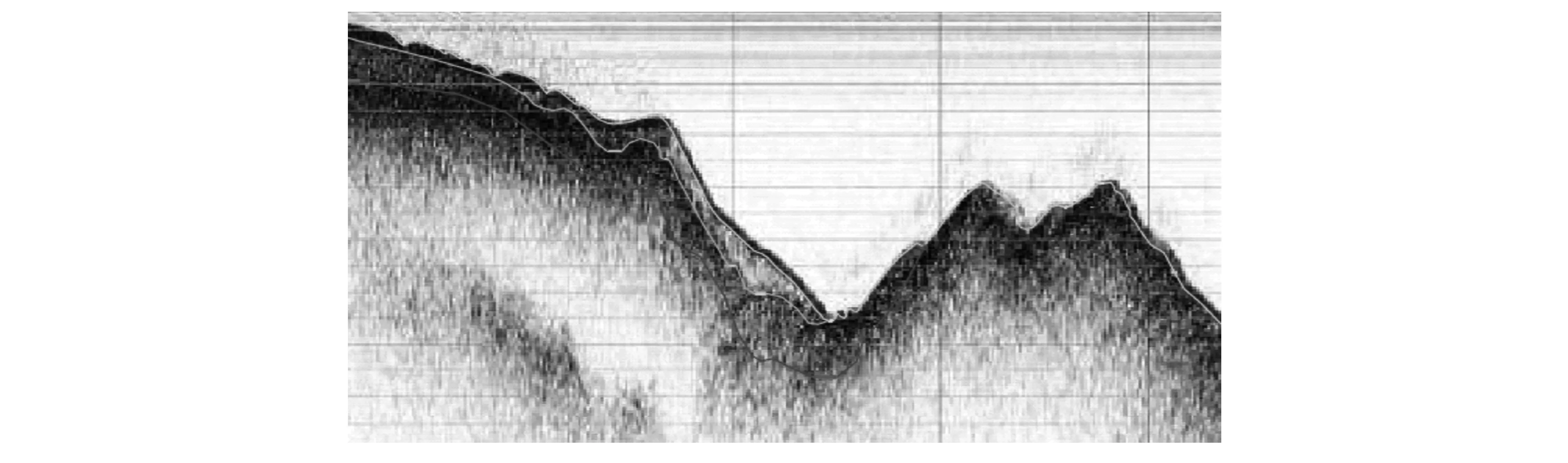
图2 斜坡区浅地层剖面影像Fig.2 Sub-strata seismic profile showing the submarine slope

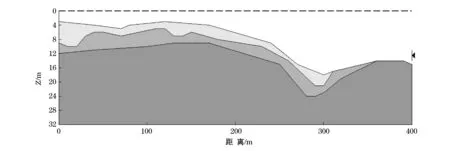
图3 海底斜坡稳定性计算断面Fig.3 The profile for calculating the stability of submarine slope

2.2 滑移距离计算模型

2.2.1 模型方程

海底斜坡土体失稳后应该用流体力学的方法对滑体的特征进行研究[18]。BING采用的3种经典的流变模型为：Bingham流变模型、Herschel-Bulkley模型、双线型流变模型，其中Bingham流变模型[19]可以归类到Herschel-Bulkley模型中。经典流变模型如图4所示。

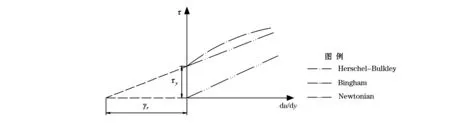
图4 流变模型Fig.4 The rheological model used in the present study

Herschel-Bulkley模型如下式[20-21]：

(3)

式中，τ为剪切应力；τy为屈服剪切应力；γ为应变率，γ=du/dy；u表示沿x方向的流速；γr为参考应变率γr=(τy/μ)1/n，μ为动力粘度。当n为1时该模型就转化为Bingham模型。

双线型模型不属于粘塑性流变模型，其剪切应力与应变率的关系如下：

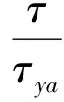
(4)

式中，τya为表观屈服剪切应力。r=γr/γ0。γr，γ0为与应变率高低有关的参数。

式(3)与式(4)结合斜坡土层的质量守恒方程、动量守恒方程[14]，可对碎屑流的流速进行计算。

2.2.2 模型构建

计算采用Imran等所编写的一套利用有限差分数值方法来计算海底滑坡的软件——BING。该软件将滑动面假定为抛物线形式，碎屑块体将沿着指定的地形破坏、扩散。此软件没有考虑“滑水”现象[15]。

为了更加全面准确地表达碎屑流在海底面的流动和传播，图5给出了斜坡所在地500 m范围内断面的海底地形数据。图中，A点与B点高程差约为4 m，C点与D点高程差约为2 m。

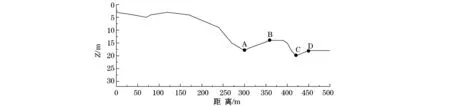
图5 斜坡区500 m范围内海底地形Fig.5 Submarine topography of the slope within 500 m seaward from the shore

将滑动体的原始赋存状态、土体特性参数以及数值计算参数输入界面，并将上图所示地形数据导入，便可构建海底滑坡碎屑流的滑动距离的计算模型。

3 结果与讨论

3.1 稳定性结果分析

利用SLOPE/W模块中的“SOLVE”命令对问题进行求解，得到较为严谨的Morgenstern-Price法(简称M-P法)的安全系数，同时在SLOPE/W中还可查看Ordinary、Bishop和Janbu三种方法的安全系数。在考虑孔压与否的不同条件下，4种方法计算所得斜坡的最小安全系数见表2。

表2 斜坡稳定性安全系数计算成果Table 2 Calculation results for the safety factor of slope stability

查看M-P法计算得到的最小安全系数对应的危险滑动面(图6)，由图可知最危险滑动面在距计算原点200～300 m处，边坡稳定性安全系数为0.606。

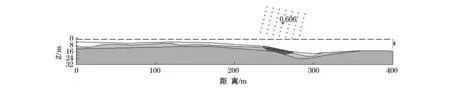
图6 海底斜坡最危险滑动面及最小安全系数Fig.6 The most dangerous sliding surface and minimum safety factor of the submarine slope

对计算结果进行分析，可知：

1)SLOPE/W的4种稳定性计算方法所得到的安全系数均有所不同，但差异不大，这主要是由于每种方法所做出的假定不同所致(表2)。

2)通过对比是否考虑孔隙水压力的安全系数可知，在考虑孔隙水压力的情况下，4种计算方法计算得到的安全系数均有所下降，其中M-P法安全系数由0.690降为0.606，说明孔隙水压力的存在，降低了海底斜坡稳定性。

3)在考虑孔隙水压力的情况下，Morgenstern-Price法计算所得安全系数为0.606，说明斜坡局部处于不稳定状态，具备演变为滑坡的潜在危险。该最危险滑动面水平长度约为40 m，厚度最大约为7 m，滑坡后壁距计算原点约238 m。

3.2 滑移距离结果分析

将滑动体的原始赋存状态、土体特性参数、斜坡地形数据和数值计算参数等输入界面，分别用Herschel-Bulkley模型和双线型模型对该潜在滑动面的滑动距离进行计算，结果如图7、图8所示。图7显示的是滑动结束时滑坡土体在各个位置上的厚度分布，图8表示滑动发生时，不同滑动前缘位置对应的滑动速率。

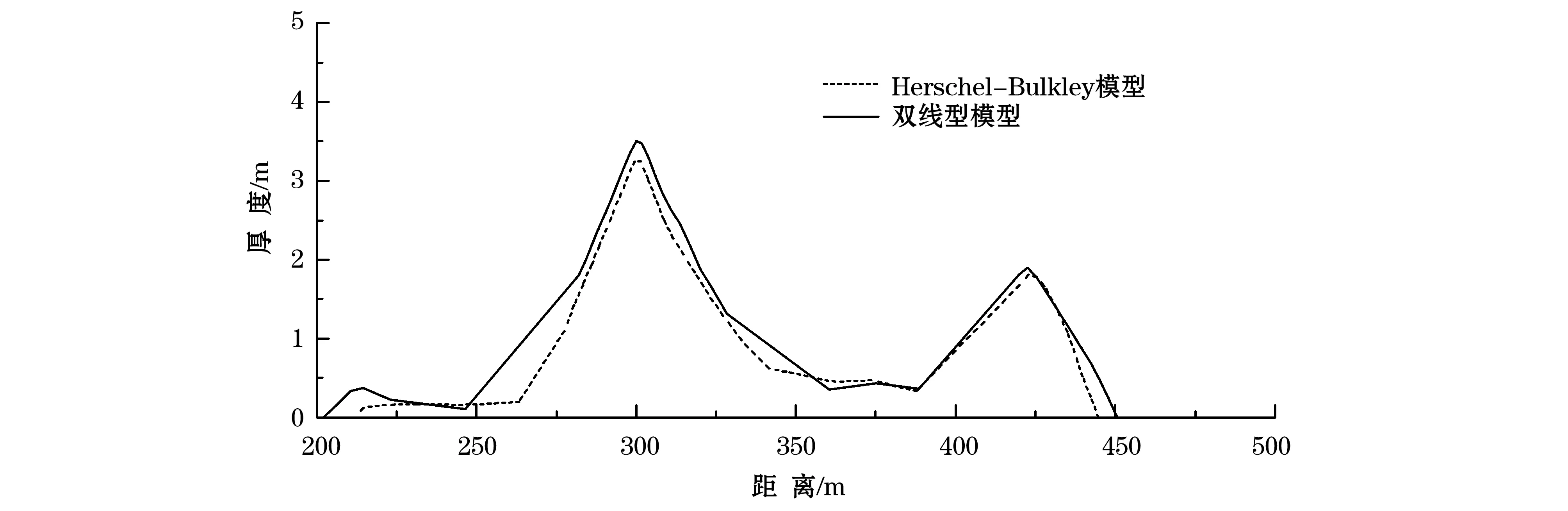
图7 滑动结束时滑坡土体沿滑动方向厚度图Fig.7 The variation of the debris's thickness along sliding direction when the sliding process is ended

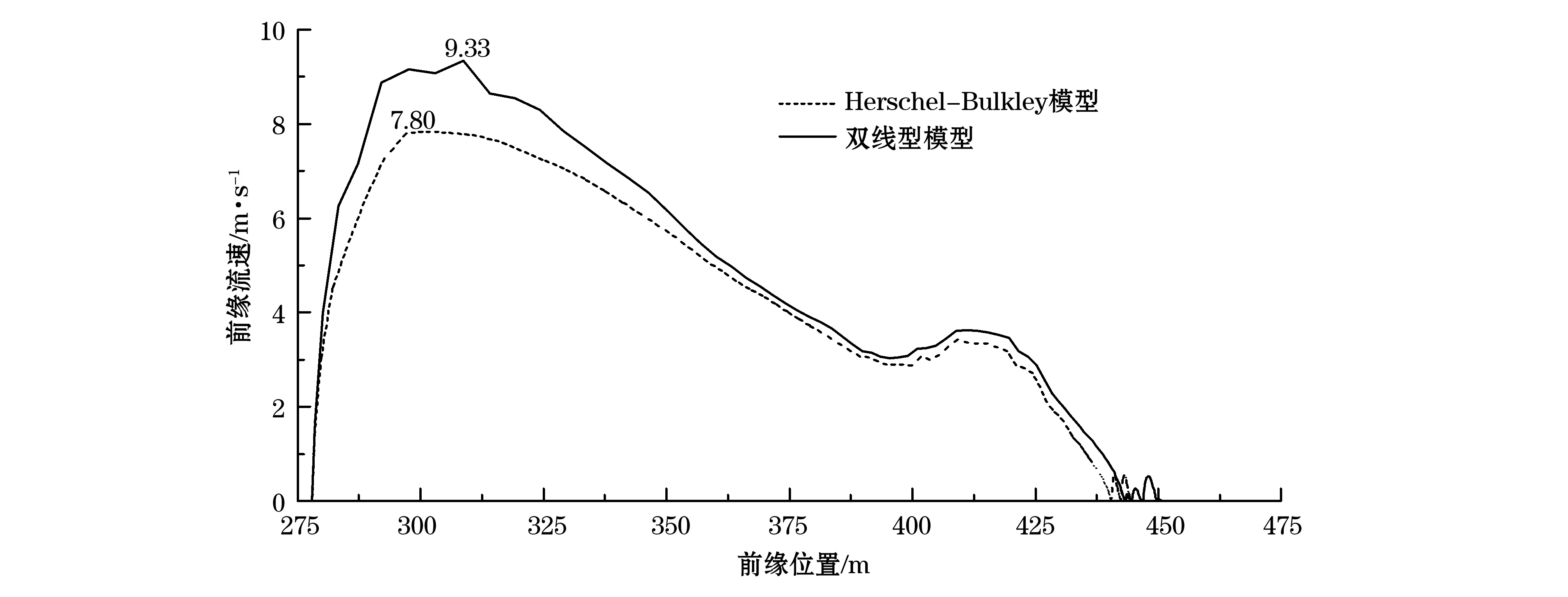
图8 滑坡土体前缘流速随前缘位置的变化曲线图Fig.8 Curves showing the relationship between location and velocity of the front of debris flow

对计算结果进行分析，可知：

1)Herschel-Bulkley模型和双线型模型模拟的滑坡结束时前缘位置分别为445和451 m，滑移距离分别为207和213 m(图7)。滑动土体均没过斜坡东侧的侵蚀沟槽(图5点A处)，停留在C、D两点(图5)之间。滑动土体厚度在300 m和420 m处达到峰值，这与地形起伏是一致的。两种计算方法差异不大。

2)Herschel-Bulkley模型、双线型模型模拟的土体滑动速度分别在297和308 m处达到峰值，峰值速度分别为7.80和9.33 m/s(图8)。400 m过后，滑动速度略有上升，这主要是由地形起伏(图5)决定的。

4 结 论

1)在考虑孔隙水压力状况下，基于GEO-SLOPE中的Morgenstern-Price法计算得到，该斜坡稳定性安全系数为0.606，处于不稳定状态，发生滑坡的概率很大。孔隙水压力的存在降低了海底斜坡稳定性。

2)通过BING软件的Herschel-Bulkley模型、双线型模型模拟计算得到：该斜坡潜在滑动面的滑移距离分别为207和213 m，将没过侵蚀沟槽继续前进；最高滑动速率分别为7.80和9.33 m/s，会对较大范围的海底管道以及其他海底设施造成破坏性影响。

3)斜坡不稳定性不仅仅取决于沉积物性质和地形坡度，地震和波浪对海底的附加压力对斜坡不稳定性也有直接影响[22]。尽管GEO-SLOPE和Bing软件在初步评价海底滑坡稳定性方面有效，但数值模拟方法本身并不完善，仅仅考虑了部分影响因素，有待进一步提高和完善。

[1] LOCAT J, LEE H J. Submarine landslides: advances and challenges [J]. Canadian Geotechnical Journal, 2002, 39(1): 193-212.

[2] MOHRIG D, WHIPPLE K X, HONDZO M, et al. Hydroplaning of subaqueous debris flows [J]. Geological Society of America Bulletin, 1998,110 (3): 387-394.

[3] SHAN R J. Analyse slope's stability of pump with the limited equilibrium method and the finite element method[D].Liaoning: Liaoning Technical University,2009:1-7. 单儒娇.极限平衡法和有限元法分析排土场边坡稳定性[D].辽宁：辽宁工程技术大学，2009:1-7.

[4] CHU X S, PANG F, LI L,et al. Comparative study on FEM strength reduction method and limit equilibrium method for the slope stability analysis [J]. Yellow River, 2011,33(10):93-95.褚雪松，庞峰，李亮，等.边坡稳定有限元强度折减法与极限平衡法对比[J].人民黄河，2011,33(10):93-95.

[5] FELLENIUS W. Calculation of stability of earth dams[C]∥Transactions of the 2nd congress on Large Dams, Washington D. C,1936,4:445-463.

[6] BISHOP A W. The use of the slip circle in the stability analysis of slopes[J].Geotechnique, 1955,5(1):7-17.

[7] JANBU N. Application of composite slip surface for stability analysis[J]. European Conference on Stability Analysis, Stockholm,1954,3:39-43.

[8] SPENCER E. A method of analysis of the stability of embankments assuming parallel inter-slice forces[J].Geotechnique,1967,7(1):11-26.

[9] MORGENSTERN N R ,PRICE V E. The analysis of the stability of general slip surfaces[J].Geotechnique,1965,15(1):79-93.

[10] FREDLUND D G, KRAHN J. Comparison of slope stability methods of analysis[J]. Canadian Geotechnical Journal,1977,14(3):429-439.

[11] ZHANG H Y, CHEN Y M, GONG L L. Stability analysis and evaluation to a slope based on geo-slope software[J]. Shanxi Architecture,2007,33(13):99-100. 张海云，陈义民，巩立亮.基于geo-slope软件对某边坡的稳定性分析评价[J].山西建筑,2007,33(13):99-100.

[12] ZHAO W X. The study of geologic hazards and the quantitative analysis of submarine landslides based on the Geo-Slope software in Chengdao area[D].Qingdao: Ocean University of China,2005:46-65.赵维霞.埕岛海区地质灾害及基于GEO-SLOPE的滑坡定量分析[D].青岛：中国海洋大学，2005:46-65.

[13] QIN K X, FENG W K, LANG Q L.Application of GEO-SLOPE software in calculation of landslide stability[J]. Journal of Catastrophology, 2007,22(2): 21-24. 秦凯旭，冯文凯，郎秋玲. GEO-SLOPE软件在某滑坡稳定性计算中的应用[J].灾害学，2007,22(2): 21-24.

[14] IMRAN J, HARFF P, PARKER G. A numerical model of submarine debris flow with graphical user interface[J]. Computers and Geosciences,2001，27:721-733.

[15] MIAO C Z. Submarine slide and its influence on the submarine pipeline[D].Hangzhou: Zhejiang University,2007:26-41.缪成章. 海底滑坡及其对海底管线的影响[D]. 杭州：浙江大学，2007:26-41.

[16] GB/T12763-2007 Sepecifications for oceanographic survey[S]. Beijing:Standards Press of China, 2002. GB/T12763-2007 海洋调查规范[S].北京：中国标准出版社,2002.

[17] SL237-1999 Specification of soil test [S]. Beijing: China Water & power press, 1999. SL237-1999 土工试验规程[S].北京：中国水利水电出版社,1999.

[18] NOREM H，LOCAT J，SEHIELDROP B. An approach to the physics and the modeling of submarine flowslides [J]. Marine Geotechnology，1990，9:93-111.

[19] JIANG L, LEBLOND P. Numerical modeling of an underwater Bingham plastic mudslide and the waves which it generates[J]. J.Geophys. Res., 1993，98(C6):303-317.

[20] HUANG X,GAREIA M. A perturbation solution for Bingham-plastic mud flows[J]. ASCE Journal of Hydraulic Engineering,1997,120:1350-1363.

[21] HUANG X,GAREIA M. A Herschel-Bulkley model for mud flow down a slope[J].Journal of Fluid Mechanics,1998,334:305-333.

[22] YANG L Q. The stability evaluation and elements analysis of submarine landslides[D].Dalian: Dalian University of Technology,2012:2-39.杨林青. 海底斜坡稳定性及滑移影响因素分析[D]. 大连：大连理工大学，2012:2-39.

NumericalAnalysisforStabilityofSubmarineSlopeoftheMADEKYUNRiverDeltaintheBayofBengal

ZHOU Qi-kun1, SUN Yong-fu1, HU Guang-hai1, YUAN Shun-xin2, DING Ji-sheng1, ZHANG Hai-quan1

(1.TheFirstInstituteofOceangraphy,SOA, Qingdao 266061, China;2.ChinaPetroleumPipelineEngineeringCorporation, Langfang 065000, China)

This study analyzed the geomorphology and strata's lithology in the slope area of the MADE KYUN river delta in the Bay of Bengal. The results, combined with actual survey data, have been used to determine the composition and character of the slope as follows. The slope is mainly composed of mud and muddy clay with the thickness of 6m to 9m. Based on the SLOPE/W mode in GEO-SLOPE software, this study calculated the safety factor of slope stability and determined the most dangerous sliding surface. And, this study predicted the runout distance of the most dangerous sliding surface by using Herschel-Bulkley model and Bilinear model in BING software. The above numerical analysis results showed under considering the pore pressure, the safety factor of slope stability calculated by 4 different methods decrease in some degree, and the slope's safety factor calculated by Morgenstern-Price is 0.606 suggesting its unstable state. The runout distance calculated by two different models is 207 m and 213 m, respectively, and the maximum runout velocity is 7.80 m/s and 9.33 m/s, respectively. Therefore, the slide behavior of the slope may make damage to the submarine facilities such as the submarine pipeline.

Bay of Bengal; GEO-SLOPE; submarine stability; BING; runout distance

February 24, 2014

2014-02-24

国家海洋公益性行业科研专项——近海海底地质灾害预测评价及防控关键技术研究(201005005)

周其坤(1989-)，男，山东临沂人，硕士研究生，主要从事海洋地质灾害与工程安全方面研究.E-mail:zhouqikun05@126.com

(陈 靖 编辑)

P736

A

1671-6647(2014)03-0355-08