求解0-1背包问题的萤火虫算法

刘艺兰，徐丽红，吴丰彦，潘淑静

(中国传媒大学计算机学院，北京 100024)

0 引言

背包问题(Knapsack Problem，KP)是一种组合优化的NP完全问题，也是运筹学中的一个典型的优化难题，有非常广泛的实际应用背景，如运输中的货物装载、人造卫星的物品装载、预算控制以及项目选择等问题，很多整数规划问题的解决理论上都依赖于高效的背包问题解法［1］。一般的背包问题在整数、有界的条件下可转换成等价的0-1背包问题(0-1 Knapsack Problem)，0-1背包问题还可用于研究动态自适应多媒体处理方法［2］、基于用户迁徙网络的广告投放策略［3］等方面，因此研究0-1背包问题有非常重要的实际意义。

关于求解0-1背包问题的算法，很多学者都进行了研究，例如差异演化算法［4］、遗传算法及其相关改进算法与混合算法［5-7］、改进人工鱼群算法［8］、量子蚁群算法［9］、模糊粒子群算法［10］、细菌觅食算法［11］、烟花算法［12］等。本文则使用萤火虫算法来研究0-1背包问题，萤火虫算法有2种:GSO(Glowworm Swarm Optimisation)和FA(Firefly Algorithm)，文献［13］经过实验对比说明了2种萤火虫算法的可行性，并且寻优精度整体上优于粒子群优化算法，而且萤火虫算法参数少，实现简单，因此可以使用萤火虫算法来研究0-1背包问题。文献［14］已设计并使用改进的GSO算法针对0-1背包问题进行了求解，并取得了较为满意的效果，本文则使用另一种萤火虫算法——FA来求解0-1背包问题。

下面对0-1背包问题进行描述:给定n个重量为{W1，W2，...，Wn}价值为{P1，P2，...，Pn}的物品和一个容量为V的背包，0-1背包问题是求这些物品中的一个最有价值的子集，并且要能够装到背包中。设变量xi表示第i种物品是否装入背包，xi=1表示装入背包，xi=0表示不装入背包，则0-1背包问题的数学模型如下:

1 萤火虫算法(FA)

1.1 简介

萤火虫算法是一种新型的仿生群智能优化算法，是受自然界中的萤火虫通过荧光进行信息交流这种群体行为的启发演变而来的［13］。萤火虫算法目前的2种版本，GSO是由印度学者Krishnanand等人［15］在2005年提出的，FA是由剑桥大学Xin-She Yang教授［16］在2008年提出的。本文使用FA来对0-1背包问题进行求解。

1.2 原理

自然界中的萤火虫会发出荧光，以此来吸引异性、捕食或作为警戒信号等。萤火虫优化算法利用该原理，将搜索空间中的可行解模拟为萤火虫个体的位置，将搜索和优化过程模拟为萤火虫个体通过吸引进行位置移动和更新的过程，每个萤火虫位置的优劣取决于其所代表的可行解对应的目标函数值，将萤火虫个体的优胜劣汰过程模拟为搜索和优化过程中用较好可行解取代较差可行解的迭代过程［17］。

1.3 流程

算法中使用到的字母符号及其所代表的意义如表1所示。

表1 字母符号说明表

(1)初始化基本参数(n，β0，γ，α，m)。

(2)随机初始化萤火虫的位置，计算目标函数值作为其最大萤光亮度I0。

(3)计算萤火虫的I和β，确定移动方向。

(4)更新萤火虫的空间位置。公式如下:

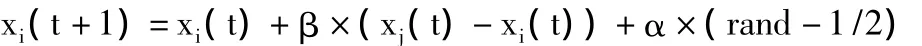
(5)重新计算萤火虫的亮度。

(6)若达到最大迭代次数则转下一步;否则，迭代次数增加1，转(3)。

(7)输出结果。

算法的时间复杂度为O(n2)，n为萤火虫数目。

2 求解0-1背包问题的萤火虫算法

将萤火虫算法应用到0-1背包问题时，每个萤火虫个体的位置就是0-1背包问题的一个可行解向量，该向量的每个分量取0或1，第i个萤火虫位置的第j个分量取0(或1)就代表该萤火虫位置所代表的可行解是将第j个物品不装入(或装入)背包中。决定每个萤火虫位置优劣的目标函数值是其所代表可行解的物品总价值，总价值高的萤火虫能够吸引总价值低的萤火虫向其移动，如此经过多次迭代与移动就能够优胜劣汰。

将萤火虫算法应用到0-1背包问题的过程中，还需要考虑以下几方面的内容。

2.1 离散化

因为0-1背包问题的所有可行解都只包含0、1两种状态，因此本文参考文献［14］以0.5为分界点，在初始化位置和每一次迭代更新位置后，对每个萤火虫的位置进行离散化处理:

2.2 可行化

初始化位置和每一轮位置的更新、离散化后，得到的解未必可行，因为对于0-1背包问题，物品的总重量是有限制的，若某个解的总重量超过了限制，则为不可行解。对于每一轮可能存在的不可行解，本文参考文献［14］，利用贪心策略将不可行解可行化，使搜索总是在可行解空间上进行，同时在保证解的可行性的前提下，尽量增加其适应度值。不可行解xi可行化的过程如下:按物品的单位重量价值由小到大的方向将xij=1变为xij=0，直至将不可行解变为可行解。

2.3 多样化

为了增加萤火虫种群的多样性，本文借鉴遗传算法的变异策略，对每一轮萤火虫的位置在更新、离散化之后，对荧光亮度最低的萤火虫进行变异处理，以增加萤火虫种群的多样性。变异的策略也是前面所述的贪心策略:对于荧光亮度最低的萤火虫xi，按物品的单位重量价值由大到小的方向找到一个xij=0将其变为xij=1。

2.4 算法流程

综上所述，求解0-1背包问题的萤火虫算法的流程大致如下:

(1)初始化基本参数。设置萤火虫数目n，最大吸引度β0，光强吸收系数γ，步长因子α，最大迭代次数m。

(2)随机初始化萤火虫位置。xij=rand。

(3)离散化。将(2)中随机初始化的萤火虫位置以0.5为分界点进行离散化。

(4)按照贪心算法机制将不可行解可行化。

(5)计算每个萤火虫的目标函数值作为各自最大荧光亮度I0。

(6)计算萤火虫之间的吸引度β。

(7)根据I0确定萤火虫的移动方向，根据(6)中计算出的β更新萤火虫的空间位置，对处在最佳位置的萤火虫进行随机扰动。

(8)对更新后的萤火虫位置进行离散化。

(9)计算每个萤火虫更新位置后的目标函数值作为各自最大荧光亮度I0。

(10)对荧光亮度I0最小的萤火虫，按照贪心策略进行变异。

(11)将进行变异后的萤火虫种群位置可行化。

(12)若满足最大迭代次数，则跳出循环迭代，进行下一步;否则，迭代次数加1，转至步骤(5)，进行下一次位置的更新。

(13)输出结果。

求解0-1背包问题的萤火虫算法的流程如图1所示。

3 仿真实验结果及分析

3.1 实验内容

本文运用Microsoft Visual Studio 2010软件，将上述解决0-1背包问题的萤火虫算法用C++语言编写程序进行实现，进而验证算法的运行效果。

根据以下问题的规模以及相关文献的一般取值，算法的初始参数设置如下:萤火虫数目n=6，最大吸引度 β0=1.0，光强吸收系数 γ=1.0，步长因子 α =0.2。

测试数据有3组:

例1 20个物品，背包容量为 878，W={92，4，43，83，84，68，92，82，6，44，32，18，56，83，25，96，70，48，14，58}，P={44，46，90，72，91，40，75，35，8，54，78，40，77，15，61，17，75，29，75，63}［14］。最优解总价值为1024。

图1 求解0-1背包问题的萤火虫算法流程图

例2 50个物品，背包容量为300，W={71，34，82，23，1，88，12，57，10，68，5，33，37，69，98，24，26，83，16，26，18，43，52，71，22，65，68，8，40，40，24，72，16，34，10，19，28，13，34，98，29，31，79，33，60，74，44，56，54，17}，P={26，59，30，19，66，85，94，8，3，44，5，1，41，82，76，1，12，81，73，32，74，54，62，41，19，10，65，53，56，53，70，66，58，22，72，33，96，88，68，45，44，61，78，78，6，66，11，59，83，48}。最优解总价值为1063。

例3 80个物品，背包容量为 800，W={3，68，24，80，76，9，24，2，46，75，56，41，95，46，23，34，64，76，6，48，25，73，87，67，58，7，93，66，55，75，38，27，53，6，100，36，26，17，53，88，21，9，34，90，32，47，4，6，57，50，30，25，41，24，12，74，92，17，32，96，35，76，52，93，64，55，1，70，26，35，2，97，82，22，41，37，63，28，90，13}，P={38，16，29，47，22，25，17，49，15，15，75，11，56，99，51，92，59，37，13，98，61，50，32，17，44，79，41，53，45，29，62，64，2，23，31，45，57，68，57，26，51，26，86，83，94，20，98，24，91，89，1，63，21，46，74，56，64，72，58，8，74，24，27，35，94，49，65，21，16，25，1，45，63，4，37，25，39，68，49，11}。最优解总价值为2085。

3.2 结果分析

3.2.1 实验结果

例1 最大迭代次数m=40，程序运行结果为{1，1，1，1，1，1，1，0，1，1，1，1，1，0，1，0，1，1，1，1}，总重量为837(小于878)，总价值为1018，与真正的最优解(1024)虽不一致，但比较接近。

例2 最大迭代次数m=40，程序运行结果为{0，1，0，0，1，0，1，0，0，0，0，0，0，0，0，0，0，0，1，0，1，0，0，0，0，0，0，1，0，0，1，0，1，0，1，0，1，1，1，0，0，1，0，1，0，0，0，0，0，1}，总重量为 295(小于 300)，总价值为1058，与真正的最优解(1063)虽不一致，但比较接近。

例3 最大迭代次数m=90，程序运行结果为{1，0，1，0，0，1，0，1，0，0，0，0，0，1，1，1，0，0，1，1，1，0，0，0，0，1，0，0，0，0，1，1，0，1，0，0，1，1，0，0，1，1，1，0，1，0，1，1，1，1，0，1，0，1，1，0，0，1，1，0，1，0，0，0，1，0，1，0，0，0，0，0，0，0，0，0，0，1，0，0}，总重量为 792(小于800)，总价值为2081，与真正的最优解(2085)虽不一致，但比较接近。

综上所述，使用萤火虫算法求解0-1背包问题是可行的，而且效果较为良好，故对于属于组合优化NP难题的0-1背包问题，又多了一种可行、有效的解决方法。

3.2.2 参数分析

萤火虫算法中有几个基本的参数，在上述仿真实验中基本参数是在初始化时就给定的。下面参考文献［18］对这几个基本参数进行研究，主要有萤火虫数目n、最大吸引度β0、光强吸收系数γ、步长因子α和最大迭代次数m，主要分析这几个参数的变化对算法性能和最终解的影响。下面基于例1，依次改变这几个参数的值来进行分析。

(1)萤火虫数目n。

最大吸引度 β0=1.0，光强吸收系数 γ =1.0，步长因子α=0.2，最大迭代次数m=40。

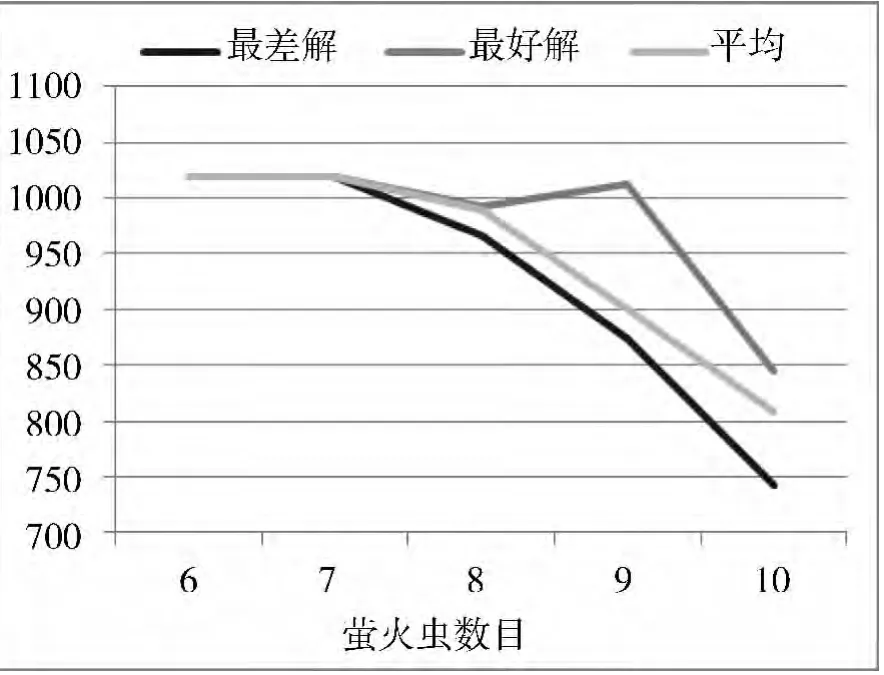
图2 不同萤火虫数目实验结果对比

种群规模是影响萤火虫算法优化精度和收敛速度的重要参数之一，由图2可以看出，在其他所有参数都相同的情况下，萤火虫数目越多，则要聚集到一块就需要较多的迭代次数，故算法的收敛速度越慢，但是数目多的话可以提高解的优化程度;反之萤火虫数目越少，聚集到一起所需的迭代次数就相对少，收敛速度较快，但解的质量会相应地降低。

(2)最大吸引度β0。

萤火虫数目n=6，光强吸收系数γ=1.0，步长因子α=0.3，最大迭代次数m=40。

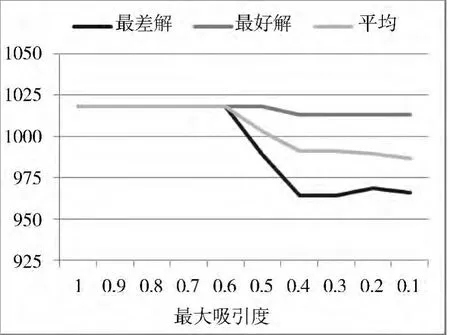
图3 不同最大吸引度实验结果对比

最大吸引度是每个萤火虫自身所处位置(即光源处)的吸引度，它通过影响吸引度β来影响每轮萤火虫移动的距离及算法的收敛速度等。由图3可以看出，在其他所有参数都相同的情况下，最大吸引度越小，算法的收敛速度越慢;最大吸引度越大，算法的收敛速度越快。这是因为最大吸引度越小，每轮萤火虫移动的距离就越小，要想聚集到一起就需要通过较多的迭代次数进行位置的移动和更新，收敛速度慢;相反最大吸引度越大，聚集到一起所需的迭代次数就越少，收敛速度快。

(3)光强吸收系数γ。

萤火虫数目n=6，最大吸引度β0=1.0，步长因子α=0.7，最大迭代次数m=40。

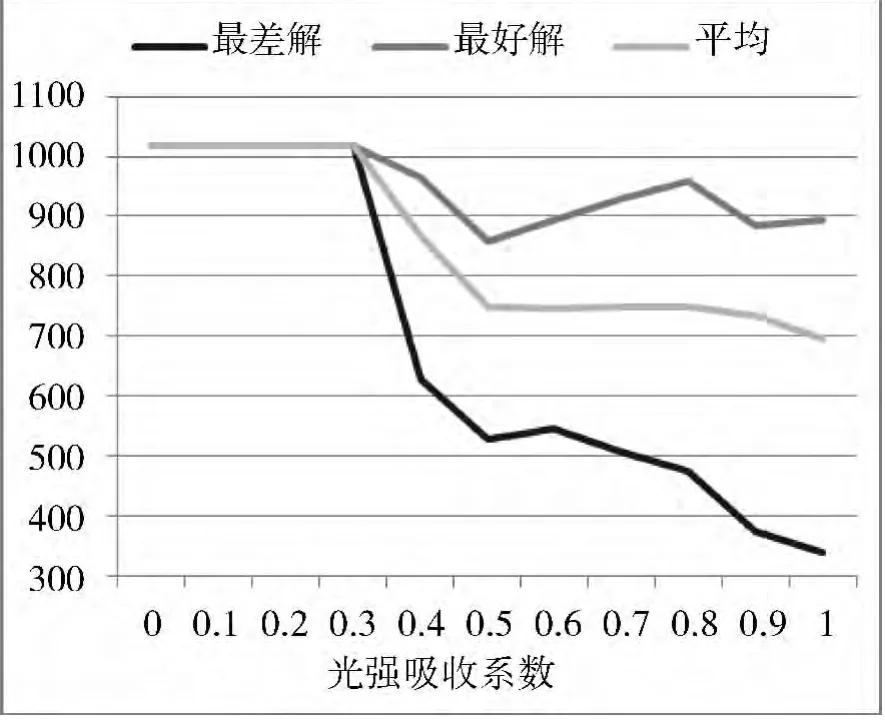
图4 不同光强吸收系数实验结果对比

与最大吸引度相似，光强吸收系数γ对吸引度β影响较大，直接决定了萤火虫个体的移动距离大小、收敛速度和算法的运行。由图4可以看出，在其他所有参数都相同的情况下，光强吸收系数越小，算法的收敛速度越快;光强吸收系数越大，算法的收敛速度越慢。其原因也是光强吸收系数对每轮萤火虫移动距离的影响，只不过计算公式中光强吸收系数之前添加了负号，因此光强吸收系数越小，每轮移动的距离反而越大，收敛速度快;而光强吸收系数越大，每轮移动的距离就越小，收敛速度慢。

(4)步长因子α。

萤火虫数目n=6，最大吸引度β0=1.0，光强吸收系数γ=1.0，最大迭代次数m=40。

步长因子的引入是为了加大搜索区域，提高萤火虫种群的多样性，避免算法过早陷入局部最优。步长因子的取值为［0，1］上的常数，应与具体搜索区间范围、位数相关，在较小搜索范围内，α取值过大，有可能导致算法无法收敛;取值过小，随机移动距离极小，无法增加种群多样性，不能起到扩大搜索范围、避免算法过早收敛的作用。在本实验中，取定其他参数后，由图5可知，步长因子越大，收敛速度越慢;步长因子越小，收敛速度越快。由于本实验增加了基于贪心策略的变异操作，因此当步长因子较小时，虽然随机移动极小，但变异操作增加了种群的多样性，扩大了搜索区域，在一定程度上避免了算法过早陷入局部最优，故有较好的收敛效果;而当步长因子越大时，随机移动的距离过大，要收敛就相对比较困难。

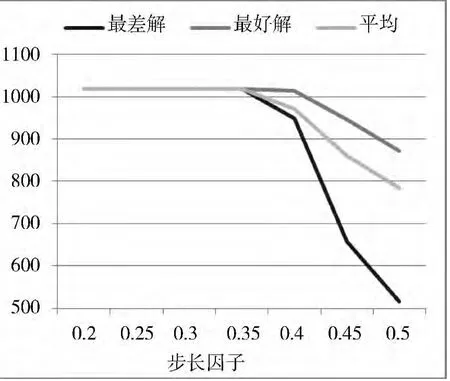
图5 不同步长因子实验结果对比

(5)迭代次数m。

萤火虫数目n=6，最大吸引度β0=1.0，光强吸收系数 γ =1.0，步长因子 α =0.2。

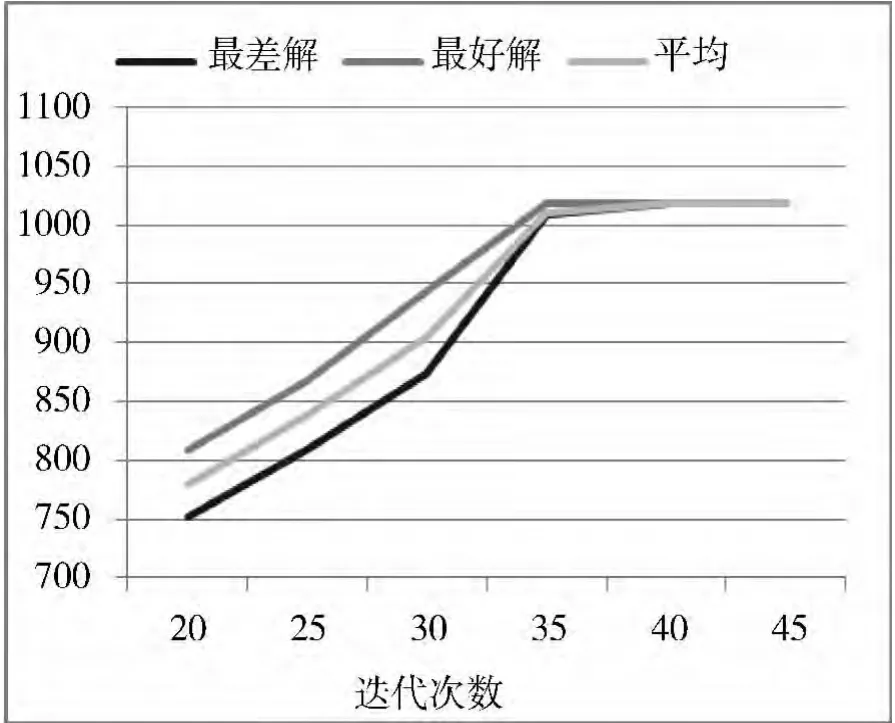
图6 不同迭代次数实验结果对比

迭代次数决定了萤火虫种群要经过多少轮的位置移动与更新才结束算法。由图6可以看出，在其他所有参数都相同的情况下，迭代次数越多，解就越优;迭代次数越少，解就越差。因为萤火虫种群的初始位置是随机选取的，要最终都聚集到亮度高的萤火虫周围需要一定的迭代次数。因此经过较少的迭代次数，萤火虫还没能够从初始位置聚集到亮度高的萤火虫周围，而随着迭代次数的增多，萤火虫种群越来越向荧光高的萤火虫附近聚集，最终就能够聚集到较好的位置。

4 结束语

萤火虫算法是一种新型的群智能优化算法，具有捕捉极值域速度快、捕捉效率高等特点［14］，在生产调度、路径规划等方面具有良好的应用前景。本文将萤火虫算法应用到属于组合优化和NP问题的0-1背包问题中，在Microsoft Visual Studio 2010环境下，使用C++语言编写了算法的程序，并得到了较好的测试结果。不过萤火虫算法还是有很大的改进空间，本文通过多次实验对各个参数对算法性能的影响进行了分析，可以为参数的选取与优化以及算法的改进提供一定的参考与帮助。

:

［1］拓守恒，周涛.一种用于求解0-1背包问题的动态伸缩算法［J］.计算机工程与应用，2012，48(4):47-49.

［2］赵旭.0/1背包问题在动态自适应多媒体处理方法中的应用研究［J］.计算机工程与科学，2011，33(8):154-157.

［3］赵雪梅，周飞菲.基于用户迁徙网络的广告投放策略研究［J］.电脑开发与应用，2013，26(5):5-8.

［4］张欣，王志刚，夏慧明.差异演化算法求解多维0-1背包问题［J］.科学技术与工程，2012，12(6):1278-1280.

［5］吴迪，姜永增，宋广军.基于蜂群遗传算法的0-1背包问题［J］.计算机工程与科学，2011，33(5):102-105.

［6］王娜，向凤红，毛剑琳.改进的自适应遗传算法求解0/1背包问题［J］.计算机应用，2012，32(6):1682-1684.

［7］刘文涛，胡家宝.求解0-1背包问题的改进排挤遗传算法［J］.计算机工程与设计，2011，32(6):2150-2153.

［8］宋潇潇.求解大规模0-1背包问题的改进人工鱼群算法［J］.西华大学学报:自然科学版，2013，32(4):5-9.

［9］何小锋，马良.求解0-1背包问题的量子蚁群算法［J］.计算机工程与应用，2011，47(16):29-31.

［10］柳寅，马良.0-1背包问题的模糊粒子群算法求解［J］.计算机应用研究，2011，28(11):4026-4027.

［11］戴秋萍，马良，郗莹.求解0-1背包问题的细菌觅食算法［J］.数学的实践与认识，2013，43(3):178-183.

［12］张家琴.求解0/1背包问题的烟花算法研究［J］.武汉工程职业技术学院学报，2011，23(3):64-66.

［13］王皓.群智能优化算法——萤火虫算法［J］.科技致富向导，2012(21):158-159.

［14］程魁，马良.0-1背包问题的萤火虫群优化算法［J］.计算机应用研究，2013，30(4):993-994.

［15］Krishnanand K N，Ghose D.Detection of multiple source locations using a glowworm metaphor with applications to collective robotics［C］//Proc.of IEEE Swarm Intelligence Symposium.Piscataway:IEEE Press，2005:84-91.

［16］Yang Xin-she.Nature-inspired Metaheuristic Algorithms［M］.Luniver Press，2008:83-96.

［17］刘长平，叶春明.一种新颖的仿生群智能优化算法:萤火虫算法［J］.计算机应用研究，2011，28(9):3295-3297.

［18］高伟明.萤火虫算法的研究与应用［D］.兰州:兰州大学，2013.