对2014年大纲卷数列压轴题思维断层的思索及探究

浙江省春晖中学，杭州师范大学2012级教育硕士 (邮编：312353)

递推数列一直是竞赛和高考考查的热点和难点，笔者在整理2014年高考中的有关递推数列试题时，发现高考数学大纲卷数列压轴题第(II)问提供的参考答案具有一个明显的思维断层，从而引发笔者的探究兴趣.探究结果显示，该试题尽管形式简洁，却不乏丰富的内涵，值得我们细细回味.为此笔者将探究体会整理成文，以飨读者.

(I)讨论f(x)的单调性；

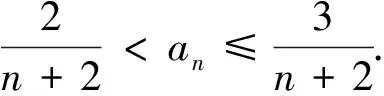
1 思维断层的发现

上述试题命题组给出的参考答案如下.

(I)略，结果为：当12时，f(x)在(-1,0)上单调递增，在(0,a2-2a)上单调递减，在(a2-2a,+∞)上单调递增.

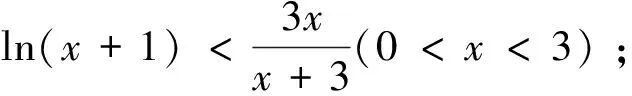
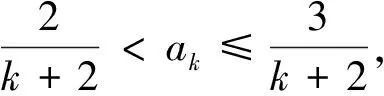
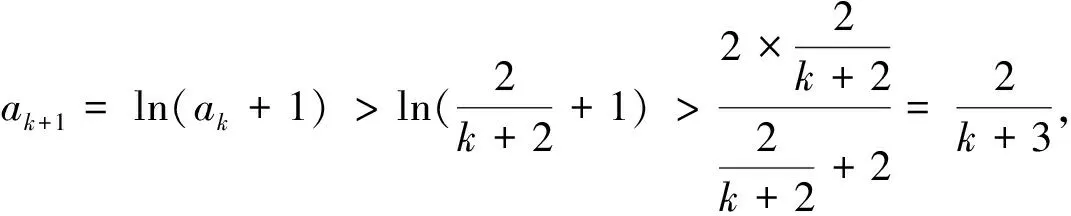
2 对思维断层的思索

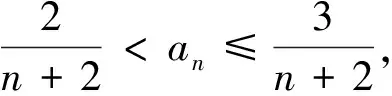
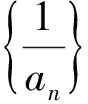
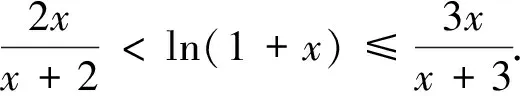
而这恰为参考答案中所呈现的关键不等式.

3 思维断层背后隐藏的别解

基于对上述思维断层的合理诠释，我们可以得到如下更具自然的解法.

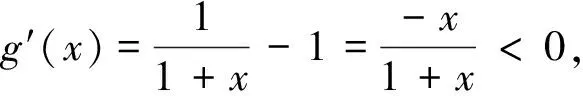
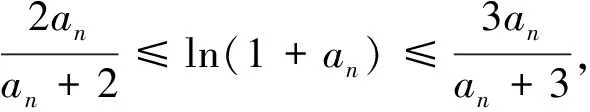
4 基于思维断层思索下试题的纵向加强

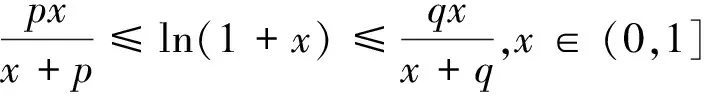
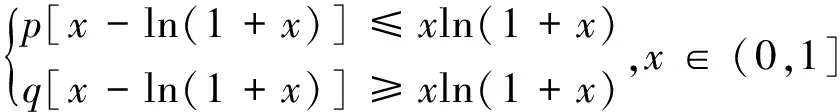
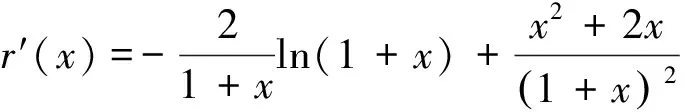
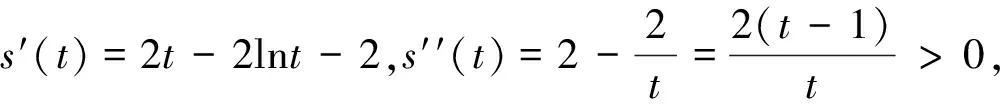
从而s(t)在(1,2)上单调递增，故s(t)>s(1)=0，从而r′(x)>0，故r(x)在(0,1)上单调递增，故r(x)>r(0)=0，故h′(x)>0，从而h(x)在(0,1]上单调递增.

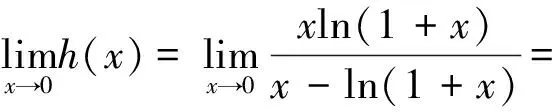
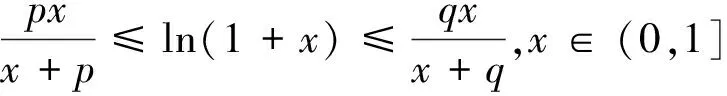
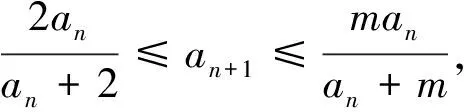
5 基于思维断层思索下试题的横向加强

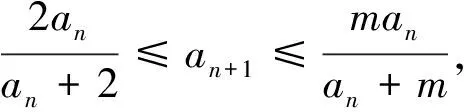
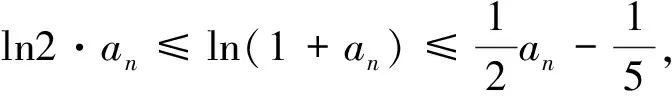
故一方面由ln2·an≤an+1得an≥(ln2)n-1a1=(ln2)n-1；

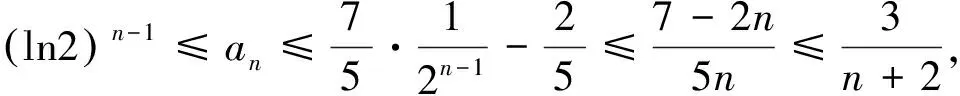
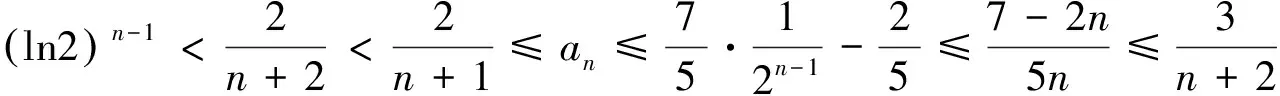
相信通过上述的探究，我们应该能更好地理解原试题及其表象掩盖下的试题本源，也为日后从容应对类似问题提供了宝贵经验，而这正是我们进行教学研究的旨意所在.