圆柱型后体对圆锥垂直入水空泡的影响
2014-08-21黄海龙王柏秋
黄海龙,王柏秋
(1.哈尔滨工业大学土木工程学院,哈尔滨150090;2.北京宇航系统工程研究所,北京100076;3.哈尔滨工业大学建筑学院,哈尔滨150001)
导弹等物体从空中高速进入水中的现象称为入水问题,关于入水问题的研究,最早可以追溯到19 世纪末,A·M·Worthington[1-2]利用高速照相机对液滴和球体入水后所产生的流动现象进行了试验观察,由此开始,各种针对入水空泡问题的探索不断的展开.从文献[3-4]中可以看出,在第二次世界大战前后,多个国家相继利用试验方法和数值方法开展了针对各种导弹、空投鱼雷等武器的入水问题的研究.其中,关于球体入水流场的试验研究[5-9]和基于势流理论研究[10-11]是较多的,其次是关于圆柱体等平头物体[12-14]的研究以及具有圆锥头的柱体模型[15]和射弹模型[16]入水流场的分析.
以上试验研究和理论研究,分别得到了多种航行体的入水阻力系数与各种无量纲参数之间的关系,以及模型弹道等信息.但是,这些试验研究并未讨论模型后体参数的变化情况,例如锥柱体入水问题中,柱体段长度对模型入水空泡的影响.并且,由于研究方法和测试手段的局限性,这些研究成果只能反映入水空泡流场的部分参数信息.因此,随着计算机技术的发展,利用数值计算,直接求解NS方程的方法逐渐得到了蓬勃发展[17-18],这使得所论目标更接近真实,能够获得的流场信息更丰富.
综上所述,带有后体的航行体入水空泡问题研究成果较少,而具有后体的航行体入水产生的空泡流场与不带后体又具有一定差异.因此,针对后体对入水空泡流场的影响问题,本文利用动网格技术,采用VOF多相流模型和有限体积法求解RANS方程,对具有不同柱段长度的锥头圆柱体匀速垂直入水过程进行数值计算,分析模型匀速垂直入水过程中,空泡的生成和发展过程,以及有、无后体和后体长度对入水空泡的影响.
1 控制方程
1.1 试验方法连续性方程和动量方程
混合物连续性方程:

空气相连续性方程:

水蒸气相连续性方程:

混合相动量方程:
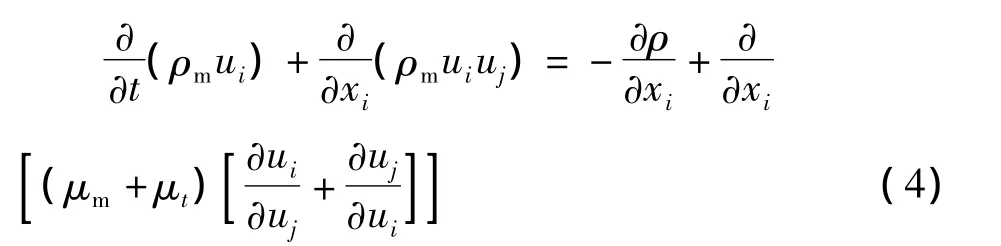
其中:ui表示混合物速度分量,m/s;下标m、l、g和v分别表示混合相、水、空气和水蒸气;ρm为混合物密度(kg/m3);μm是混合物动力黏性系数,m2/s.
其中:ρm和μm分别为:
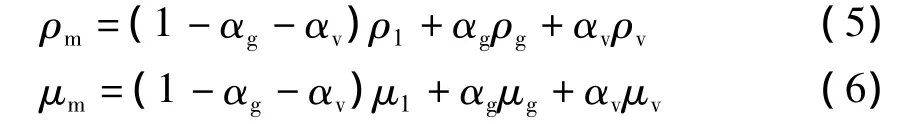
其式中:αg、αv和 -αg、-αv分别为空气、水蒸气和水的体积分数.
1.2 空化模型
高速入水物体在入水过程中产生空泡,仅有物体头部与水接触,在物体头部边缘的分离处会出现较大的压强梯度变化,当压强降低到饱和蒸汽压强之下时,可能会出现自然空化现象.本文将这一复杂过程通过式(7)、(8)中的源项来表示(即Zwart-Gerber-Belamri空化模型).源项表达式如下:
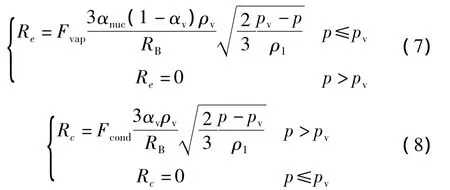
其中:Re、Rc表示水蒸气产生和凝结;RB=10-6m为气泡半径;αnuc=5×10-4,为不可凝结气体体积分数;Fvap、Fcond为经验常数,分别取 50 和 0.001.
1.2 湍流模型
本文计算中采用Realizable k-ε模型模拟湍流,该湍流模型中,湍动能k和湍能耗散率ε的输运方程分别为:

其中:σk和σε分别为k和ε的Prandtl数,取值分别为 σk=1.0,σε=1.2;为由平均速度梯度所引起的湍动能生成项;经验常数C1和C2取值分别为1.44 和1.9.
2 数值求解
2.1 计算域和边界条件
本文选取130°圆锥头型为研究对象,模型后体圆柱直径 D=10 mm.根据A·M·Worthington[1]的研究,轴对称物体垂直入水所产生的空泡流场同样具有轴对称性质,因此,本文数值计算均采用二维轴对称计算模型,计算域设置和模型表面网格分布示意图如图1所示.图1中,空气域高度为60 D,水域深度为400 D,计算域径向为80 D,使用四边形网格划分计算域.不失一般性,在保证计算精度和正确性的基础上,选取网格密度和计算量适中的网格分布作为本文数值模型.
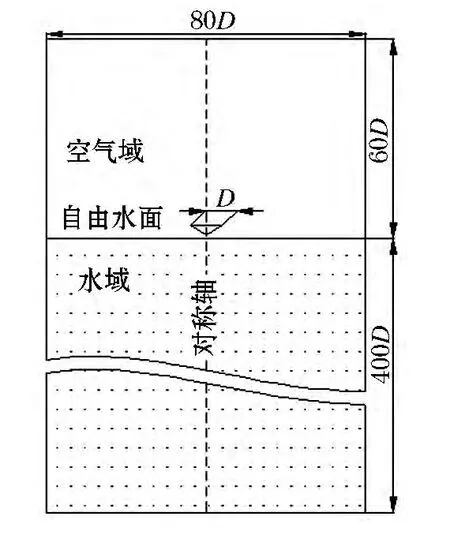
图1 圆锥及计算域分布示意图
2.2 数值方法
本文采用有限体积法对控制方程进行空间离散,应用PISO方法对动量方程方程和连续性方程联立求解.计算过程中,对流项的离散采用二阶迎风格式;水蒸气相的离散采用QUICK格式;湍流输运方程的离散采用二阶迎风格式;对时间的离散采用一阶显示格式.计算时间步长的选取根据网格尺度、运动速度等因素综合确定.通过动网格技术实现模型的运动过程与计算域内的网格更新.
由于本文计算采用结构化网格,网格主要是被拉伸或被压缩变形,因此,采用动态层分裂法进行网格更新.动态层分裂法的基本思想是当网格被拉伸到大于设定的理想最大尺度((1+αs)hideal)时,该网格分裂成两层新的网格,当网格被压缩到小于设定的理想最小尺度(αchideal)时,网格与其相邻的网格合并成新的网格,即:

引入动态网格后,相当于网格按一定速度作对流运动,在实际计算中应减掉网格的对流效应.因而引入动网格后控制体V对变量φ的统一形式的守恒方程可写为:
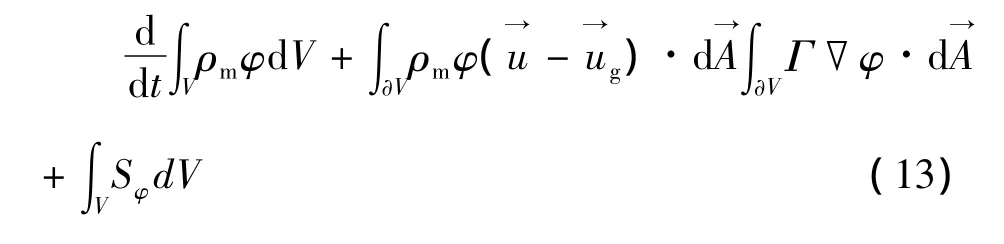
其中:ρm为混合物密度为速度矢量为动网格的运动速度;Γ为扩散系数;Sφ为标量φ的源项;∂V表示控制体积V的边界.
3 数值方法对比与验证
为验证方法的正确性和可信性,首先对直径为25.4 mm球体匀速垂直入水过程进行数值计算,并将计算结果的空泡轮廓与Albert May[6]等人提出的匀速垂直入水理想空泡模型进行对比如下.
在二维轴对称坐标系下,垂直入水早期空泡形态的理想空泡模型表达式如式(14)所示,该入水空泡模型主要用于描述入水过程中,空泡闭合之前发展较为充分时期的外部轮廓.
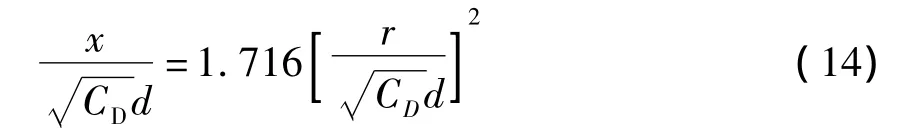
其中:CD为入水物体的阻力系数;d为入水物体的特征尺寸.
模型从空气域匀速垂直入水,入水速度30 m/s,空气域环境压强为101 325 Pa,空气、水、和水蒸气的密度分别为 1.225、998.2、0.554 kg/m3.选取入水空泡充分发展时的空泡形态,与相同时刻下,由式(14)的理想空泡模型拟合结果进行对比,结果如图2所示,其中,阻力系数取CD=0.20.
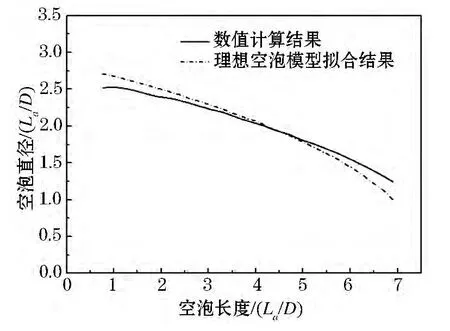
图2 无后体圆锥入水空泡轮廓计算结果与经验公式对比
由图2可以看出,数值计算结果与理想空泡模型拟合结果具有较好的一致性.在空泡轮廓两端具有一定的误差,产生该误差的主要原因是由于理想空泡模型本身忽略了自由表面处和分离点处的空泡轮廓的不规则性.通过图2的对比验证可见,本文所采用的数值计算方法是正确可信的,在此基础之上,下面针对带有不同尺度圆柱后体的圆锥模型,展开匀速垂直入水空泡的数值计算.
4 计算结果分析
计算模型外形如图3所示,顶部锥角 a=130°,直径 D=10mm,后体长度 L分别为:0(圆锥),0.5D,1.0D,2.0D 和 4.0D.为考察后体对入水空泡的影响,将各模型入水计算结果的某一时刻流场分布显示于图4中.
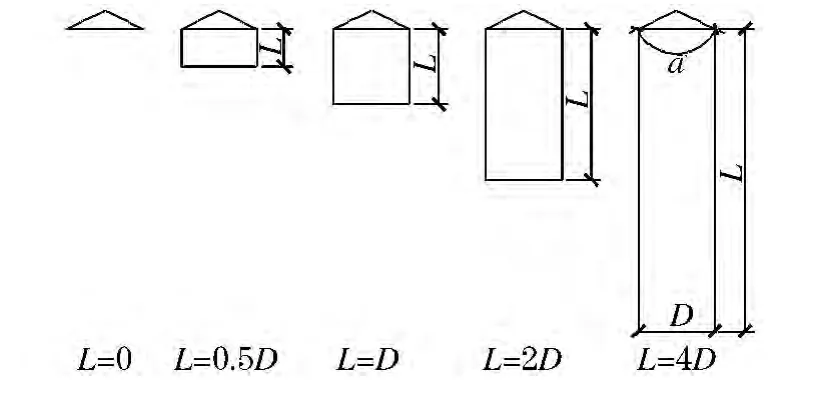
图3 不同长度后体模型
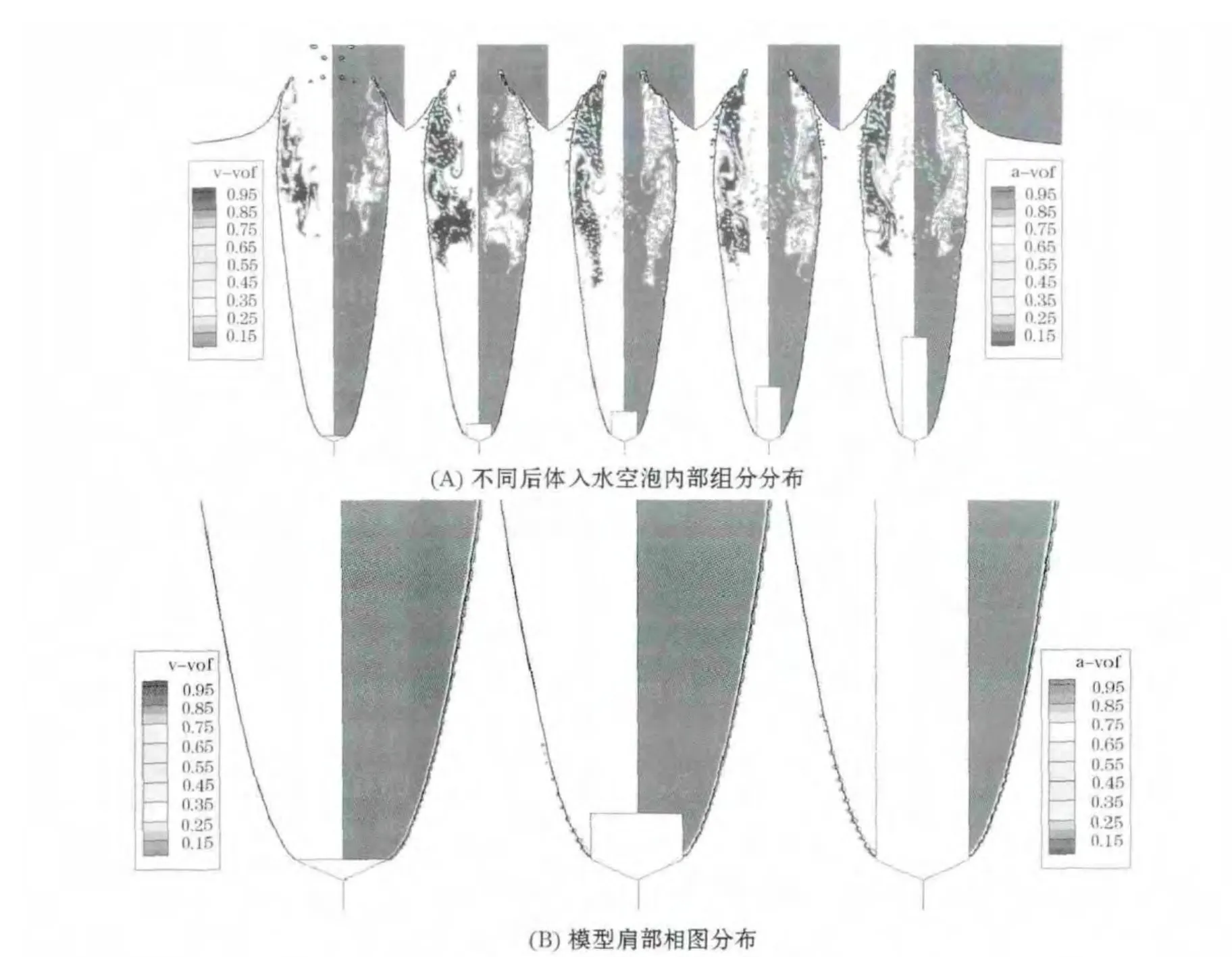
图4 入水空泡内部组分分布
有后体后,可以发现入水空泡的最大直径随着后体尺度有一定变化.图5表示垂直入水空泡最大直径随后体长度的变化过程,入水速度为200 m/s.从图5可以看出,模型后体长度较小时(例如图5中的无后体模型和后体长度为L=0.5D模型),入水空泡最大直径略高于其余带后体模型,随着模型后体长度的增加,入水空泡最大直径逐渐降低,当后体长度增加到一定程度后,入水空泡最大直径趋于稳定,不再随后体长度变化而变化.

图5 空泡最大直径随模型后体的变化
图4中的入水空泡尾部的闭合情况清晰表明入水空泡闭合时间随后体的出现而有所变化.图6表示模型匀速垂直入水过程中,入水空泡尾部无量纲闭合时间随后体长度的变化情况,模型入水速度为200 m/s.
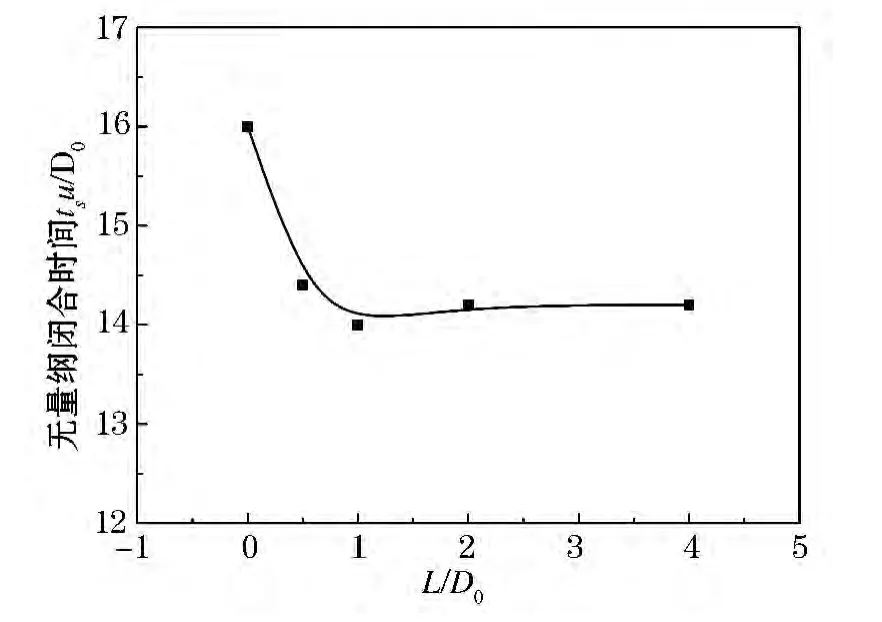
图6 入水空泡闭合时间随后体的变化
从图6可以看出,模型后体长度较小时,空泡闭合时间较长,尤其当后体长度L=0时,闭合时间最长;当模型后体长度较大时,空泡闭合时间趋于一致,例如当L>2.0时,空泡闭合时间不再随后体长度变化而变化.由图5、6可以看出,带后体模型产生的入水过程,当模型后体长度大于某一数值时,流场是相近的.为考察稳定的入水过程,下面以L=4.0D的模型为例,进行分析.
图7为长后体模型(L=4.0D)匀速垂直入水过程中,水蒸气和空气在空泡内部的空间分布的变化情况,其中,模型入水速度为200 m/s.从图7可以看出,在入水初期,模型肩部的流动分离点附近和空泡入口处的喷溅内部边缘有少量的水蒸气.随着入水过程的进行,空泡入口的喷溅液体迅速向内弯曲,空泡开始趋于闭合.此时,在空泡入口处的弯曲液壁内侧,由于液面迅速弯曲,附近流体流速增高,静压力急剧下降,导致液体迅速空化,从而使得该处水蒸气含量随着空泡闭合而迅速增加,随着时间的推移,空化逐渐沿着空泡壁面向空泡内部传播.在模型附近,既空泡头部附近,空泡轮廓线稳定,不随时间变化,因此,该处流场内部压力和流速均稳定,发生空化的概率相对较低,该处只存在少量入水冲击产生的水蒸气或者不存在水蒸气.
另外,由图7的入水过程可知,入水空泡内部流体压力低于外界大气压和周围流体内部静压,当空泡壁运动能量不足时,将导致空泡壁向轴线坍缩,从而挤压内部空气,最终可能导致一股沿空泡轴线向上的液体喷溅的产生.
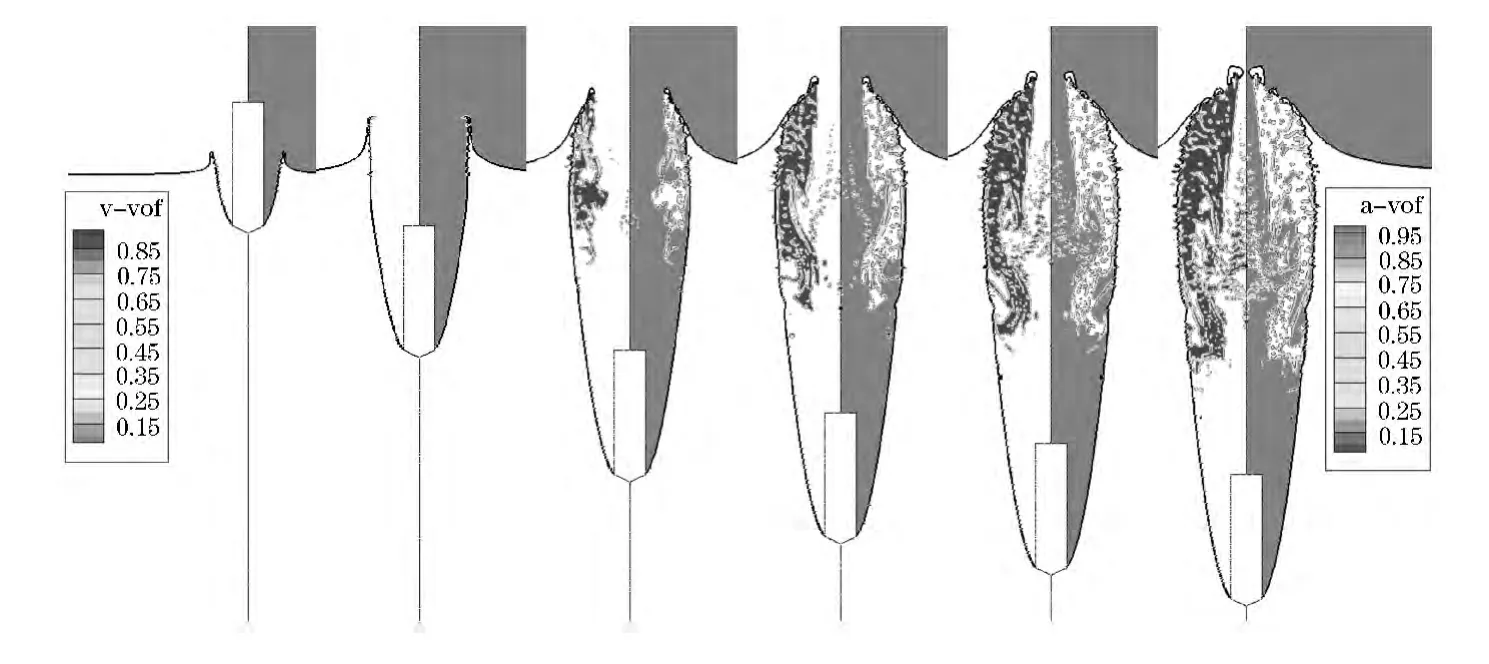
图7 不同时刻入水空泡组分分布
5 结论
本文对具有不同长度圆柱型后体的圆锥匀速垂直入水过程进行了数值模拟研究,分析了有、无后体和不同长度后体模型入水后,空泡的发展过程及空泡内部流场的分布,得到了以下结论:
1)模型在匀速垂直入水后形成的入水空泡内,无后体模型流场内的空化作用弱于有后体模型流场,入水空泡内的水蒸气含量明显偏低.
2)带圆柱后体模型,后体的存在有利于模型肩部流动分离点附近自然空化的发生,并有少量的水蒸气分布在分离点附近的空泡壁面.
3)无后体模型入水空泡的闭合明显晚于带圆柱后体模型入水空泡的闭合,当圆柱后体长度小于1倍圆柱体直径时,空泡最大直径随着后体长度的增加而减小,且空泡最大直径略大于具有更长带后体的模型;当后体长度大于2倍以上圆柱体直径时,入水空泡最大直径与后体长度无关.
4)无后体时,入水空泡的闭合时间较长;有后体时,后体长度大于两倍圆柱直径时,入水空泡的闭合时间与后体长度无关.
通过本文研究可以看出,模型后体的存在对入水空泡形态及相关参数有重要影响,为了使入水问题研究结果在鱼雷和导弹等武器中得到更好的应用,应加强对模型后体影响的研究.
[1]WORTHINGTON A M.A study of splashes[M].New York:Longmans Green and Company,1908.
[2]WORTHINGTON A M,COLE R S.Impact with a liquid surface[J].Phil.Trans.Roy.Soc.,1897,189A:137 -148.
[3]WHALLEY I A.Project upkeep-a review of the WWⅡdambubuster weapon[C]//Indianapolis:38th AIAA Joint propulsion Conf,2002.
[4]ALBERT M.Water entry and the cavity-running behavior of missiles[R].AD A020429,1975.
[5]MALLOCK A.Sounds produced by drops falling on water[J].Pro.R.Soc.Lond.,1918,A95:138 -143.
[6]BELL G E.On the impact of a solid sphere with a fluid surface
[J].Phil.Mag.j.Sci,1924,48:753 - 765.
[7]ASHLEY S.Warp drive underwater[J].Sci.Amer,2001,284(5):70-79.
[8]MAY A,WOODHULL J C.Drag coefficients of steel spheres entering water vertically[J].Journal of Applied Physics,1948,19(12):1109-1121.
[9]TRUSCOTT T T,TECHET A H.Water entry of spinning spheres[J].J.Fluid Mech,2009,625:135 -165.
[10]Yan H,Liu Y,KOMINIARCZUK J,et al.Cavity dynamics in water entry at low Froude numbers[J].J.Fluid Mech,2009,641:441-461
[11]ARISTOFF J M,BUSH J W M.Water entry of small hydrophobic spheres[J].J.Fluid Mech,2009,619:45 -78.
[12]SHI H,ITOH M,TAKAMI T.Optical observation of the supercavitation induced by high-speed water entry[J].Journal of Fluids Engineering,2000,122:806-810.
[13]何春涛,王 聪,何乾坤,等.圆柱体低速入水空泡试验研究[J].物理学报,2012,61(13):1-8.
[14]陈学农,何友声.平头物体三维带空泡入水的数值模拟[J].力学学报,1990,22(2):129-138.
[15]王 聪,何春涛,权晓波,等.空气压强对垂直入水空泡影响的数值研究[J].哈尔滨工业大学学报,2012,44(5):14-19.
[16]MAY A.Effect of surface condition of a sphere on its waterentry cavity[J].Journal of Applied Physics,1951,22:1219-1222.
[17]HE C,WANG C,WEI Y,et al.Numerical simulation of pressure distribution in vertical water- entry cavity[J].Journal of Ship Mechanics,2011,15(9):960 -968.
[18]何春涛,王 聪,闵景新,等.回转体匀速垂直入水早期空泡数值模拟研究[J].工程力学,2012,29(4):237-243.
