随机域最大值的几乎处处中心极限定理

汪园芳，吴群英

（桂林理工大学理学院，广西 桂林541004）

0 引言及定义

设｛X，Xn；n≥1｝是一个独立同分布的随机变量序列成立，如果此式满足，则有最简单形式的几乎处处中心极限定理成立，即：

其中，I（A）是事件A的示性函数，Φ（x）是标准正态分布函数.对几乎处处中心极限定理的研究可以从两个方面来考虑，一是随机变量序列的扩展，可以将简单的随机变量序列扩展为混合的随机变量序列，或者扩展到随机域；二是权重形式的扩展，可以将简单的权重扩展到加权函数形式的权重.

独立同分布的随机变量序列的部分和形式的几乎处处中心极限定理首次被Brosamler［1］和Schatte［2］引入并证明，从此之后，几乎处处中心极限定理被推广到各种不同的形式.特别地，Fahrner等［3］以及Cheng［4］将部分和形式的几乎处处中心极限定理推广到最大值形式的几乎处处中心极限定理，Csaki等［5］将几乎处处中心极限定理应用到平稳高斯序列，Dudzinski［6］将部分和形式的几乎处处中心极限定理推广到部分和和最大值的形式，Hyemi［7］将几乎处处中心极限定理从平稳高斯序列推广到平稳高斯域，但对非平稳高斯域的几乎处处中心极限定理的研究文献较少，本文中研究在协方差满足一定的条件下，获得独立同分布的随机域的最大值的加权函数形式的几乎处处中心极限定理.

记Nd为d维正整数集，k＝（k1，…，kd）∈Nd，l＝（l1，…，ld）∈Nd，n＝（n1，…，nd）∈Nd，｜n｜＝n1…nd，而且k≤l意味着ki≤li，i＝1，…，d，并且当 max1≤i≤dni→∞，对某些时认为n→∞.如果当n→∞时则记an～bn；如果存在某常数c＞0使得对于充分大的n，有an≤cbn，则记成an≪bn.

1 定理及引理

定理 设｛Xi；i∈Nd｝是独立同分布的，且具有零均值以及有限方差的随机域，同时对∀γ＞0满足

则对任意的分布函数G（x），有下面两式等价：

其中代表着G（x）的连续点集.

引理1［8］设ξ1，ξ2，…为一组有界的随机变量序列，如果存在某ε＞0，使得成立，则有成立的情况下，如果0≤d＊k≤dk，并且满足则有

引理2［8］在 成立.

注记 由引理2可以推出，定理1对小的权重成立，则定理1对大的权重也成立.

2 定理的证明

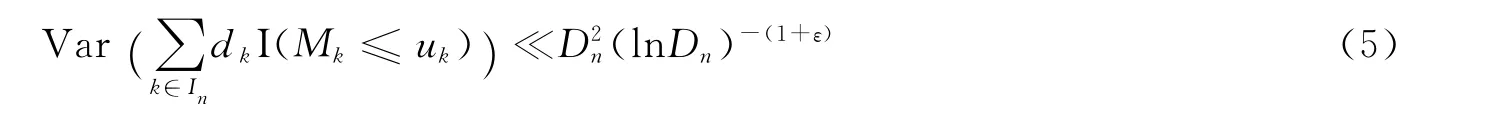
令ξk＝I（Mk≤uk）-P（Mk≤uk），其中，k，l∈Nd，则由（1）式和（2）式，我们有：

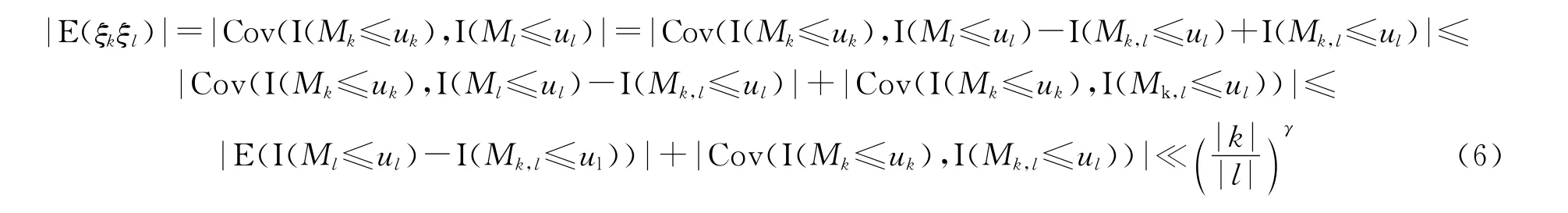
令n＝（n1，…，nd），定义则有：

由于E（ξ2k）是有界的，并且exp（2（lnki）β）是慢变化函数，则有：

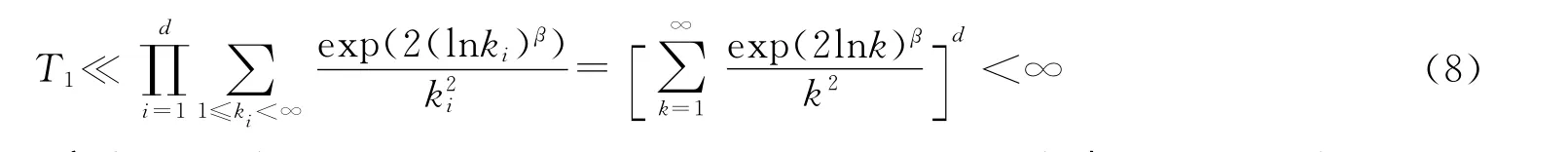
进一步地，为了估计T2，定义Am＝｛（k，l）∈Ⅰn×Ⅰn：（2mi-1）（ki-li）≥0，k≠l｝以及m∈Δ≡｛（m1，…，md）：mi＝0，1，i＝1，…，d，m≠1｝，则由（6）式和（7）式，有：

下面，先估计mi＝0这种情况下的T2.根据Am的定义，当mi＝0时，很显然可以得出ki≤li，进一步可以得出：

然后来估计mi＝1这种情况下的T2.和上面的情况类似，根据Am的定义，当mi＝1时，很显然可以得出ki≥li，则可得到：

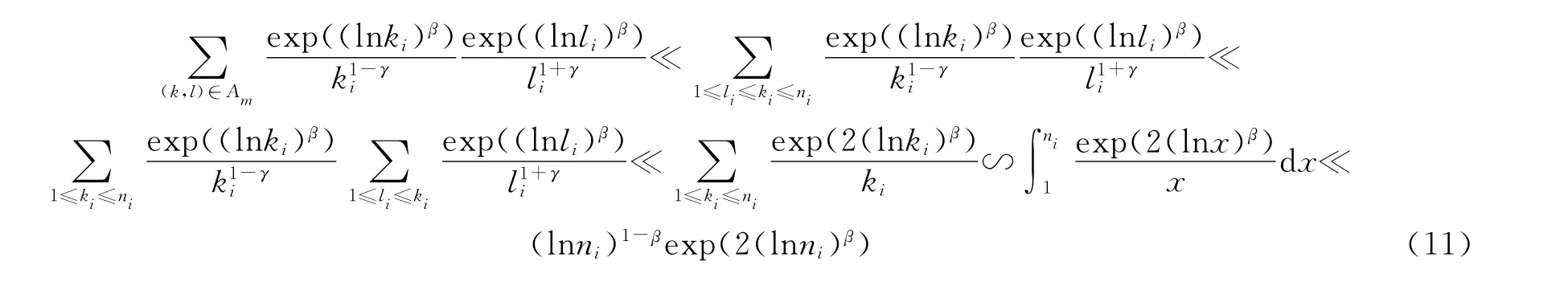
因此，综合mi＝0和mi＝1两种情况下的T2的估计，我们可以归结为：

由文献［10］中可以得到下面的等价式：

由（12）式和（13）式可以推得：

然后将上面的估计带入（9）式，进而有：

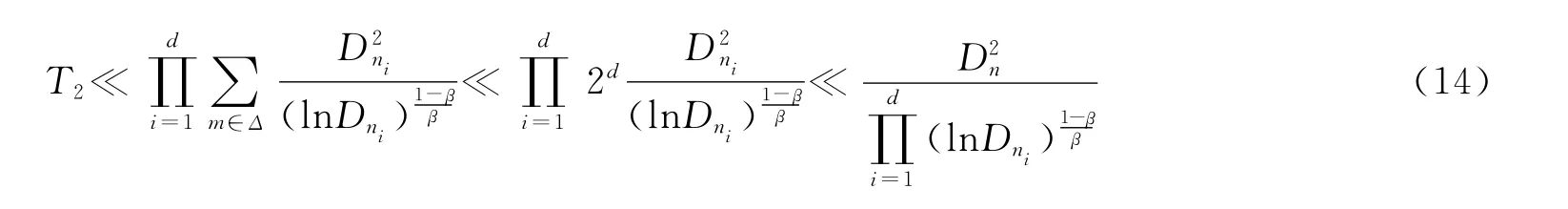
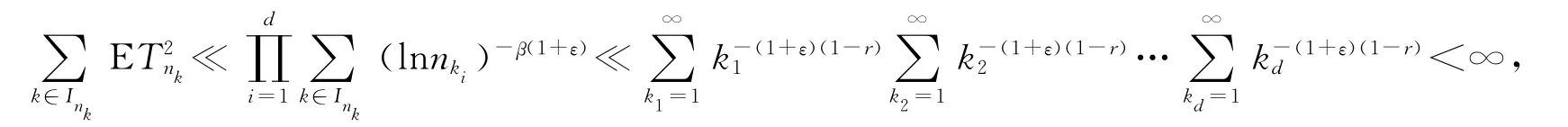
由Borel-Cantelli引理［9］知：

由于ξk＝I（Mk≤uk）-P（Mk≤uk），很显然，ξk是有界的，对于n＝（n1，…，nd），nk＝（nk1，…，nkd），nk＋1＝（nk1＋1，…，nkd＋1），特别地，对于ni存在一个序列ki使得nki＜ni≤nki＋1，1≤i≤d成立.则对于Tn，有：

注意，

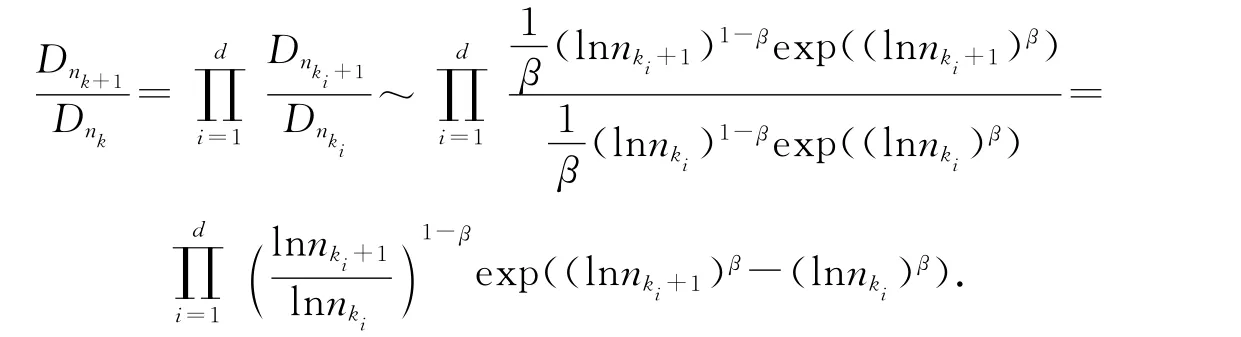
即：

最后，由（18）～（20）式得到：

［1］Brosamler G A.An almost everywhere central limit theorem［J］.Math Proc Cambridge Philos Soc，1988，104：561-574.

［2］Schatte P.On strong versions of the central limit theorem［J］.Math Nachr，1988，137：249-256.

［3］Fahrner I，Stadtmuller U.On almost sure central max-limit theorems［J］.Stat Probab Lett，1998，37：229-236.

［4］Cheng S H，Peng L，Qi Y C.Almost sure convergence in extreme value theory［J］.Math Nachr，1998，190：43-50.

［5］Csaki E，Gonchigdanzan K.Almost sure limit theorems for the maximum of stationary Gaussian Sequences［J］.Statist Probab Lett，2002，58：195-203.

［6］Dudzinski M.The almost sure central limit theorems in the joint version for the maxima and sums of certain stationary Gaussian sequences［J］.Statist Probab Lett，2008，78：347-357.

［7］Hyemi Choi.Almost sure limit theorem for stationary Gaussian random fields［J］.JKSS，2010，39：449-454.

［8］Wu Qunying.Almost sure central limit theory for products of sums of partial sums［J］.Math Appl J Chinese Univ，2012，27：169-180.

［9］吴群英.混合序列的概率极限理论［M］.北京：科学出版社，2006.