基于特征约束的LiDAR点云等高线自动生成方法
2014-08-20,
,
(武汉大学 遥感信息工程学院,武汉 430079)
1 研究背景
传统的等高线提取主要基于摄影测量和地面测量。提取原理是首先通过空间后方交会或从星历中解算出影像的外方位元素,然后进行影像匹配得到同名点的像坐标,最后通过前方交会解算出地面点空间三维坐标后内插得到格网DEM,根据DEM生成等高线。传统方法效率低且成本高,由于需要大量人工操作,受人的经验因素影响较大。
随着LiDAR(Light Detection and Ranging)技术的发展,利用LiDAR数据自动提取等高线的方法应运而生,弥补了传统方法的不足。这类方法主要基于高程格网或TIN的等高线跟踪方法。如Batcha等[1]提出离散点内插成规则格网或根据离散点建立三角网,再从规则格网或三角网上跟踪提取等高线的方法;王涛等[2]提出一种优化高程格网内插等高线的方法。由于LiDAR点云密度大,为避免内插的方法导致精度损失,保证地面精度,一般采用基于TIN的等高线跟踪方法,如Boissonnat[3]的加密算法。根据国家成图规范,等高线不能穿过建筑物、水系地物等所在的约束区域。传统基于TIN的等高线跟踪方法一般采用人工编辑处理约束区域的等高线,存在人工劳动强度过大的缺点。本文提出一种基于特征约束的等高线提取方法,先进行特征提取,然后自动生成特征约束的TIN三角网,最后在特征约束TIN的基础上提取等高线。
2 LiDAR点云滤波
LiDAR点云数据是高精度的地表三维点云数据(DSM),它除了包含地面点之外, 还包含地表的地物点,即非地面点。为了获取反映真实地表的DEM,提高等高线精度,需要对DSM点云数据进行滤波,从而去除非地面点,得到裸露的地面点。现有滤波的方法主要是基于激光点的几何特性对地面点和非地面点进行区分,主要有以下3类:①基于形态滤波的方法[4-5]。这类方法的优点是直观,缺点是当地形变化剧烈时,处理效果不够理想;②基于曲面约束的方法。这类方法适用于平坦地形,对于地形起伏剧烈的山区效果不佳,且计算量大,运行效率较低;③基于内插的方法[6]。这类方法原理清晰,计算简单,能较好处理地形起伏较大的山区,但要求预先剔除粗差。
本文数据采自长阳山区,地形较为复杂、建筑物较多,为满足TIN算法对DEM精度的要求,本文采用改进的渐进加密三角网滤波算法[7]。为验证改进的渐进加密三角网滤波的有效性,将试验区点云数据分别利用形态滤波方法和基于曲面约束的滤波方法分别进行处理,并与改进的渐进加密三角网滤波法的滤波结果对比。通过比较几种滤波方法产生的第1类错误即将地面点判为非地面点和第2类错误即将非地面点判为地面点,对滤波效果进行定量评价。为了更好地分析每种方法的滤波效果,本文分别对平地、山区、建筑物区和植被区这4种典型地形区域进行滤波处理和分析,其结果如表1。本文试验所用LiDAR数据采自长阳山区,有平地、山地及建筑物,且植被覆盖率较高、地形起伏较大、地物构成比较复杂。由表1可知,采用稳健性较强的改进渐进加密三角网滤波法效果最优,采用该方法得到的DEM三维渲染图如图1所示。
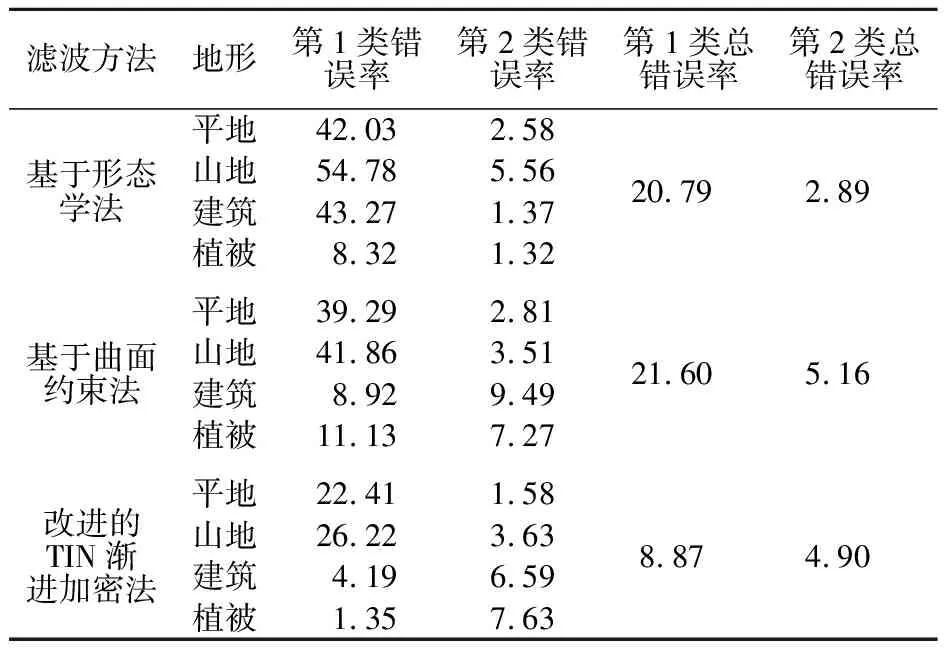
表1 滤波错误率

图1 DEM三维渲染图
3 特征提取
特征约束区域提取是生成特征约束TIN三角网的基础,通常通过提取典型地物的边缘信息可得到典型地物的特征约束区域。在基础测绘生产应用中,建筑物和水系这2类地物的边缘特征最为典型,本文重点介绍建筑物及水系的边缘提取方法。
3.1 建筑物
目前基于LiDAR数据进行建筑物提取的方法有很多,这些方法主要可以分为2类:第1类是基于原始点云再处理的建筑物激光点提取法(如崔建军[8],任自珍[9]),这类方法的缺点是在再处理的过程中无法避免地引入了不必要的误差。第2类方法是基于滤波分类的建筑物激光点提取法。这类方法的代表是区域增长法(如Nicholas等[10])。此类方法以真实的数据为基础,边缘提取精度和可靠性较高,因此本文采用第2类方法。
(1) 在TIN形式的DEM中,建筑物区域常对应边长较大的三角形。利用建筑物区域三角形的边长较大的特性,设定适当的阈值,可提取出建筑物区域,得到建筑物点云。
(2) 建筑物区域边缘跟踪。α-shapes[11]算法可以高效地提取各类建筑物边缘。
3.2 水 系
水系所在区域的点云数据具有点密稀疏、高程相近、回波强度弱和水面低于周围陆地的特点。基于水系在点云数据上的以上4个特征,采用直接利用LiDAR点云数据提取水系轮廓线的方法[12]。该方法首先利用单层粗格网提取水域。将满足水系点云4个特征条件的格网块判断为水系的格网块;再利用双层格网提取较窄的水域。双层格网的处理可以使得较窄的河流不易断裂,在连通去噪后还能保留下来。单层及双层格网的示意图如图2所示。
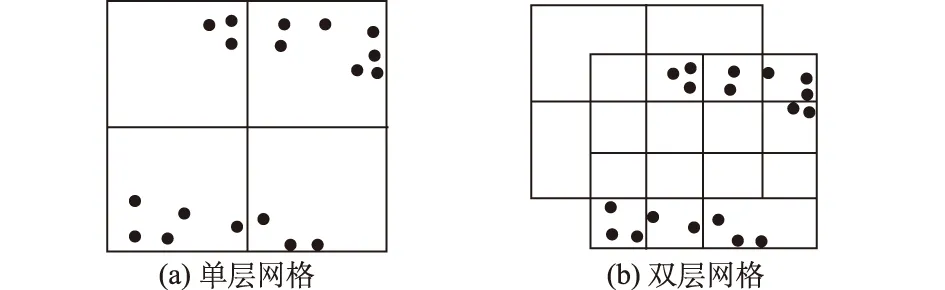
图2 单层及双层格网示意图
在水体格网提取的基础上,通过拉普拉斯边缘提取算子获得边缘格网,求出各个边缘格网中面向水系的边缘点,试验区数据覆盖的主要水系为长阳的清江,其边缘提取结果见本文4节中的图3中深蓝色曲线所示。

图3 建筑物区域的约束TIN
4 基于特征约束的三角网TIN生成
本文第3节提取的建筑物及水系边缘线所围成的区域即为特征约束区域,将在约束区域内生成的三角网自动删除,就能得到约束三角网。常用的建立约束三角网的方法很多,如:基于约束图的CDT构造算法[13],非约束数据域Delaunay三角剖分的分割合并算法[14],加密算法[3],2步法[15-16]等。2步法处理方式更灵活且效率更高,因此本文采用2步法建立约束三角网。其结果如图3所示。右上角图为红色框内区域的放大显示。紫色线为建筑物边缘线,蓝色线为水系边缘线,建筑物和水系边缘线围成区域内的三角网被剔除。
5 基于特征约束TIN的等高线生成
依据基础测绘线画图产品规范,等高线不能穿过建筑物和水系。且在第4节中,已将建筑物及水系区域的三角网自动删除,因此,本节将研究在带有特征约束的TIN的基础上,实现等高线的自动生成,其主要流程如下:
(1) 基于约束三角网跟踪等高点。依次判断每条等高线是否与三角形的边相交,将与等高线相交的三角形内插得到等高点坐标,内插公式为
(1)
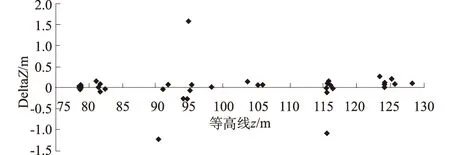
(2)等高线平滑。将所有等高点连接起来得到的是不光滑的折线,需使用光滑算法进行处理以得到光滑等高线。本文采用精度较高的张力样条函数插补法[17],主要原理:设(x1,y1),(x2,y2),…(xn,yn)是一组已知的数据点,且x1 f″-σ2f(x)=[f″(x)-σ2yi](xi+1-x)/Hi+ [f″(xi+1)-σ2yi+1](x-xi)/Hi。 (2) 张力样条数为单值情况下公式(2)的解要得到更精确和美观的曲线,需要设定合适的张力系数值。整个试验区等高线如图4所示,建筑物区域等高线局部放大图右上角所示,可见等高线未穿过建筑物和水系。 图4 建筑物区域等高线 等高线精度检查利用导线测量得到的检查点的高程值与等高线内插出的对应检查点的高程值进行比较,从而得到等高线的高程精度。实验选取52个检查点,以等高线高程Z为横轴,误差DeltaZ为纵轴绘制误差分布散点图,等高线误差分布图如图7所示。其中平均高差为+0.022 m,最小高差为-1.221 m,最大高差为+1.570 m,平均误差为0.145 m,最小二乘残差为0.326 m,方差为0.328 m,满足1∶2 000 DLG成图规范的要求。 图5 等高线误差分布 本文以特征约束的TIN三角网为基础,利用LiDAR点云数据实现长阳山区等高线自动提取。 针对长阳测区数据地形起伏较大,地物构成复杂的特点,采用稳健性较高的改进的渐进三角网滤波方法生成高精度的DEM点云数据,实现地面高程模型TIN三角网的自动生成,并以每个三角网边的长度为约束条件,实现建筑物和水系这2类典型地物边缘的自动提取,同时自动剔除特征区域内的三角网,生成带有特征约束的TIN三角网。在此基础上,判定等高线是否穿越当前三角网,利用三角网顶点高程值内插,自动提取等高线。本文在试验区域选取52个检查点,对生成的等高线进行了精度评价,评价结果表明该方法流程满足1∶2 000 DLG成图规范的要求,与传统的等高线提取方法相比,该方法更具科学性、可靠性,节省了大量人工操作,具有效率快和作业精度高的特点。 但针对以下2种情况:①地形起伏变化剧烈,如悬崖、陡坎等比较丰富的区域;②经过人工改造的平坦区域,如农田、果园、梯田等区域,特征提取需要进一步完善,TIN三角网的生成条件会更加严格,因此等高线的生成算法,有待于进一步研究和完善。 参考文献: [1] BATCHA J, REESE J. Surface Determination and Automatic Contouring for Mineral Exploration, Extraction, and Processing[J]. Colorado School of Mines Quarterly, 1964, 59: 1-4. [2] 王 涛,毋河海.一种从高程格网中提取等高线的算法[J]. 测绘科学,2006, 31(2):108-110. (WANG Tao, WU He-hai. An Algorithm for Extracting Contour from Elevation Grid[J]. Science of Surveying and Mapping, 2006, 31(2): 108-110. (in Chinese)) [3] BOISSONNAT J. Shape Reconstruction from Planar Cross Sections[J]. Computer Vision, Graphics, and Image Processing, 1988 ,(1): 1-29. [4] KILIAN J, HAALA N, ENGLICH M. Capture and Evaluation of Airborne Laser Scanner Data[J] . IAPRS,1996,31(B3) : 383-388. [5] VOSSELMAN G. Slope Based Filtering of Laser Altimetry Data[J]. IAPRS, 2000,(B3) : 935-942. [6] AXELSSO N P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models [J]. IAPRS,2000,33(B4/1) : 110-117. [7] 李 卉,李德仁,黄先锋,等.一种渐进加密三角网LIDAR点云滤波的改进算法[J],测绘科学,2009,34(3):39-41. (LI Hui, LI De-ren, HUANG Xian-feng,etal. An Algorithm for LIDAR Point Cloud Filtering Based on Progressive Encrypting Triangulation[J]. Science of Surveying and Mapping, 2009, 34(3):39-41.(in Chinese)) [8] 崔建军,隋立春,徐花芝,等.基于边缘检测算法的LiDAR数据建筑物提取[J].测绘科学技术学报,2008,25(2):98-100. (CUI Jian-jun, SUI Li-chun, XU Hua-zhi,etal. Building Extraction from the LiDAR Data Based on the Edge Detection Algorithm[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2008, 25(2): 98-100. (in Chinese)) [9] 任自珍,岑敏仪,张同刚,等.基于等高线形状分析的LiDAR建筑物提取[J].西南交通大学学报,2009,44(1):83-88. (REN Zi-zhen, CEN Min-yi, ZHANG Tong-gang,etal. Building Extraction from the LiDAR Data Based on Contour Shape Analysis[J]. Journal of Southwest Jiaotong University, 2009,44(1):83-88.(in Chinese)) [10] NICHOLAS S,TAKIS K.Triangulated,Connected Sets for Building Detection from Irregularly Spaced LiDAR[C]∥ Proceedings of the 3rd International Symposium on Communications, Control and Signal Processing, Malta, March 12-14, 2008: 560-565. [11] 沈 蔚,李 京,陈云浩,等. 基于LIDAR数据的建筑轮廓线提取及规则化算法研究[J].遥感学报, 2008,(5):692-698.(SHEN Wei, LI Jing, CHEN Yun-hao,etal. Algorithm Research Based on Buildings Contour Extraction and Regularization from LIDAR Data[J]. Journal of Remote Sensing, 2008,(5):692-698.(in Chinese)) [12] 王宗跃,马洪超,徐宏根,等.基于LiDAR 点云数据的水体轮廓线提取方法研究[J], 武汉大学学报·信息科学版,2010,35(4) :432-435. (WANG Zong-yue, MA Hong-chao, XU Hong-gen,etal. Research of Water Contour Extraction Based on LiDAR Point Cloud[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4) :432-435. (in Chinese)) [13] LEE D, LIN A. Generalized Delaunay Triangulation for Planar Graphs[J]. Discrete and Computational Geometry, 1986, (1): 201-217. [14] LEE D, SCHACHTER B. Two Algorithms for Constructing a Delaunay Traingulation[J]. International Journal of Parallel Programming, 1980,(3): 219-242. [15] SLOAN S. A Fast Algorithm for Constructing Delaunay Triangulations in the Plane[J]. Advances in Engineering Software, 1987, (1): 34-55. [16] DE FLORIANI L, PUPPO E. An On-line Algorithm for Constrained Delaunay Triangulation[J]. CVGIP: Graphical Models and Image Processing, 1992, (4): 290-300. [17] SCHWEIKERT D. An Interpolation Curve Using a Spline in Tension[R]. USA: Department of Applied Mathematics of Brown University, 1965.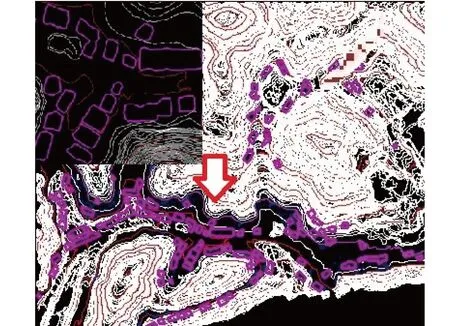
6 等高线精度评定
7 结 语
