基于压水试验的均质含水层渗透系数计算方法
2014-08-18,
,
(长江科学院 水利部岩土力学与工程重点实验室,武汉 430010)
1 研究背景
在水利水电工程中,渗流对工程岩体及构筑物的影响是十分明显的,研究岩石的透水性对大坝渗流、地下硐室开挖等有着极为重要的意义。钻孔压水试验是水利水电工程地质勘察及水工建筑物灌浆工程中常用的一种评估岩体透水性的方法,在水利水电工程中有着广泛的应用。但目前压水试验成果仅提供吕荣值作为衡量岩体透水性的工程指标,该工程指标不便于直接用于水文地质计算。因此通过常规压水试验数据,研究岩体渗透系数的计算方法显得十分重要。
通过压水试验数据计算渗透系数总体上可分为2种方法:一种是将压水试验中每阶段的流量最终值视为稳定流下的流量值,利用承压含水层裘布依(J.Dupuit)稳定井流公式进行计算;另一种则是采用非稳定流方法进行计算。地下水动力学中的非稳定井流理论经过70多年的发展已经比较成熟,可以在压水试验的计算中加以借鉴。S.C.Way和C.R.Mckee[1]提出了利用抽水试验确定三维渗透张量的方法;J.A.Barcker等[2-3]发展了用分维描述的裂隙含水层抽水试验理论;张桢武等[4]采用多孔介质模型提出了定压力变流量和定流量变压力下的压水非稳定流模型。本文从常规吕荣值计算公式出发,分析吕荣值的意义与不足,并采用均质模型分别推导稳定流和非稳定流条件下的渗透系数计算公式,完善压水试验数据的分析计算方法。
2 透水率计算方法
钻孔压水试验中透水率指1 MPa水压力下,1 m钻孔长度内每分钟压入的水量,单位为吕荣(Lu)。用吕荣值表示的透水率在工程中得到广泛的应用,规程[5]中定义的计算公式为
(1)
式中:q为试段透水率(Lu);Q为压入流量(L/min);P为作用于试段内的压力(MPa);L为试段长度(m)。
在压水试验过程中,水是通过试段孔壁渗入岩体的,假定水流方向为垂直于试验段的平行层状渗流,那么入渗流量Q可表示为
Q=Av=2πrwv。
(2)
式中:A为试段的孔壁面积;rw为钻孔半径;v为钻孔孔壁处的渗透流速。
透水率q可表示为
(3)
对于同一试验段,当试段压力P为定值时,在达西定律假定下,其渗透流速v也为定值。因此透水率q可视为孔径rw的函数。即对于同一地层,在不同的孔径下进行压水试验,所得到的透水率是不同的。
在实际工程中,对于不同钻孔半径rw下的透水率q,可设定一标准孔径r′,将不同钻孔半径下的所测得的透水率q转化为单位标准钻孔半径下的岩体透水率q′,即
将实际工程中得到的吕荣值进行孔径标准化处理后,可解决由于不同工程中采用的钻孔半径不同而导致的吕荣值不能直接进行比较的问题,一般可设工程常用的75 mm孔径为标准孔径。
3 基于稳定流假设的渗透系数计算方法及其存在的问题
要通过压水试验结果计算渗透系数,需进行一些必要的假设。本文仅讨论在均质、等厚含水层中进行压水试验,渗流满足达西定律且孔壁出水均匀的情况。并假设渗透流线为水平,即忽略垂直方向上的分量,如图1所示。

图1 压水试验假设条件示意图
当压水试验段处于有限厚度的含水层中,并且其顶板和底板均为相对隔水层时,由于上下均无汇项,垂直方向上的水流仅因单位储水量的增加而引起。对岩体而言,单位储水系数us很小,由单位水头增加所引起的单位储水量的改变较小,因此,在这种情况下垂直方向上的流量是可忽略的。
对于常规压水试验,当注入流量达到稳定后,有
(4)
式中:k为渗透系数;H为压力水头(m);r为压力作用半径(m)。
设压水开始前初始水头为H0,压水试验段压力为Pw(用水柱高度表示,单位为m),则压水开始后孔壁处水压力为H0+Pw。令R为定水头边界的半径,即当压水流量达到稳定时,压水试验的注入流量等于边界R处的流出水量。分离变量积分,取积分限为:压力作用半径r的变化范围为由rw至R,H由H0至H0+Pw,得
(5)
根据上式可得稳定流压水试验渗透系数k的公式为
(6)
规程[5]中假设压水试验段的定水头边界的半径R等于试段长度L,则式(6)可写为
(7)
式(7)即为规程中提供的岩体渗透系数的计算公式。利用该公式计算压水试验中岩体渗透系数时存在2个问题:①式(6)中定水头边界的半径R会因岩体渗透系数或储水系数的不同而不同,式(7)中人为假定R等于试段长度L显然会造成较大误差;②在一般压水试验的历时范围内,注入流量往往难以达到绝对的稳定,在稳定流计算中往往取最终流量值当作稳定流量进行计算,这种计算方法忽略了注入流量达到稳定之前的大量数据,存在较大的计算误差。因此将压水试验过程当作非稳定流来进行计算是合理的。
4 基于非稳定流假设的渗透系数计算方法
对压水试验过程进行非稳定流计算,沿用上述稳定流计算中的基本假设,根据地下水流动轴对称微分方程可得
(8)
式中:a为压力传导系数(m2/s);t为压水作用时间(s)。
另外有边界条件:①压水开始前(即初始阶段)水头面为水平;②压水试验段岩层侧向无穷远处压力水头为原始水头;③压水开始后试验段中水压力恒定。上述3种边界条件分别对应以下3式:
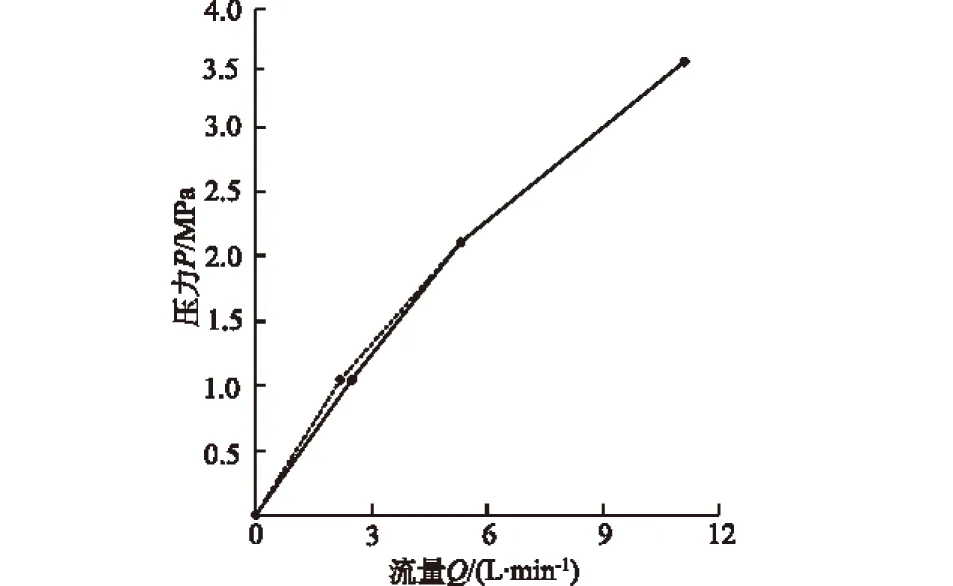
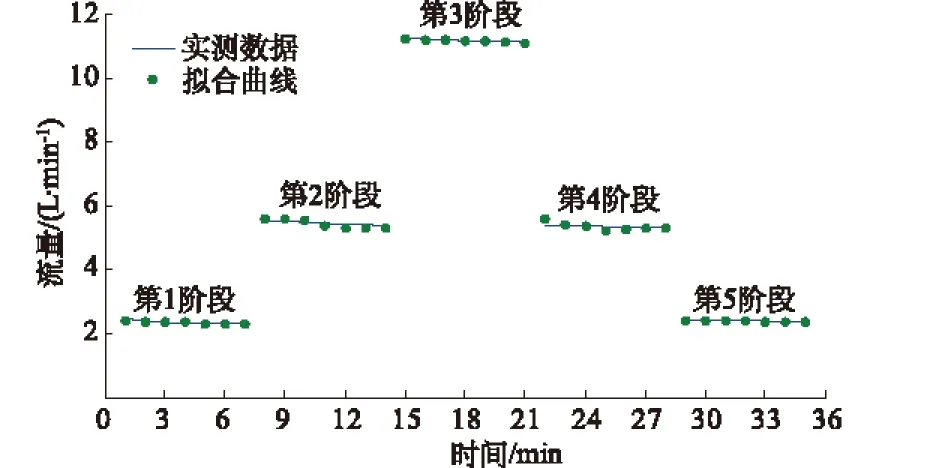
H(r,0)=0 ,rw (9) H(∞,t)=0 ,t>0; (10) H(rw,t)=Pw(常数) ,t>0 。 (11) 采用拉氏变换,并代入初始条件式(10),式(11),对式(8)进行求解得 H= (12) 根据达西定律,含水层任一断面的过水流量为 (13) 当r=rw时,压水试验段的注入流量可表示为 (14) 令 则式(14)可写为 (15) 式(15)即为压水注入流量Q与时间t的关系函数。根据式(15),利用压水实测资料Qi,ti(i=0,1,2,…,n),采用最小二乘法求得相应的压力传导系数a和渗透系数k。设M为a和k的函数: (16) 则上述问题转变为求函数M(a,k)在定义域上的极小值,解下列偏微分方程组可得参数a,k: (17) 用Matlab软件采用数值方法编程求解,即可求出压力传导系数a和渗透系数k。 镜屏一级水电站位于四川省凉山彝族自治州盐源县和木里县境内的雅砻江干流上,是雅砻江干流下游河段水电规划梯级开发的龙头电站。为评价大坝帷幕灌浆效果,需对帷幕灌浆进行压水试验。本文列举其中2例压水计算实例。 锦屏右岸帷幕灌浆某检查孔压水试验,取其中第一阶段压水试验数据进行一阶段压水计算。试验压力P=1.06 MPa,分别采用稳定流和非稳定流方法对压水数据进行计算并求得相关水文地质参数见表1;Q-t拟合曲线见图2。 图2 锦屏某灌浆检查孔一阶段压水试验结果与拟合曲线 从表1中可看出,采用非稳定流计算的渗透系数k要远远小于稳定流计算值。压水试验一般持续时间较短,在连续5次流量观测中,最大值与最小值之差小于最终值的10%或最大值与最小值之差小于1 L/min时,即结束该试验段压水,并取最终值作为稳定流计算值。但实际上,在该条件下水流还远远未达到真正的稳定流状态(若进一步延长试验时间,其流量还会继续降低),因此采用稳定流计算势必会导致计算值较真实值偏大。而采用非稳定流计算则是采用了全部的试验数据进行拟合求参。 表1 锦屏某灌浆检测孔一阶段压水试验水文地质参数 常规压水试验通常采用3级压力5个阶段进行压水,以锦屏右岸帷幕灌浆压水试验某试段为例。该段试验采用标准的五点法进行压水,第1、第5阶段压力为1.05 MPa,第2、第4阶段压力为2.11 MPa,第3阶段压力为3.51 MPa,其P-Q曲线见图3。 图3 锦屏某灌浆检查孔压水试验P-Q曲线 分别采用稳定流及非稳定流方法计算该试验段各级压力下的水文地质参数见表2,计算时应注意各级压力下时间t与流量Q之间的对应关系。Q-t拟合曲线见图4。 该压水试验段P-Q曲线类型属于扩张型,说明该试验段在压力作用下,裂隙状态发生了变化,岩体渗透性增大,但这种变化是暂时性的、可逆的。随着试验压力下降,裂隙又恢复了原来的状态,呈现出弹性扩张的性质。从表2中可看出,无论是采用稳定流还是非稳定率计算,其渗透系数k均能反映出上述变化规律。另外在非稳定流计算中,单位储水系数μs在不断增大。这是因为单位储水系数的定义为μs=γnβ+γα,其中γnβ表示在单位孔隙介质中,当水头变化一个单位时,由于水的膨胀而释放的水量,这部分一般为定值;而γα表示在单位孔隙介质中,当水头变化一个单位时,由于孔隙介质受压缩而释放的水量。那么在实际压水过程中,随着压水时长的增加,试验段周围的岩体在水压力作用下孔隙会逐渐增大,因此导致单位储水系数μs的增大。 表2 锦屏某灌浆检查孔五点法压水试验水文地质参数 图4 锦屏某灌浆检查孔五点法压水试验结果与拟合曲线 本文在均质条件下推导了压水试验中稳定流和非稳定流状态下的渗透系数计算公式,得到以下结论: (1) 对于不同孔径的钻孔,其压水试验吕荣值不具备可比较性,需将其进行标准化处理。 (2) 对于短时压水试验,注入流量往往难以达到绝对的稳定,若仅取最终流量值作为稳定流量进行计算,而忽略注入流量随时间变化的大量数据,将导致计算结果存在较大的误差。 (3) 对于常规五点法压水,稳定流和非稳定流计算均能正确反映渗透系数与P-Q曲线类型之间的对应关系,但非稳定流计算还体现了单位储水系数与压水时长之间的对应关系。 参考文献: [1] WAY S C,MCKEE C R.In-situ Determination of Three-dimensional Aquifer Permabilities[J].Groundwater, 1982, 20(5): 594-603. [2] BARKER J A.A Generalized Radial-flow Model for Pumping Test in Fractured Rock[J].Water Resources Research, 1988, 24(4): 1796-1804. [3] DERSHOWITZ W S,DOE T W.Analysis of Heterogeneously Connected Rock Masses by Forward Modeling of Fractional Dimension Flow Behavior[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(3/4): 652-663. [4] 张桢武,李兴成,徐光详.利用定压力非稳定流压水试验求水文地质参数[J].岩石力学与工程学报, 2004,23(15):2543-2546.(ZHANG Zhen-wu, LI Xing-cheng, XU Guang-xiang.Determination of Hydrogeological Parameters by Water Pressure Test of Steady-Pressure and Non-stationary Flow[J].Chinese Journal of Rock Mechanics and Engineering,2004, 23(15):2543-2546.(in Chinese)) [5] DL/T 5331—2005,水电水利工程钻孔压水试验规程[S].北京:中国电力出版社,2005.(DL/T 5331—2005,Code of Water Pressure Test in Borehole for Hydropower and Water Resources Engineering[S].Beijing:China Electric Power Press, 2005.(in Chinese))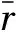

5 工程实例
5.1 一阶段压水计算实例


5.2 五点法压水计算实例

6 结 论
