基于最大-最小贴近度和诱导有序加权算子的风电功率短期预测模型

乔 梁1，张 露2，许 懿1，梁 伟1，孙 露3，卢继平2



基于最大-最小贴近度和诱导有序加权算子的风电功率短期预测模型

乔 梁，张 露，许 懿，梁 伟，孙 露，卢继平

(1.重庆电力调度控制中心，重庆 400000；2.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆 400044；3.重庆电力设计院系统处，重庆 401120)

为了提高风电功率短期预测精度，将最大-最小贴近度和诱导有序加权算子相结合，提出了一种新的组合模型。根据诱导有序加权算子的不同，可形成不同的组合模型，即IOWA组合模型、IOWHA组合模型和IOWGA组合模型。由于预测期的实际值未知，各单项预测模型的诱导值无法提前预知，不能直接利用该方法进行预测。利用各单项模型建立不同组合模型，选择精度较高的组合模型，用其预测值代替实际值计算诱导值，可以解决预测期诱导值的计算问题。两个不同风电场的仿真结果表明：IOWGA组合模型比某些单项模型和其他组合模型的预测精度还低，预测效果并未得到改善；IOWA组合模型和IOWHA组合模型的各项误差指标都小于单项模型和其他组合模型，预测精度都得到提高，但IOWHA组合模型的各项预测评价指标都最好，预测精度更高，将它的预测值作为风电功率最终预测值，能提高风电功率预测精度。

风电功率；最大-最小贴近度；IOWA组合模型；IOWHA组合模型；IOWGA组合模型

0 引言

随着风力发电技术的不断发展，风电在电力需求中所占比例越来越大。风电功率具有波动性和间歇性特点，因此大量风电场并网会影响电网的安全稳定运行。对风电功率进行准确预测可以增加风电接入容量、提高电力系统运行安全性与经济性。

目前，常用的风电功率预测方法主要有时间序列法、卡尔曼滤波法、灰色预测法、空间相关法、神经网络法、小波分析、支持向量机等。

以上每种方法都各有优劣和不同的适用场合，没有任何一种方法在任何情况都有较好的预测精度。因此采用组合预测方法对风电功率进行预测，充分利用各种单一预测模型的有效信息，可以提高风电场功率预测的精度。组合预测方法根据加权平均形式的不同分为加权算数平均（WA）、加权调和平均（WHA）和加权几何平均（WGA）。传统的组合预测方法中各单项预测方法的权系数在每时刻是固定不变的，然而同一单项预测方法在每个时刻的预测效果不尽相同，在某些点预测效果好，另些点预测效果较差，即传统组合预测方法没有考虑各个单项预测方法预测效果的动态性，对预测效果的改善并不明显。故本文引进诱导有序加权算子，三种不同的加权平均形式可形成三种诱导有序加权算子，即诱导有序加权算数平均算子（IOWA）,诱导有序加权调和平均算子（IOWHA）和诱导有序加权几何平均算子（IOWGA）。基于诱导有序加权算子建立的组合模型是根据各单项预测方法在每时刻的预测精度高低顺序赋值的，从而克服了传统组合模型的缺陷。

建立组合预测方法的优化准则有很多，大部分文献研究的是以某一误差指标最小建立组合模型，相关性指标作为优化准则的研究也越来越多，本文采用相关性指标最大-最小贴近度作为组合预测的优化准则，它能反应组合预测值和实际值的接近程度，用它作为优化准则具有可行性。

诱导有序加权算子需要对预测精度（诱导值）排序，但预测期实际值未知，诱导值排序无法提前知道。本文采用单项预测模型建立的一些组合模型中预测精度较高者的预测值作为标准，计算各单项

模型的诱导值，进而得到诱导值排序。

本文首先利用灰色预测法、时间序列法、BP神经网络法和SVM法对风电功率进行预测；然后利用各单项预测模型建立不同的组合模型，选择出精度较高的组合模型，并用其预测值与各单项预测值得到诱导值并对诱导值进行排序；接着以最大—最小贴近度最大为优化准则，分别建立基于IOWA、IOWHA和IOWGA的三种组合模型；最后，选择各项预测指标都较好的组合模型的预测值作为最终风电功率预测值。

1基本概念

1.1三种诱导有序加权算子

1.2最大-最小贴近度

2 基于最大-最小贴近度和诱导有序加权算子的组合模型

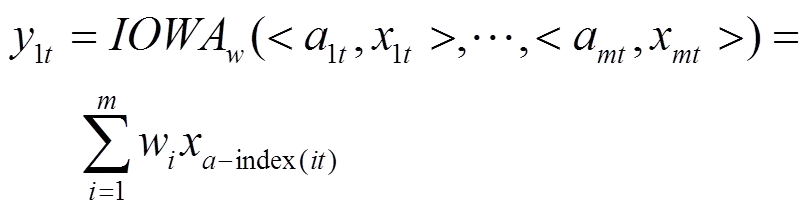
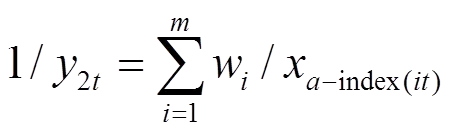
(12)

(13)

（14）

(15)

(16)

3 改进的组合预测模型

求各单项预测模型的预测精度时，需要知道实际风电功率值，但由于预测期的实际值未知，各单项预测模型的诱导值无法提前得知，故本文选择等权重组合模型、方差倒数法组合模型、熵值法组合模型和误差平方和最小组合模型中预测精度较高的组合模型，将它的预测值代替实际值进行诱导值的计算。

改进的组合模型只是在求得各单项预测模型的诱导值时采用较高精度组合模型，但在求IOWA组合模型、IOWHA组合模型和IOWGA组合模型时，仍以风电功率实际序列求得各模型的权系数。故改进的组合模型只是对各单项预测模型的诱导值计算进行了改进，其他过程与第2节相同，这里不再介绍。

4 算例分析

本文以云南某风电场2月1日至2月11日的风电功率数据为实验数据，数据的采样间隔为15 min，原始数据见图1。

图1原始风电功率数据

4.1预测评价指标

本文采用常用的预测评价指标来评价预测模型的预测效果，即平均相对误差（MRE）、平均绝对误差（MAE）、均方根误差（RMSE）和相关系数（CC）。它们的计算式如下：

4.2单项预测模型的预测效果

本文选择常用的四种风电功率预测方法，即灰色预测法（GM）、时间序列法（ARIMA）、BP神经网络法和支持向量机方法（SVM）。

在构建时间序列ARIMA模型、BP神经网络模型和SVM模型时，需要的建模数据较多，而GM方法适用于处理小样本预测，即所需建模数据较少。为了避免建模数据量带来的影响，对于ARIMA、BP和SVM方法，选择2月1日至2月10日的960个风电功率数据作为训练数据进行模型的建立，2月11日的96个风电功率数据作为测试数进行模型的预测。其中在构建BP神经网络模型和SVM模型的训练样本时，采用相空间重构的方法，一方面能得到用于建模的训练样本，另一方面也能得到模型的输入个数，从而解决了输入个数的确定问题。根据相空间重构的C-C方法，可得到原始数据的嵌入维数为5和延迟时间为21，因此BP神经网络模型和SVM模型的输入为，输出为，为训练样本，为测试样本。GM方法的建模数据个数取为与BP神经网络模型和SVM模型的输入个数相同，即为嵌入维数5，故利用956~960点的实际值预测961点的功率，然后用957~961点的实际值预测962点的功率，依次类推。

四种风电功率预测方法的预测效果和相对误差分别见图2、图3，各预测评价指标如表1所示。

表1各单项预测模型的预测结果分析

Table 1 Forecasting result analysis of each single forecasting model

分析图2得，各单项预测模型的预测曲线都能跟踪实际曲线的走势，但在风电功率变化比较快的区间，各单项预测模型的预测效果都较差，导致风电功率急剧变化的主要因素是风速变化的不稳定，故风速的不稳定变化影响风电功率的预测效果。

分析图3知，在大部分的预测时刻，各单项预测模型的预测相对误差都小于20%，只有小部分的预测点，相对误差较大。其中，GM模型和BP神经网络模型的相对误差波动较大，ARIMA和SVM模型的相对误差波动较小，但在每个时刻预测误差最小的点对应的模型并不完全相同，也就是说四种预测模型中的每种模型都有预测精度最高的时刻，说明各预测方法的预测效果在每个时刻不尽相同，在一些点预测效果最好，而在另一些点预测效果可能最差。

图2各单项预测模型的预测结果

图3 各单项预测模型预测的相对误差

Fig. 3 Relative errors of four single forecasting models

由表1可得，ARIMA和SVM模型的各项误差指标都较小，相关系数都较大，说明它们整体预测效果较好，其次是GM模型，BP神经网络的预测效果最差。

4.3各组合预测模型

利用各单项预测模型建立不同的组合模型，即等权重组合模型、方差倒数法组合模型、熵值法组合模型和误差平方和最小组合模型。它们的预测效果见表2所示。

表2各组合模型的预测结果分析

Table 2 Forecasting result analysis of each combination model

分析表1和表2知，组合模型的各项指标都优于单项模型，预测精度都高于单项预测模型，说明组合模型能提高预测精度。其中，组合模型中误差平方和最小组合模型的各指标都较好，与实际值接近程度更高，将它的预测值作为标准计算单项预测模型的诱导值具有可行性。

4.4改进的组合模型的预测分析

利用各单项预测模型的预测值和误差平方和最小组合模型的预测值计算得到诱导值，建立基于最大—最小贴近度和诱导有序加权算子的改进组合预测模型，即改进的IOWA模型、改进的IOWHA模型和改进的IOWGA模型，为了叙述方便，将它们分别简称为：IOWA模型、IOWHA模型和IOWGA模型。各诱导有序加权算子组合模型的权系数如表3所示。

表3三种组合模型的权系数

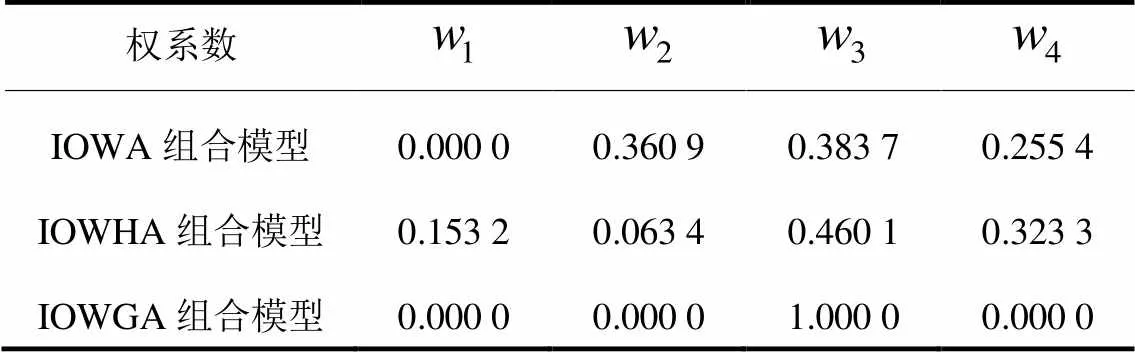
Table 3 Weight coefficient of three combination models

从表3中可知，IOWA组合模型的权系数和IOWGA组合模型的权系数、和为0，基于诱导有序加权算子的组合模型的权系数为0和传统组合模型的权系数为0的实际含义不同，若传统组合模型的某个权系数为0表示该单项预测方法在组合模型中是冗余方法，不提供任何有效的预测信息，而基于诱导有序加权算子的组合模型对各单项预测值根据诱导值由大到小的顺序进行对应的排序，它的某个权系数为0不能说明对应的单项预测方法不提供有效信息。

根据各组合模型的权系数和排序后的各单项预测值得到了三种组合模型，其预测效果如图4，预测评价指标如表4所示。

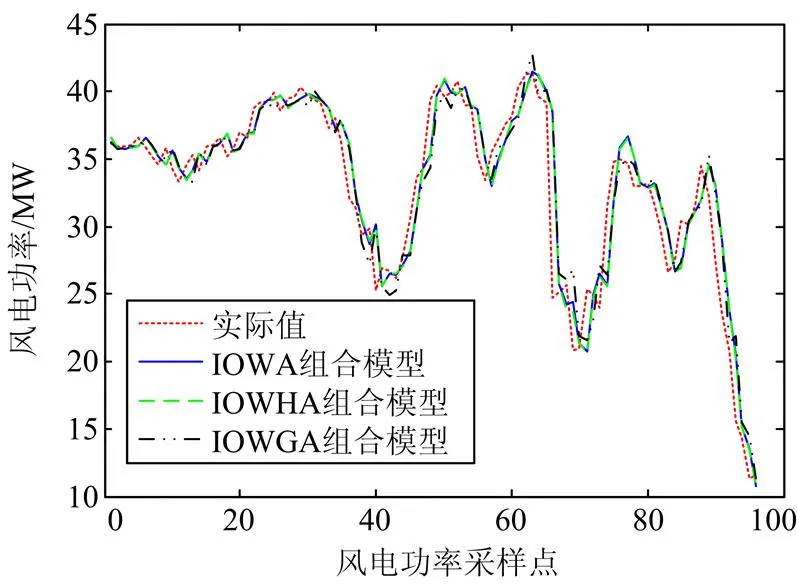
图4三种组合预测模型的预测结果

Table 4 Forecasting result analysis of three combination forecasting models

分析表1、表2和表4知，IOWA组合模型和IOWHA组合模型的各项预测评价指标都比各单项预测模型和其他组合模型好，而IOWGA组合模型的预测效果比某些单项预测模型和其他组合模型还差，说明以最大—最小贴近度为优化准则建立的IOWGA组合模型的预测精度并未得到提高。由表4得，IOWHA组合模型的各误差指标最小，相关系数最大，因此选择它为最终的预测值。

为检验以最大—最小贴近度为优化准则建立的IOWHA组合模型为最优模型，选择另一风电场的数据进行建模和预测，数据的采样间隔也为15 min，其原始数据如图5，该风电场数据变化具有一定周期性，波动性不大。限于篇幅，本文只列出了各单项预测方法、各组合预测法和三种诱导有序加权算子的组合模型的预测效果评价表5。

分析表5可知，以最大-最小贴近度为优化准则建立组合模型时，IOWA组合模型和IOWHA组合模型的预测精度都得到提高，其中IOWHA组合模型的预测效果更好；而IOWGA组合模型的预测精度比单项模型ARIMA、SVM和其他组合模型低，预测效果并未得到改善。此风电场的预测模型所得结论与前面云南风电场相似。因此以贴近度为优化准则建立的IOWHA组合模型为最优模型。

图5另一风电场的风电功率原始数据

5 结论

1）利用各单项预测模型的较高精度的组合模型预测值代替实际值计算诱导值，可以解决预测期实际值未知，因而诱导值排序无法提前预知的问题；同时较高精度的组合预测值与实际值较相近，将它的预测值作为标准计算单项预测模型的诱导值具有可行性。

表5各预测模型的预测结果分析

Table 5 Forecasting result analysis of each forecasting model

2）最大-最小贴近度是一种相关性指标，其能反应组合预测值与实际值的接近程度。将它作为优化准则具有可行性。

3）根据组合加权形式不同，本文建立了三种诱导有序加权算子的组合模型，并用两个风电场进行了实例分析，结果表明：以贴近度为优化准则建立组合模型时，改进的IOWGA组合模型的预测精度并未提高，而改进的IOWA组合模型和改进的IOWHA组合模型的预测效果都得到改善，但改进的IOWHA组合模型的各项预测评价指标都最好，预测精度更高，具有较好的预测能力，能有效提高风电功率预测精度。基于最大-最小贴近度的改进的IOWHA组合模型对于解决实际工程问题具有很好的应用价值。

[1] 王丽婕, 廖晓钟, 高阳, 等. 风电场发电功率的建模和预测研究综述[[J]. 电力系统保护与控制, 2009, 37(13): 118-121.

WANG Li-jie, LIAO Xiao-zhong, GAO Yang, et al. Summarization of modeling and prediction of wind power generation[J]. Power System Protection and Control, 2009, 37(13): 118-121.

[2] 冯双磊, 王伟胜, 刘纯, 等. 风电场功率预测物理方法研究[J]. 中国电机工程学报, 2010, 30(2): 1-6.

FENG Shuang-lei, WANG Wei-sheng, LIU Chun, et al. Study on the physical approach to wind power prediction[J]. Proceedings of the CSEE, 2010, 30(2): 1-6.

[3] TORRES J L, GARCIA A, DE BLAS M, et al. Forecast of hourly averages wind speed with arma models in Navarre (spain)[J]. Solar Energy, 2005, 79(1): 65-77.

[4] 姜婷, 周孝华, 董耀武. 基于Markov机制转换模型的我国股市周期波动状态研究[J]. 系统工程理论与实践, 2013, 33(8): 1934-1939.

JIANG Ting, ZHOU Xiao-hua, DONG Yao-wu. Stock market cycle fluctuation in China: Markov regime switching model[J]. Systems Engineering Theory & Practice, 2013, 33(8): 1934-1939.

[5] 陈昊, 王玉荣. 基于随机波动模型的短期负荷预测[J]. 电力自动化设备, 2010, 30(11): 86-89.

CHEN Hao, WANG Yu-rong. Short-term load forecasting based on SV model[J]. Electric Power Automation Equipment, 2010, 30(11): 86-89.

[6] 方江晓. 短期风速和风电功率预测模型的研究[D]. 北京: 北京交通大学, 2011.

[7] 潘迪夫, 刘辉, 李燕飞. 风电场风速短期多步预测改进算法[J]. 中国电机工程学报, 2008, 28(26): 87-91.

PAN Di-fu, LIU Hui, LI Yan-fei. Optimization algorithm of short-term multi-step wind speed forecast[J]. Proceedings of the CSEE, 2008, 28(26): 87-91.

[8] El-FOULY T H M, El-SAADANY E F, SALAMA M M A. Improved grey predictor rolling models for wind power prediction[J]. IEEE Proceedings on Generation, Transmission and Distribution, 2007, 154(6): 928-937.

[9] 李俊芳, 张步涵, 谢光龙, 等. 基于灰色模型的风速一风电功率预测研究[J]. 电力系统保护与控制, 2010, 38(19): 151-159.

LI Jun-fang, ZHANG Bu-han, XIE Guang-long, et al. Grey predictor models for wind speed-wind power prediction[J]. Power System Protection and Control, 2010, 38(19): 151-159.

[10] 党耀国, 刘思峰, 王正新, 等. 灰色预测与决策模型研究[M]. 北京: 科学出版社, 2009.

[11] 陈妮亚, 钱政, 孟晓风, 等. 基于空间相关法的风电场风速多步预测模型[J]. 电工技术学报, 2013, 28(5): 15-21.

CHEN Ni-ya, QIAN Zheng, MENG Xiao-feng, et al. Multi-step ahead wind speed forecasting model based on spatial correlation[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 15-21.

[12] BILLINTON R, CHEN H, GHAJAR R. A sequential simulation technique for adequacy evaluation of generating systems including wind energy[J]. IEEE Trans on Energy Conversion, 1996, 11(4): 728-734.

[13] 武小梅, 白银明, 文福拴. 基于RBF神经元网络的风电功率短期预测[J]. 电力系统保护与控制, 2011, 39(15): 80-83.

WU Xiao-mei, BAI Yin-ming, WEN Fu-shuan. Short-term wind power forecast based on the Radial Basis Function neural network[J]. Power System Protection and Control, 2010, 38(15): 80-83.

[14] BARBOUNIS T G, THEOCHARIS J B, ALEZIADIS M C, et al. Long-term wind speed and power forecasting using local recurrent neural network models[J]. Transactions on Energy Conversion, 2006, 21(1): 273-284.

[15] 韩力群. 人工神经网络教程[M]. 北京: 北京邮电大学出版, 2006.

[16] CAO Lei, LI Ran. Short-term wind speed forecasting model for wind farm based on wavelet decomposition[J]. IEEE Trans on DRPT, 2008: 2525-2529.

[17] 罗文, 王莉娜. 风场短期风速预测研究[J]. 电工技术学报, 2011, 26(7): 68-74.

LUO Wen, WANG Li-na. Short-term wind speed forecasting for wind farm[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 68-74.

[18] MOHANDES M A, HALAWANI T O, REHMAN S, et al. Support vector machines for wind speed prediction[J]. Renewable Energy, 2004, 29(6): 939-947.

[19] 夏冬, 吴俊勇, 贺电. 一种新型的风电功率预测综合模型[J]. 电工技术学报, 2011, 26(1): 262-266.

XIA Dong, WU Jun-yong, HE Dian. A novel combined model for wind power forecasting based on maximum entropy principle[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 262-266.

[20] 韩爽. 风电场功率短期预测方法研究[D]. 北京: 华北电力大学, 2008.

[21] 陈华友, 盛昭瀚. 一类基于IOWGA算子的组合预测新方法[J]. 管理工程学报, 2005, 19(4): 36-39.

CHEN Hua-you, SHENG Zhao-han. A kind of new combination forecasting method based on induced ordered weighted geometric averaging (IOWGA) operator[J]. Journal of Industrial Engineering, 2005, 19(4): 36-39.

[22] 夏立福, 李井春, 王洪海. 基于IOWA算子的组合预测模型研究及应用[J]. 测绘与空间地理信息, 2011, 34(1): 208-212.

XIA Li-fu, LI Jing-chun, WANG Hong-hai. Research and application on the method of deformation prediction based on IOWA operator[J]. Geomatics & Spatial Information Technology, 2011, 34(1): 208-212.

[23] 陈华友, 刘春林, 盛昭瀚. IOWHA算子及其在组合预测中的应用[J]. 中国管理科学, 2004, 12(5): 35-40.

CHEN Hua-you, LIU Chun-lin, SHENG Zhao-han. Induced ordered weighted harmonic averaging (IOWHA) operator and its application to combination forecasting method[J]. Chinese Journal of Management Science, 2004, 12(5): 35-40.

[24] 金飞飞, 陈华友, 周礼刚. 基于最大一最小贴近度的IOWA算子最优组合预测模型[J]. 数学的实践与认识, 2013, 43(7): 110-116.

JIN Fei-fei, CHEN Hua-you, ZHOU Li-gang. The optimal combination forecasting model based on the maximum-minimum approach degree and induced ordered weighted averaging operator[J]. Mathematics in Practice and Theory, 2013, 43(7): 110-116.

[25] 徐曼, 乔颖, 鲁宗相. 短期风电功率预测误差综合评价方法[J]. 电力系统自动化, 2011, 35(12): 20-26.

XU Man, QIAO Ying, LU Zong-xiang. A comprehensive error evaluation method for short-term wind power prediction[J]. Automation of Electric Power Systems, 2011, 35(12): 20-26.

[26] 韩敏. 混沌时间序列预测理论与方法[M]. 北京: 中国水利水电出版社, 2007.

Wind power short-term forecast model based on maximum-minimum approach degree and induced ordered weighted operator

QIAO Liang, ZHANG Lu, XU Yi, LIANG Wei, SUN Lu, LU Ji-ping

(1. Chongqing Electric Power Dispatching Control Center, Chongqing 400000, China; 2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology (Chongqing University), Chongqing 400044, China; 3. Chongqing Electric Power Design Institute, Chongqing 401120, China)

In order to improve the accuracy of wind power short-term forecast, a kind of new combination forecasting model is proposed combining the maximum-minimum approach degree with induced ordered weighted operator. According to different induced ordered weighted operators, different combination forecasting models can be constructed, namely IOWA combination model, IOWHA combination model and IOWGA combination model. Because real data are unknown in the forecast period and induced value of every single forecasting method can’t be calculated in advance, this method can not be used to predict directly. Forecasting value of the highest accuracy combination forecasting model selected from different combination models built by single forecasting models instead of real data can solve the induced value calculation. Simulation results of two different wind power farms show that compared with some single forecasting models and another combination models, the forecast precision of IOWGA combination model is lower and predictive effect isn’t improved; forecasting error indexs of IOWA combination model and IOWHA combination model are all lower and forecast precision of those is higher, moreover, predictive effect of IOWHA combination model is better than IOWA combination model, therefore, taking forecast value of IOWHA combination model as final prediction result can effectively improve the prediction accuracy of wind power. This work is supported by Independent Research Project of State Key Laboratory of Power Transmission Equipment & System Security and New Technology (No. 2007DA10512712205).

wind power forecast; maximum-minimum approach degree; IOWA combination model; IOWHA combination model; IOWGA combination model

TM614

A

1674-3415(2014)19-0114-08

2013-12-26；

2014-03-05

乔 梁(1981－)，男，硕士，工程师，研究方向为电力系统继电保护与运行；E-mail: xiaoguei2003@163.com

张 露(1990－)，女，通信作者，硕士研究生，研究方向为风电功率预测与控制。

输配电装备及系统安全与新技术国家重点实验室自主研究项目(2007DA10512712205)