无线网络中节点移动性对病毒传播行为的影响
2014-08-15刘子超孙世温王莉王娟夏承遗
刘子超,孙世温,王莉,王娟,夏承遗
(1.天津理工大学 天津市智能计算与软件新技术重点实验室,天津 300384; 2.天津理工大学 教育部计算机视觉与系统重点实验室,天津 300384)
计算机的使用已经从原有的科学计算逐渐走入人们的生产、生活中[1]. 与此同时,对于计算机的信息安全的研究也越来越受到人们的重视.在蠕虫和病毒传播模型的研究中,主要是利用传统的生物工程中的传染病传播模型的研究成果,结合计算机网络中的病毒的特点,形成适于描述计算机病毒传播的模型.目前研究广泛的传播模型包括SI(susceptible-infectious),SIS(susceptible-infectious-susceptible)和SIR(susceptible-infectious-refractory)3个病毒传播模型. 在SI模型中,网络中的节点被划分为易感节点(S)和感染节点(I)2类,感染节点为传染源,以一定的概率将病毒传染给易感节点,易感节点一旦被感染,就会变成新的传染源,并且传染节点不能被治愈[2-3]. 在此模型的基础上,SIS模型中考虑了感染节点被治愈的情况,即感染节点可以通过一定概率转变为易感节点[4-5]. 在SIS模型的基础上,SIR模型中引入了“免疫状态”,即网络节点以一定的概率进入免疫状态从而不会被感染,也不会感染其他节点[6-7].
随着无线网络应用的不断扩展,以及智能手机在人们生活中不断普及,无线网络中信息安全已经成为无线网络技术发展和应用的一个瓶颈和关键问题[8]. 许多研究者都在着手于研究网络拓扑的特点对病毒传播过程的影响,其中有影响的研究成果包括:Kephart等[9]率先扩展了传统流行病模型的研究,考虑主机之间的本地交互特性,将传播模型引入到非同质网络包括随机图、二维网格和树形等级网络等. 在病毒和蠕虫传播模型的研究领域,Staniford等[10]提出随机常数传播模型(random constant spread model,RCS)来模拟红色代码蠕虫的爆发过程. Zou等[11]在考虑人为对抗措施以及由蠕虫引起的网络拥塞等因素影响基础上提出的“双因素”蠕虫模型更能模拟网络蠕虫的传播状态.为了更好地分析传播受限制的计算机病毒,Serazzi等[12]考虑了节点之间带宽的因素,在RCS模型的基础上提出了一种基于Internet自治层结构的新模型——间隔模型. Zou等[13]对电子邮件病毒传播模型进行了相应的分析. Chen等[14]使用时空随机过程描述了恶意软件在任意网络拓扑下的统计依赖性. 本文将传统的SIS模型应用到无线网络中病毒传播行为的分析与建模中,着重讨论以蓝牙网络为代表的一类无线网络上病毒传播特性,发现网络中节点移动性能够显著影响病毒的传播行为,为深入研究无线网络上的病毒传播行为提供了一些有益的探索,也为无线通信网络上病毒的预警和控制提供一定的理论基础.
1 系统模型
1.1 系统结构建模
图1 蓝牙网络拓扑Fig.1 Topology of the Blue-tooth network
以蓝牙网络为代表的无线网络的一个显著特点就是网络节点的移动造成的网络拓扑的不断变化,基于这一特点分析现有的病毒模型的研究相关内容,不难发现一个共同的特点,这些模型都是在假定网络节点的链接是固定的,即病毒传播过程中网络拓扑不会发生变化,但这与无线网络的实际特点存在着一定的偏差,因此,在研究新型病毒模型,引入网络节点移动使网络拓扑发生变化,是无线网络病毒模型传播的一个重要的发展方向. 本文以蓝牙网络为载体,研究分析节点的移动性对病毒传播的影响,实验网络模拟采用均匀随机网络部署,初始化的网络部署采用类似于蜂窝网络的网络拓扑,在网络中每个节点周围都存在着6个与之相邻的网络节点,且该节点到达周围节点的距离是相同的,节点之间的连通性被认为是全连通,但是根据无线网络的实际特点,实验假定节点的信号覆盖范围是一个圆形区域,并且不同节点的信号覆盖外围是不相同的,在本文的实验模拟过程中使用随机函数随机设定节点的信号覆盖在10~15 M的圆形区域内,实验网络部署拓扑图如图1所示.
在仿真实验中,在上述初始化类似于蜂窝网络的网络结构模型的基础上,使网络中的节点按照指定的方式在指定的网络区域内移动,实验过程中,设定网络的节点在特点的速度范围内朝任意方向运动,为了保证节点不离开实验区域,实验过程中使用“越界反转”的方法[12],将节点控制在指定的区域,从而保证实验过程中节点的总数不变.
1.2 病毒传播模型
近年来,无线网络技术与产品得到快速发展,特别是以智能手机为基点的移动网络逐步走进人们的生活中,对于网络中的恶意程序以及病毒的防范还处于初步阶段,对于这种网络病毒的防护还比较脆弱.因此,在网络病毒的传播过程中,当节点与已感染节点接触时,易感节点会以一定的概率变为感染节点,这个阶段可以视为病毒传播的感染过程,然而,当网络中的节点被感染之后,由于杀毒软件等人为手段的介入,网络中的感染节点会以一定的概率回到易感状态. 本文采用经典的病毒传播模型SIS,该病毒模型的主要特点就是节点在易感状态与感染状态2种状态之间能以一定的概率相互转换,这符合现在无线网络中病毒传播过程的实际特点
1.3 网络中节点的移动性模型
对无线网络的移动特点的研究前任已做了很多研究工作,本文中的移动性模型采用经典的随机游走模型RWM(random walk model),该模型的原型是物理学中著名的布朗运动模型,该模型可以较好地模拟某些应用场景中节点的极端不规则的移动方式.在这个模型中,节点从当前的位置随机选择一个速率和方向,运动固定的时间t或固定距离d后到达一个新的位置,然后重复上述过程直至模拟仿真结束.其中,速率v和方向θ分别服从区间[Vmin,Vmax]和[0,2π]上的均匀分布.分别用v∈U[Vmin,Vmax],θ∈U[0,2π]来表示.
如果节点到达了仿真区域的边界,节点就会从边界脱离,然后从另外一个对称的方向进入仿真区域,在该运动模型中,节点的总数保持不变,节点在指定的模拟范围不停的移动直至模拟结束.
2 数值仿真
由于上述的模型是基于平均场近似条件下得到的,必须通过大量的数值仿真来验证结果的有效性,并对结果进行分析.
2.1 仿真算法
1)首先按照系统结构模型的结构,将网络中的节点平均部署在上述类似于蜂窝网络状的网络拓扑结构上,并保存边界条件.
2)在1)中已经部署的网络拓扑节点上,随机部署若干感染节点,并且尽量的做到感染节点不聚集在一起.
3)对网络中所有节点做移动操作,包括网络节点的越界转化,网络中的节点移动的方向是完全随机的,并且在一个时间步中网络中的节点移动的距离也是在一定的范围内随机的.
4)对3)中移动后的节点进行SIS感染迭代处理,模拟病毒传播的实际过程.
5)检测仿真是否结束,否则跳转3)继续.
2.2 仿真结果
依照上述的仿真算法,本文不仅分析不同的感染率、治愈率等对SIS传染过程的影响,而且讨论了网络中节点的移动速率和移动角度对病毒传播行为的影响.文中所有实验结果都是经过100次仿真后求得的平均结果.
初始时感染节点所占的比例为0.05,感染节点被随机的部署在整个模拟区域中,其余节点全部处于易感状态,本文所有的实验都是在实验节点数N=10 000的基础上进行的,后文中不再进行赘述.
图2中描述的曲线为病毒在带有节点移动性的类似于蜂窝状网络拓扑条件下,按照SIS传播模型传播,当病毒的感染率大于临界值且治愈率和节点移动速度一定时,不同感染率对病毒传播过程中感染节点所占比例的影响.其中感染率被分别设定为β=0.2,0.3,0.35,而治愈率为γ=0.25,节点移动时,速度V=10 m/s.从图2中可以看出,随着网络病毒的感染率的提高,网络中病毒传播的速度上升,并且稳态时感染节点所占的比例增大,并且通过对比无移动条件下相同感染率和免疫率时的实验曲线发现,节点的移动性加快了网络病毒的传播,并使得稳态时网络中感染节点所占的比例增大了.因此,控制节点移动与降低网络病毒的感染率是控制网络病毒传播的关键手段.
图3中描述的曲线为病毒在带有节点移动性的类似于蜂窝状网络拓扑条件下,按照SIS传播模型传播,当病毒的感染率大于临界值且治愈率和节点移动速度一定时,不同治愈率对病毒传播过程中感染节点所占比例的影响.其中治愈率被分别设定为γ=0.1,0.25,0.3,而感染率为β=0.3,节点移动时,速度V=10m/s.设定从图中可以看出,随着网络病毒的治愈率的提高,网络中病毒传播的速度下降,并且稳态时感染节点所占的比例下降.因此,提高对病毒的治愈率是控制网络病毒传播的关键手段.
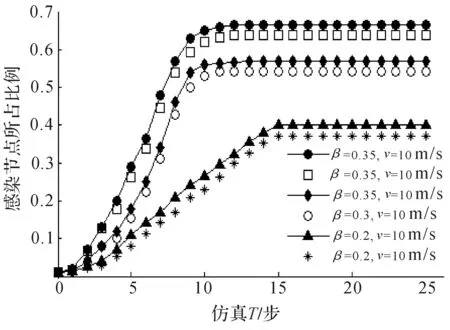
图2 在γ=0.25时,感染率β和移动性对病毒传播过程的影响Fig.2 Effect of infection rates β and mobility on the process of the virus propagation at γ=0.25
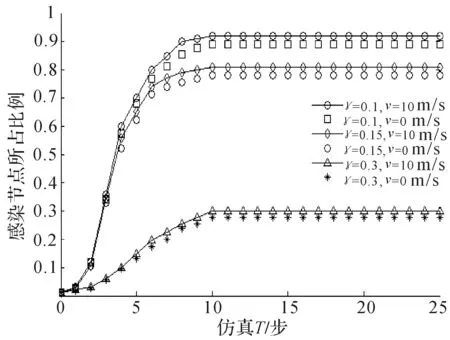
图3 在β=0.3时,治愈率γ和移动性对病毒传播过程的影响Fig.3 Effect of remove rates β and mobility on the process of the virus propagation at β=0.3
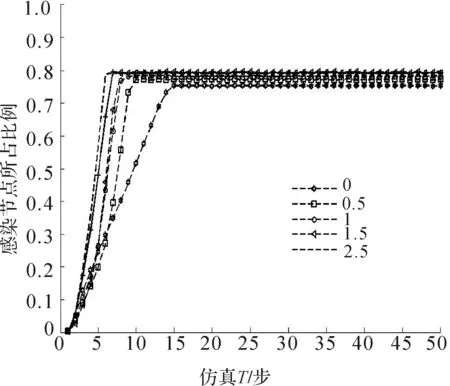
图4 不同的移动速度对病毒传播的影响Fig.4 Effect of different mobile speeds on the spreading of the viruses
图4中所示的曲线是按照上面的仿真算法得到的数据结果中感染节点所占的比例曲线,在实验中,假设模型中节点的感染率β=0.3,感染节点恢复率γ=0.2,通过100次重复的仿真实验得到数据求平均后得到如图4所示数据曲线,由图中的曲线可以发现依照SIS病毒模型的特点,仿真中感染的节点在网络中所占的比例经过一段时间的不同上升过程,最终达到一个相同的平衡状态,虽然这种状态时节点所占的比例各不相同,但是确是相同的稳定的状态,通过对图4的分析可以得到,随着节点移动的速度加快,病毒在网络中的感染速度加快,并且当网络最终达到平衡态时,网络中感染节点所占的比例也越大.
从图4中可以看出,在仿真的开始阶段,由于感染节点在网络中所占的比例较小,节点的移动速度对网络中病毒的传播影响不大,随着网络中感染节点的增加,网络中节点的移动速度越大,网络中的病毒传播的越快,并且所达到的感染节点所占比例的平衡值也越大.
3 结 论
将现有的SIS病毒传播模型引入没有固定拓扑的无线网络中,网络节点的信息交互是通过无线的信号覆盖来实现的,这种覆盖是在圆形区域内,更符合无线网络病毒研究的实际特点.通过上面的仿真可以看到移动网络中节点的移动速度是影响病毒传播行为的一个重要因素. 因此,通过制定有效的策略来控制网络中节点的移动速度,能够在一定程度上减慢网络中病毒的传播,提高网络中信息传播的安全性.
参 考 文 献:
[1] 文伟平, 卿斯汉, 蒋建春,等.网络蠕虫研究与进展[J].软件学报, 2004,15(8):1208-1219.
WEN Weiping,QING Sihan, JIANG Jianchun, et al. Research and development of internet worms [J]. Journal of Software, 2004, 15(8):1208-1219.
[2] 方义,夏承遗,刘子超,等. 闪烁小世界网络上疾病传播的动态行为研究 [J]. 复杂系统与复杂性科学,2011,8(3): 34-37.
FANG Yi, XIA Chengyi, LIU Zichao, et al. Dynamical behavior of disease spreading on blinking small-world networks [J]. Complex systems and complexity science, 2011, 8(3): 34-37.
[3] FUHRMAN KM, LAUKO I G, PINTER G A. Asymptotic behavior of an SI epidemic model with pulse removal [J]. Mathematical and Computer Modeling, 2004, 40(3): 371-386.
[4] ZHANG Xu, LIU Xianning. Backward bifurcation and global dynamics of an SIS epidemic model with general incidence rate and treatment [J]. Nonlinear Analysis: Real World Applications, 2009, 10: 565-575.
[5] SHI Hongjin, DUAN Zhishe, CHEN Guanron. An SIS model with infective medium on complex networks [J]. Physical A, 2008, 387: 2133-2144
[6] MANOJIT ROY, ROBERT D HOLT. Effects of predation on host-pathogen dynamics in SIR Models [J]. Theoretical Population Biology, 2008, 73(3): 319-331.
[7] 赵敬,方义,夏承遗. 考虑个体移动和局域控制的SIR传染模型 [J]. 智能系统学报,2011, 6(6): 515-519.
ZHAO Jing, FANG Yi, XIA Chengyi. A Susceptible-Infected-Removed model considering individual mobility and local control [J]. CAAI Transactions on Intelligent Systems. 2011, 6(6): 515-519.
[8] KLEINBERG J. The wireless epidemic [J]. Nature, 2007, 449: 287-288.
[9] KEPHART J O. Computers and Epidemiology [J]. IEEE Spectrum, 1993, 30: 20-26.
[10] STANIFORD S, PAXSON V, WEAVER N. How to own the Internet in your spare time [M]// BONEH D. Proceedings of the 11th USENIX Security Symposium.New York: ACM Press, 2002: 149-167.
[11] ZOU C C, GONG W B, TOWSLEY D. Code red worm propagation modeling and analysis [M] //ATLURI V. Proceedings of the 9th ACM Conference on Computer and Communications Security.New York: ACM Press, 2002: 138-147.
[12] SERAZZI G, ZANERO S. Computer virus propagation models [J]. Lecture Notes in Computer Science, 2004, 2965: 26-50.
[13] ZOU C C, TOWSLEY D, GONG W B. Email worm modeling and defense [M] // LUIJTEN R P.Proceedings of the 13th International Conference on Computer Communication and Networks, Chicago: IEEE Computer Society Press, 2004: 409-414.
[14] CHEN Zesheng, JI Chuanyi. Spatial-temporal modeling of malware propagation in networks [J]. IEEE Transactions on Neural Networks, 2005, 16(5): 1291-130
