BDS/GPS组合相对定位方法及精度分析

王世进，秘金钟，谷守周，祝会忠

(1. 中国地震局第一监测中心，天津 300180; 2. 中国测绘科学研究院，北京 100830; 3. 辽宁工程技术大学，辽宁 阜新 123000)

一、引 言

随着北斗卫星的快速组网，目前北斗卫星导航系统已经具备亚太地区的三维定位导航的能力。北斗系统的定位尤其是高精度定位的研究已经有了许多成果，但是基于BDS/GPS的双系统联合定位的实现细节讨论比较少，而且大都集中在精度的分析上[1-2]，算法介绍以及联合定位中的细节少有提及。本文从北斗系统和GPS的时间系统、坐标系统和卫星类型等不同点入手，介绍基于时空基准统一的双系统定位数学模型，探讨了不同卫星间的定权方法，并给出权比分配。然后从理论上对伪距双差和载波相位相对定位进行了阐述。

本文BDS/GPS实测数据是利用和芯星通BDS/GPS双频高精度接收机采集。在实测数据的处理中首先分析了北斗卫星的观测情况及位置精度衰减因子，然后对实测数据进行上述算法的计算，最后对定位结果进行了分析总结。定位结果表明，北斗的高精度定位结果已经和GPS相当，不仅验证了本文算法的有效性，也在一定程度上验证了北斗卫星导航系统的定位精度和可靠性。

二、BDS/GPS定位的时空基准统一

1. 坐标系统的统一

北斗卫星导航系统采用CGCS2000坐标系，GPS采用WGS-84坐标系，两者关于坐标系的原点、尺度、定向及定向演变的定义都相同的。两个坐标系的主要不同在于参考椭球的扁率f有微小的差异，而这种差异在当前的测量精度水平(坐标测量精度1 mm，重力测量精度1×10-8ms-2)中可以忽略，鉴于在坐标系定义和实现上的比较，可以认为在相同历元下CGCS2000和WGS-84在坐标系的实现精度范围内，两者的坐标是一致的[3]，本文的BDS/GPS定位程序中采用的是CGCS2000坐标系的参考椭球参数。

2. 时间系统的统一

BDST采用原子时，秒长和GPST相同，但是两者的起算点不一致，从而导致两者之间有一个常数差异。在RENIX3.X版本的导航文件中采用的是GPST，因此在进行定位时，需要转换观测值文件中北斗卫星的观测时间，转换关系如下

BDT=GPST-14

(1)

经过上述转换，解决了BDS/GPS定位中时空基准不同的问题，此外，北斗卫星中的卫星类型不同，含有MEO卫星、IGSO卫星和GEO卫星，前两种卫星位置计算和GPS卫星一样，GEO卫星位置的计算采用北斗ICD文件公布的算法实现[4]。

三、BDS/GPS定位算法

1. 数学模型

BDS/GPS伪距和相位的双差观测方程为

简化后的BDS/GPS载波相位相对定位的法方程的矩阵式为

式中

2. 定位算法过程

由于北斗系统和GPS都是全球导航定位系统且有等量级的精度水平，故北斗卫星和GPS卫星的观测值之间的权比为1∶1。北斗卫星星座是由3种不同类型的卫星组成的混合星座，即中高度圆轨道卫星(MEO)、倾斜地球同步轨道卫星(IGSO)和地球静止轨道卫星(GEO)。对于北斗系统内部的3种卫星的观测值之间应采用不同的权，GEO卫星属于高轨卫星，受太阳光压影响大，测距误差大约为11 m，而且只能区域定轨，导致其轨道精度较低，因此GEO卫星的观测值应采用较小的权；MEO卫星属于中轨卫星，受太阳光压影响小，测距误差大约为8 m，可以采用全球定轨的方式提高其轨道精度，因此MEO卫星的观测值应采用较大的权比；IGSO卫星的局部地区轨道精度高，虽然测距精度不如MEO卫星高，但是综合考虑可以采用和MEO卫星一样的权[6]。在观测方程中3种卫星观测值的权比为

EIGSO∶EMEO∶EGEO=2∶2∶1

(6)

伪距双差可以利用伪距双差方程结合上述权比，采用最小二乘法解算实测的BDS/GPS数据。

四、BDS/GPS相对定位的结果及精度分析

1. 观测数据的初步分析

本文采用的数据为和芯星通BDS/GPS双频接收机于河北临城采集的BDS/GPS短基线数据，基线长为9670 m, 观测时间为2012年12月14号，观测6487个历元。首先分析GPS、BDS卫星的个数(卫星高度截止角取15°)和PDOP值(位置精度衰减因子)，如图1所示。

图1 卫星个数及PDOP值

由图1(a)可以看出，观测到的北斗卫星个数要多于GPS卫星，这主要是由于在亚太地区可以观测到稳定个数的GEO卫星和IGSO卫星的结果，这样可以在一定程度上改善卫星的空间几何结构，提高定位精度，而且可进行定位的范围能大大增加。PDOP值代表位置精度衰减因子，值越小、越稳定位置精度越好，从图1(b)可以看出虽然北斗的卫星个数要多于GPS卫星，但是PDOP值有时没有GPS卫星的小，这说明北斗卫星的空间几何结构不如GPS卫星稳定，但是随着今后北斗MEO卫星的陆续补充，会大大改善卫星的空间几何结构，此外BDS/GPS的PDOP值要小于单个系统的值，而且稳定性好，因此可以预测双系统定位的精度要好于单个系统。

2. 伪距双差定位结果分析

分别采用BDS、GPS、BDS/GPS数据进行伪距双差定位解算，可得出东方向E、北方向N、天顶方向U3个坐标误差，如图2所示。

图2 伪距双差定位结果

图2是3种系统组合方式的定位结果图，从图中可以很直观地看出，BDS/GPS的坐标差比单个系统的要稳定。为了能定量地分析这3种组合方式的定位精度，由定位结果可以得到伪距双差定位绝对误差的均方根误差(RMS)，见表1。从表1中可以看出， GPS在N方向和U方向上的定位精度要优于北斗系统，而北斗在E方向上的精度优于GPS，这是由于北斗系统在东西方向上的卫星个数十分稳定，而整体的卫星空间几何结构不如GPS，因此导致整体精度不如GPS。BDS/GPS的定位结果在3个方向上的精度都优于单系统的精度，分析结果也验证了上述“双系统的定位精度要好于单个系统”的初步预测。

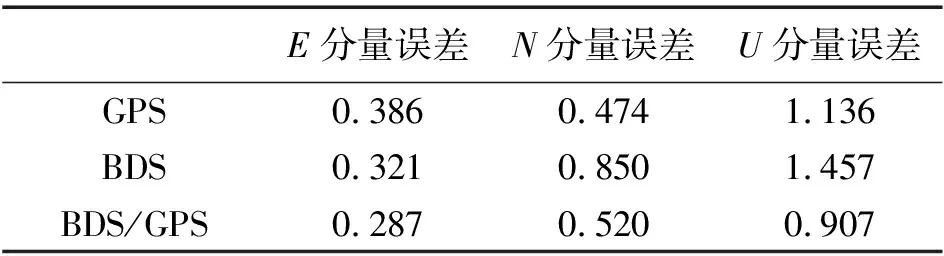
表1 伪距双差定位结果绝对误差RMS值 m

3. 载波相位动态相对定位结果分析

分别对BDS、GPS、BDS/GPS数据进行载波相位相对定位解算，可得出E、N、U3个方向的坐标误差，如图3所示。

图3 载波相位相对定位结果

图3是3种系统组合方式的高精度定位结果图，由定位结果可以得到载波相位相对定位绝对误差的均方根误差(RMS)，见表2。从图3和表2的结果来分析可以得到和伪距双差结果一样的结论。从定位结果来看，BDS/GPS高精度定位的稳定性和精度均有所提高。

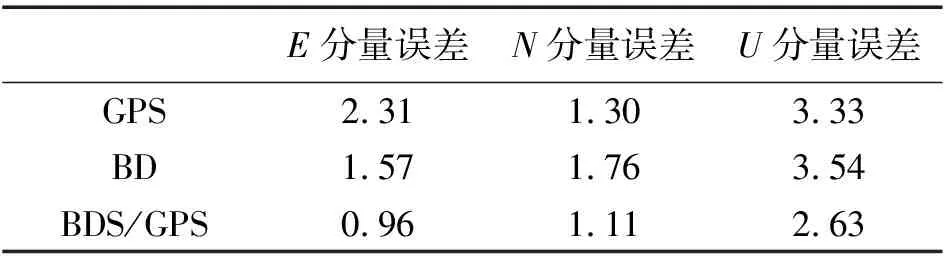
表2 载波相位相对定位结果绝对误差RMS值 cm

五、结束语

本文阐述了BDS/GPS定位的算法，并且结合北斗卫星导航系统的特点，详细介绍了联合定位的时空基准统一的内容，给出定位中的数学模型和各种观测值间的权比分配，利用本文算法处理了BDS/GPS实测数据，计算结果验证了本文算法的有效性。

由于北斗系统还在建设当中，卫星的分布不均匀，导致卫星的空间几何结构不如GPS，从定位结果来看，北斗系统的定位精度稍逊于GPS，但是可以预见，在北斗系统建设完成后，定位精度至少和GPS定位精度相当。

BDS/GPS的定位精度和稳定性要比单一系统优越，短基线的BDS和BDS/GPS的定位精度都可以达到厘米级。这说明目前北斗系统的高精度定位是可以实现的，而且多系统联合定位是提高定位精度的一种重要的手段，本文为GNSS定位提供了一定的参考。

参考文献：

[1] SHI C，ZHAO Q，HU Z，et al. Precise Relative Positioning Using Real Tracking Data from COMPASS GEO and IGSO Satellites[J]. GPS Solution, 2013,17(1):103-119.

[2] 高星伟，过静珺，程鹏飞，等．基于时空系统统一的北斗与GPS融合定位[J]．测绘学报，2012，41(5)：744-748．

[3] 党亚民,成英燕,薛树强．大地坐标系统及其应用[M].北京:测绘出版社,2010:154-157.

[4] 中国卫星导航系统管理办公室．北斗卫星导航系统空间信号接口控制文件公开服务信号B1I(1.0版)[EB/OL].2012-12-01[2013-03-01].http:∥www.beidou.gov.cn/.

[5] 霍夫曼-韦伦霍夫，利希特内格尔，瓦斯勒．全球卫星定位系统GPS，GLONASS，Galileo及其他系统[M]． 程鹏飞，蔡艳辉，文汉江，等，译．北京：测绘出版社，2008:146-178.

[6] 范龙，柴洪洲．北斗二代卫星导航系统定位精度分析方法研究[J].海洋测绘，2009,29(1):25-28.

[7] 何海波．高精度GPS动态测量及质量控制[D].郑州：信息工程大学，2002:42-56.

[8] 高为广，杨元喜，张双成．基于当前加速度模型的抗差自适应Kalman滤波[J]．测绘学报，2006，35(1)：15-18．

[9] 方荣新，施闯，魏娜，等．GPS数据质量控制中实时周跳探测研究[J]，武汉大学学报：信息科学版，2011，34(9):1094-1097.

[10] Teunissen P J G.The Least-Squares Ambiguity Decorrelation Adjustment:a Method for Fast GPS Integer Ambiguity Estimation[J].Journal of Geodesy,1995,70(1-2):65-82.