Gram多项式拟合在纸机横向定量测量数据去噪中的应用

连钰洋 汤 伟 胡连华 刘慧忠

(1.陕西科技大学电气与信息工程学院，陕西西安，710021；2.陕西科技大学轻工与能源学院，陕西西安，710021)

纸机生产过程中，定量作为评价纸张品质的最重要的指标之一非常重要。O型扫描架是横向定量控制系统传感器，用于测量纸张横向定量。由于工业现场存在干扰，测量值中含有噪声，这对施加控制十分不利。传统的去噪方法频率域低通滤波、滑动平均滤波、中值滤波具有一定的去噪效果，但已不适合更高质量的横向定量控制系统。本课题通过引入Gram多项式，利用最小二乘估计算法对横向定量测量数据进行滤波去噪。Matlab仿真结果表明，该方法具有较好的去噪效果。

1 Gram多项式

1.1 Gram多项式定义

对于函数系{Pj(x)}，在离散点集x(i)关于权函数w(x)，若有：

(1)

则称函数系{Pj(x)}是正交函数系。对于等间距的数据点，当w(x(i))=1时，离散正交多项式称为Gram多项式系(以下简称Gram多项式)[1]。

Beck和Arnold给出了计算均匀分布的N个测量点的正交多项式的递推方法。对每个多项式乘以一个标量，多项式系的正交性不受影响。多项式系的通式可以写作：

i=0,1,2,…,N-1

(2)

m是多项式的阶次。当cmN=1时，可以写作以下递推形式：

(3)

其中，P0(i)=1，P-1(i)=0。前3个多项式为：

(4)

它们常被称为离散的勒让德多项式(Legendre)，为了更直观地说明这一点，图1给出了Gram多项式和勒让德多项式通式的3次项，其他项与此类似。

图1 勒让德多项式与Gram多项式对比

由于要保证较好的离散正交性，当选取离散点个数较少时，Gram多项式和勒让德多项式有较大偏离，当离散点个数为500时，两者几乎重合。因此，随着离散点数增多，离散的Gram多项式不断接近勒让德多项式。

1.2 Gram多项式拟合

如图2所示，在整个横向定量控制系统中，去噪属于数据预处理。沿整个纸幅执行器(稀释水阀)个数众多，不同执行器间存在耦合，控制难度大。为了使控制系统能有较好的控制效果，去噪部分不希望引入新的干扰因素，所有数据要有相同权重，以防执行器紊乱。去噪前后离散点个数要保持不变，以便控制器保持输入维数相同。整个横幅的定量起伏变化较多，低次多项式拟合难以达到满意效果，往往要大于10次。最小二乘估计拟合涉及到矩阵求逆，如果基函数满足离散正交性将简化计算和工程实现，这就需要连续正交多项式合理离散化。前文提到，Gram多

图2 横向定量控制系统结构图

项式是对于等间距的数据点，权函数恒为1的离散正交多项式系，它是一种离散的勒让德多项式。通过适当变形将Gram多项式写为矩阵形式，可保证去噪前后信号点个数不变，同时它对不同离散点都有较好的离散正交性，对不同纸机及纸张类型均适用。因而，Gram多项式可以用于纸机横向定量测量数据的去噪，具体方法如下。

假设O型扫描架从纸幅一侧到另一侧扫描点个数为N，定义一个矩阵x0包含前m个正交多项式和N个离散点

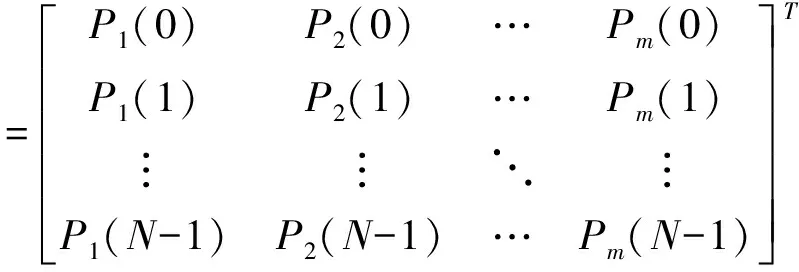
(5)

关于正交基函数系x0，扫描架测量的含噪定量y可以写作：

(6)

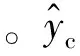
(7)

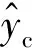
(9)

所以参数可以随需求添加又不影响已经算好的参数。最终，去噪后的定量为：

(10)

2 仿真分析

图3 含高斯噪声的定量测量数据去噪

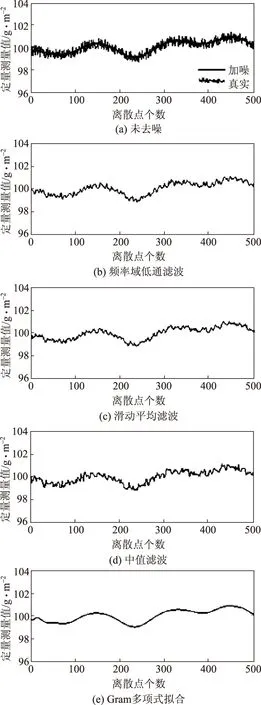
图4 含均值噪声的定量测量数据去噪

为检验该算法对纸机生产中纸张定量测量数据的去噪效果，利用模拟数据进行仿真实验。纸幅定量是连续的，为此可以用若干正弦/余弦曲线以及斜坡信号的叠加作为纸幅定量的真实值(见图3(a))。真实纸机O型扫描架从纸幅一端到另一端的扫描点个数一般为500，本实验也对连续信号进行500个点采样，并在此离散信号上分别加入方差0.16的高斯噪声和幅值0.5的均匀分布噪声。为了对比去噪效果，分别采用频率域低通滤波、滑动平均滤波、中值滤波和本研究方法进行去噪(见图3、图4)。

其中，频率域低通滤波采用的是FIR数字滤波器。FIR滤波过程就是一个信号逐级延迟的过程，将各级延迟输出加权累加，得到滤波输出。其中涉及2个参数选取，即窗口长度以及截止频率，窗口长度越长，能实现的滤波器特性就可以越复杂，计算量也越大。

滑动平均滤波为一种均值滤波，采用一个包含奇数点的滑动窗口依次处理整个离散序列，用窗口内所有点的均值作为替换中间点的数值，是一种线性滤波。滑动平均滤波器常用于时域滤波，尽管它很简单，但是可以有效抑制随机噪声并保留陡峭边沿。中值滤波与此类似，不过是将窗口中的点排序，用中值替换窗口中间点的数值，是一种非线性滤波。它对孤立的噪声点去噪效果显著。此实验中，两者窗口长度均取为5。为了防止离散序列降维而影响比较效果，端点处用2个首点值和2个末尾点值补齐。Gram多项式次数选择没有固定法则，过低不能很好地反映原信号趋势，过高则端点处容易产生振荡，本实验选为20。

由图3、图4的仿真结果可以看出，所有的滤波方法对含噪信号都有一定的滤波效果。频率域低通滤波涉及到截止频率选取，不同的截止频率差异明显(仿真图此处未给出)，而现场干扰噪声模型未知，因此该方法适应性较差，去噪效果一般。滑动平均滤波能较好跟踪噪声陡峭边沿，毛刺趋势与含噪信号比较一致，对两种随机噪声均有较好的去噪效果。由于含噪点众多，中值滤波对此类随机噪声难以有效去除，因而中值滤波对两种噪声去噪效果均最差。Gram多项式拟合去噪，对于这种均值为0的噪声均有良好的去噪效果，可以反映真实定量的主要变化趋势，仅在边界处受噪声幅值的影响，同纸张定量真实值有较大偏离。此外，Gram多项式拟合是采用一系列多项式加权叠加得到，所以光滑性很好，更接近纸张定量的真实情况，更有利于后续对稀释水阀的控制，能有效防止误动作。

不同去噪方法Matlab仿真时间见表1。由表1可知，与其他滤波算法相比，采用Gram多项式的方法计算量略大，仿真时间略长。Gram多项式是一种正交多项式系，最小二乘估计计算量最大的矩阵求逆部分求得的是对角矩阵，大大简化了计算，速度完全能够满足后续在线控制的要求。

去噪后所得离散序列(离散点个数为500)与真实值的总标准差列于表2。由表2可知，去噪后的测量值与真实值的标准差进一步验证了Gram多项式拟合滤波方法好于其他滤波方法。当噪声幅值减小时，不同去噪方法的总标准差都会减小，但Gram多项式拟合方法的标准差仍然最小，只有在含噪点很少的极

端情况下，中值滤波才会有很好的去噪效果，但实际生产中噪声不可能仅限于几个点，所以中值滤波不具有实际应用意义。

表1 不同去噪方法Matlab仿真时间 s

表2 不同去噪方法去噪后测量值与真实值的标准差

3 结 语

Matlab仿真结果表明，Gram多项式拟合去噪方法对高斯噪声和均值噪声都有良好的去噪效果，优于传统去噪方法。Gram多项式拟合去噪方法的测量数据能反映纸张定量真实的变化趋势，而且离散数据总体平滑性较好，更接近纸张定量的真实情况，同时计算速度快，能够在线反馈给控制器。离散多项式次数选取还没有固定规则，是后续研究的重点。

参 考 文 献

[1] Kristinn Kristinsson， Guy A Dumont. Cross-directional Control on Paper Machines Using Gram Polynomials[J]. Automatica, 1996 (32): 533.

[2] 蔡志东, 张固澜, 刘振亚. 测井数据自适应多项式拟合去噪[J]. 测井技术, 2013, 37(1): 59.

[3] 梁民赞, 黄子豪, 曹占启. 曲线拟合与卡尔曼滤波器的滤波精度评估[J]. 测控遥感与导航定位, 2013, 43(3): 36.

[4] 吴建华, 李迟生, 周卫星. 中值滤波与均值滤波的去噪性能比较[J]. 南昌大学学报, 1998, 20(1): 32.