残余力向量法直接识别剪切型框架结构损伤的有效性研究

陆国东 邹万杰 陆 进

(广西科技大学土木建筑工程学院，广西 柳州 545006)

0 前 言

结构健康监测的关键环节是识别结构损伤，结构损伤识别方法是当前研究的热点和难点[1]。目前土木工程结构损伤识别的方法有基于振型、频率的方法，基于模型修正的方法，基于振动测试的方法，基于遗传算法和神经网络智能识别以及残余力向量等方法。自残余力向量法被提出之后，因其概念清楚、计算明确而备受研究关注[2]。Zimmerman和Kaouk[3]首先提出了残余力法，周先雁等人[4-5]成功运用残余力向量法结合灵敏度分析识别出了混凝土框架结构的损伤程度和损伤位置。张向东等人[6]运用残余力向量法成功识别出悬臂梁的损伤位置和损伤程度。通过改进的虚拟残余力向量作为损伤识别指标可以有效的识别结构的大小损伤以及单位置、多位置损伤[7]。残余力向量法结合灵敏度分析求出结构的刚度联系矩阵，在将损伤后的刚度摄动矩阵展开为对角阵，求出新的残余力向量，通过这种方法可以很好识别桁架结构损伤[8]。残余力向量法逐渐与灵敏度、人工神经网络技术相结合[9]，改进的残余力向量法随之出现[10]，基于残余力向量法的损伤识别优越性也更加明显。由于残余力向量法计算明确，操作易于实施，所以本文针对剪切型框架结构采用了残余力向量法。用该方法直接识别，结果表明仅需损伤结构的一阶模态即可准确识别出结构的损伤位置和损伤程度。

1 残余力向量法识别框架结构损伤的理论及方法

根据多自由度结构整体刚度矩阵，K可表示为：

K=APAT

(1)

损伤后结构刚度改变矩阵可表示为：

ΔK=AΔPAT

(2)

其中，A为结构刚度联系矩阵，A=[a1a2… an]，第i个刚度参数ki的刚度联系向量为ai，损伤前后A不变。对于n自由度体系：

其中：ki为多自由度结构第i个刚度参数；Δki为多自由度结构第i个刚度参数的改变量。

展开式(2)，其中的元素为：

(3)

由灵敏度分析知：

(4)

由式(3)、(4)可得：

(5)

由式(5)可求出Aij，即可以得到刚度联系矩阵A，ai为矩阵第i列。

对于多自由度损伤结构忽略阻尼时有：

(Kd-λdjMd)φdj=0

(6)

其中，Kd=Ku-ΔK；Md=Mu-ΔM；而Ku、Mu为多自由度结构损伤前的刚度矩阵和质量矩阵；Kd、Md分别为多自由度结构损伤后的刚度矩阵和质量矩阵；ΔK为刚度矩阵的变化矩阵；ΔM为质量矩阵的变化矩阵；λdj、φdj分别为多自由度结构损伤后的第j阶特征值与第j阶特征向量，把Kd=Ku-ΔK，Md=Mu-ΔM代入式(6)得到：

(Ku-λdjMu)φdj=(ΔK-λdjΔM)φdj=Rj

(7)

其中：Rj为第j阶残余力向量，一般情况结构的损伤质量不变即ΔM=0。由式(7)可得：

ΔKφdj=Rj

(8)

展开(2)得到式(9)：

(9)

将式(9)代入式(8)得：

(10)

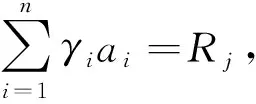
Aγ=Rj

(11)

(12)

最后与已知损伤比较验证该方法的有效性[13]。

2 算例分析

图1所示为某5层剪切型框架结构。忽略阻尼影响，根据简化原理对结构进行简化：将质量集中在楼层，故自由度数量为5，侧移刚度数量也为5，故刚度联系矩阵A为方阵而且满秩，直接由式(11)可以求出γ，最后由本文提出的方法对其损伤工况进行识别。已知各楼层质量mi=5×105kg，(i=1～5)，各个楼层侧移刚度ki=2×108Nm，(i=1～5)，结构一、三层刚度受损，分别降低了5%和10%，即k1下降为1.9×108Nm，k3下降为1.8×108Nm。

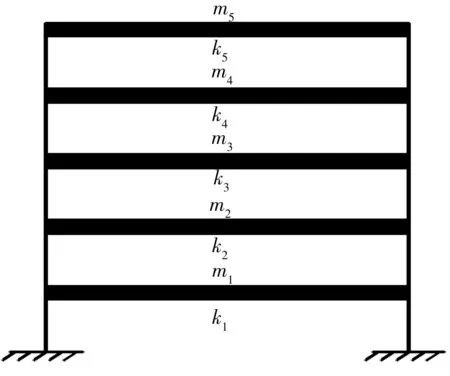
图1 5层剪切型框架结构

此5层剪切型框架结构的质量矩阵为：

其刚度矩阵为：

由式(5)得到此结构刚度联系矩阵A：

损伤框架的第一阶模态参数为(数值算例由ANSYS直接求得)：

λd1=0.311×102(rad2s2)

φd1=10-3×[0.165 1 0.309 1 0.442 4 0.528 0 0.572 5]T

由一阶模态参数计算得到残余力向量：

R1=104×[0.165 1 -0.133 3 0.133 3 0 0]T

再根据式(11)得出γ：

γ=104×[0.165 1 0 -0.133 3 0 0]T

最后由式(12)求出：

Δk=107×[1 0 2 0 0]T(N/m)，Δk1=107(N/m) ，Δk3=2×107(N/m)

损伤发生在一层和三层，其侧移刚度分别降低为5%和10%，与已知损伤工况一致，该方法的有效性得以验证。

3 结 语

通过以上分析，重点介绍基本理论和残余力向量对结构损伤的直接识别方法。用残余力向量法识别结构损伤，只需损伤后结构的一阶模态即可识别结构的损伤程度和损伤位置，损伤后结构的一阶模态在数值算例中由ANSYS软件计算更加简单方便，因此该方法易于实施。以某已知损伤工况的框架结构为例，应用文中方法成功地识别出结构的损伤状况，验证了该方法的有效性。

[1] 秦权. 桥梁结构的健康监测[J]. 中国公路学报, 2000,13(2)：37-42.

[2] 王博，何伟，李静斌.残余力向量法在结构损伤识别中的应用研究进展[J].实验力学,2010,25(1)：47-51.

[3] Zimmerman D C, Kaouk M. Structural Damage Detection in Beam Structures Using a Subspace Rotation Algorithm [J]. AIAA Journal, 1992, 34(12): 2341-2350.

[4] 周先雁，沈浦生. 用振动参数识别技术对混凝土框架结构进行破损评估[J]. 土木工程学报，1998，31(2)：39-45.

[5] 周先雁.用动力法对混凝土平面框架结构进行损伤诊断[J]. 湖南城市学院学报，2003，24(3)：1-3.

[6] 张向东，王志华，马宏伟. 基于残余力向量法的悬臂梁损伤识别研究[J]. 太原理工大学学报，2003，34(5)：529-531.

[7] 韦灼彬，吴森.基于残余力向量法的结构损伤位置识别[J]. 中外公路，2011，31(1)：177-180.

[8] 蔡小双，纪国宜.基于残余力向量法的桁架结构损伤识别[J]. 工业建筑，2013，43(12)：211-213.

[9] 周宁娜，史兴岭，南洪.论梁结构损伤的诊断方法[J]. 水利与建筑工程学报，2010，8(1)：140-143.

[10] 何伟，陈淮，王博，等.运用改进残余力向量法的结构损伤识别研究[J]. 振动、测试与诊断，2009，29(4)：379-382.

[11] 姜绍飞.结构健康监测导论[M]. 北京: 科学出版社, 2013.

[12] Doebling S W. Minimum-Rank Optimal Update of Elemental Stifness Parameters for Structural Damage Identification[J]. AIAA Journal,1996,34(12):2615-2621.

[13] 邹万杰，瞿伟廉. 基于残余力向量法的桁架结构损伤直接识别法[J]. 广西工学院学报，2009,20(1): 31-34.