基于TIGGE资料的北半球地面气温预报的统计降尺度研究
2014-08-13陈晓龙智协飞
陈晓龙,智协飞
(1.气象灾害教育部重点实验室(南京信息工程大学),江苏南京210044;2.南京信息工程大学大气科学学院,江苏南京210044)
0 引言
随着社会经济的发展和人民生活水平的提高,政府和公众对于气象服务的需求日益增加,不仅要求气象部门提供常规天气预报服务,还希望获取更高精度的天气服务信息。因此,精细化预报是我国现在和未来天气预报发展的一个重要战略目标,实现空间尺度的精细化更是精细化预报的一项重要内容。目前有两种方法可以提供精细化预报,一是发展更高分辨率的数值模式,另外就是采用降尺度方法。由于提高数值模式的空间分辨率不仅计算量很大,而且技术也较复杂,以目前的技术条件还做不到任意提高区域模式的分辨率,与之相比降尺度方法具有可操作性较强、计算量较小、对于实际业务更为实用等优点,因此开展降尺度研究显得十分重要。
常用的降尺度方法一般可分为两种:一种是统计降尺度法(Wilby et al.,1997;范丽军等,2005),另一种是动力降尺度法(Rebora and Provenzale,2005)。统计降尺度法是建立大尺度预报因子与小尺度预报量之间的统计函数关系。该方法的优点在于其能将数值模式输出的物理意义较好、较准确的数值预报产品应用于统计模式,从而减少数值模式的系统误差,并且不必考虑边界条件对预测结果的影响。与动力降尺度方法相比,统计降尺度法还具有计算量相对较小以及能够模拟很多非气象要素场等优点,在实际业务与研究中更具可操作性。近年来统计降尺度方法主要集中在降水与气温预报方面(Kanamaru and Kanamitsu,2007;Brankovi et al.,2008;Yoshimura and Kanamitsu,2008;Cañón et al.,2011)。一般可分为以下三类:转换函数法,环境分型技术,天气发生器。其中转化函数法被广泛使用,后两种方法常用于时间尺度较长的气候场上。Sailor and Li(1999)用多元线性回归方法模拟了美国站点的气温,明显地提高了预报准确率。范丽军等(2007)采用逐步回归分析与主分量分析相结合的多元回归模型对华北地区未来月平均温度变化情景进行预估,发现统计降尺度得到的温度预报与实测值有很好的一致性。近些年来国内对于统计降尺度方法的研究主要集中在对时间尺度较长的未来区域气候情景变化的预估方面,而将统计降尺度方法应用于中短期预报的则不多见。最近,王亚男和智协飞(2012)利用全球交互式大集合(THORPEX Interactive Grand Global Ensemble,TIGGE)预报资料和TRMM/3B42RT合成降雨量资料对降水的1~7 d预报进行了统计降尺度试验,发现单个中心降水预报经过统计降尺度后,预报误差明显减小,与“观测场”的距平相关系数也明显提高。
Lorenz(1969)最早提出了集合数值预报的思想。20世纪90年代开始,集合预报技术在许多国家气象部门相继投入业务使用。近年来,世界气象组织(World Meteorological Organization,WMO)发起的THORPEX科学计划中的TIGGE计划提出了建立全球交互式大集合预报,以改进预报时效为1~14 d天气预报(智协飞和陈雯,2010)。WMO在中国气象局、欧洲中期天气预报中心和美国国家大气研究中心设立了3个TIGGE资料中心,每天接收数十个国家的集合预报资料。比较各中心的预报效果和如何更好地利用各中心的模式预报资料来提高业务预报的准确率也已成为近年来国内外的研究热点。Krishnamurti et al.(1999)最早提出了一种多模式集合预报方法即超级集合预报。研究发现,超级集合预报可有效减小预报或者预估误差,预报效果优于单个模式和多模式集合平均(Vijaya Kumar et al.,2007;林春泽等,2009;Krishnamurti et al.,2009;智协飞等,2009,2013;Zhi et al.,2009,2011)。另外,Zhi et al.(2012)还指出,消除偏差集合平均方法也能显著提高地面气温和降水的1~7 d预报技巧,其预报误差比最好的单个中心预报误差都小。
本文主要对欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)、日本气象厅(Japan Meteorological Agency,JMA)、美国国家环境预报中心(National Centers for Environmental Prediction,NCEP)以及英国气象局(United Kingdom Met Office,UKMO)4个中心的2 m气温预报资料,采用统计降尺度法,并结合多模式超级集合预报思想,生成较高分辨率的北半球地面气温预报,从而为气象业务部门开展精细化预报提供有益的指导。
1 资料和方法
1.1 资料
本文所用资料包括TIGGE中的ECMWF、JMA、NCEP和UKMO集合数值预报资料以及NCEP/NCAR再分析资料。后者被用作“实况场”来评估预报效果。
1)TIGGE资料:选取4个中心的全球集合预报模式2007年6月1日—8月31日逐日12:00(世界时,下同)起报的地面2 m气温的各成员预报资料,为了便于分析预报效果,分别将4个中心各自成员的模式预报资料进行集合算术平均,预报区域为北半球主要地区(0°~355°E,10 ~85°N),分辨率为2.5°×2.5°,预报时效为1 ~7 d,间隔为1 d。
2)NCEP/NCAR再分析资料:选取2007年6月2日—9月7日逐日12:00地面2 m气温资料,网格分辨率为2.5°×2.5°与1°×1°(其中1°×1°分辨率的FNL再分析资料用来检验降尺度后的预报效果)。
1.2 统计降尺度方案
采取三个步骤对地面气温进行统计降尺度预报。
1)采用双线性插值方法将低分辨率的模式预报结果插值到细网格上,即在指定的预报区域内,将各中心模式预报值统一插值到1°×1°经纬网格上。
2)降尺度之后的误差订正。在每一个格点上,建立起预报值与“实况值”之间的回归关系,订正模式插值引起的误差。考虑到气温的连续性并服从正态分布,经试验采用一元线性回归方法进行降尺度之后的误差订正。

其中:Xi是插值后的模式预报序列;Yi是相对应的细网格观测值序列;在训练期中确定回归系数a、b。在预报期中,根据插值后的数据Xi,利用回归方程(1)可以算得预报值Yi。
3)对于降尺度订正后的各中心结果再进行多模式集成,集成方案主要采用以下两种。
第一种:消除偏差集合平均(bias-removed ensemble mean,BREM)。消除偏差集合平均预报值BREM由下式获得:
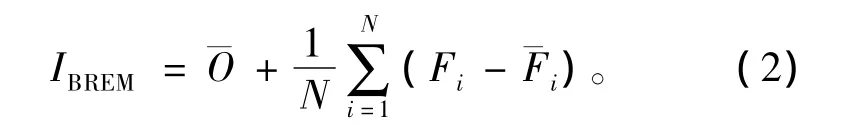
对每一个格点,Fi为第i个模式的预报值,¯Fi为第i个模式预报值平均,¯O为观测值平均,N为参与集成的模式个数。
第二种:超级集合预报方法。超级集合方法赋予各个模式不同的权重系数,在训练期中根据各个模式的预报性能来确定权重系数。通常预报误差越大的模式所赋的权重越小,反之预报误差越小,所赋权重越大。在训练期可使用线性回归方法(林春泽等,2009;智协飞等,2009;Zhi et al.,2011)或神经网络方法等(白永清,2010)求出参与多模式集成的各个模式的权重系数。超级集合预报值(superensemble,SUP)由下式获得:
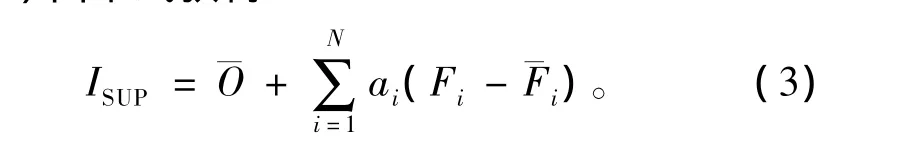
其中:¯O为训练期的观测值平均;Fi为第i个模式的预报值;¯Fi为第i个模式在训练期的预报值的平均值;ai为回归系数(权重);N为参与超级集合的模式总数。参与集成的模式权重总和为1,权重系数可取训练期各模式预报的平均误差的倒数,也就是说模式预报误差越小,或者预报评分越高,在多模式集成中所占的权重系数就越大。本文用到的权重为模式训练期预报的均方根误差的倒数。
在上述两种降尺度订正之后的集合方法中均采用交叉检验的方案,即从资料序列的第一个样本开始,每次轮流留出一个样本,用余下的样本建立预报方程,并对留出的样本作预报检验。这样依次进行,直到全部样本都作为独立的预报检验完毕。这种方法的优点就是能充分利用所有的资料。
1.3 误差检验标准
本文主要采用均方根误差(root-mean-square error,RMSE)来评价气温预报的技巧,均方根误差由(4)式给出:
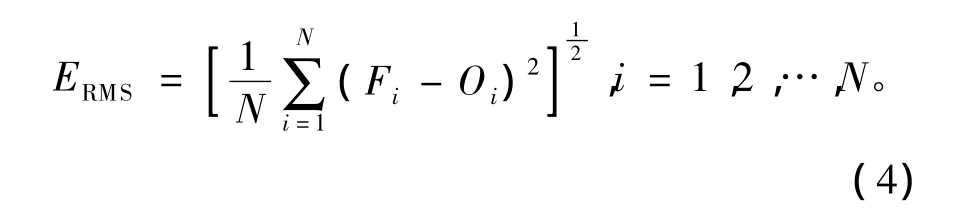
其中:Fi为模式输出的预报值;Oi为观测的实况值;N为样本总数。
2 北半球地面气温单中心预报的统计降尺度
以均方根误差作为衡量温度预报效果的指标,计算2007年6月1日—8月31日4个中心地面气温预报在北半球地区(0°~355°E,10 ~85°N)的区域平均均方根误差。如图1所示,对于北半球大部地区4个中心预报的均方根误差随预报时效增加而增大。降尺度前4个单中心预报中综合表现最好的是ECMWF,其1 d预报误差为2.22℃,7 d预报的误差为2.65℃;综合表现最差的是UKMO,其1 d预报的误差为2.62℃,7 d预报的误差达到了3.11℃。
分别对各中心进行统计降尺度试验,4个中心的地面气温预报误差都有了较为明显的减小。其中,原来表现最好的单中心ECMWF的1 d预报误差由原来的2.22℃降低到1.30℃,7 d预报的误差从2.65℃降低到1.94℃。原来表现较差的单中心UKMO的1 d预报误差也由2.62℃减小到1.43℃,7 d预报的误差更是从3.11℃降低至2.07℃,预报效果的改善更为明显。对于4个单中心7个预报时效的预报在降尺度后误差都明显减小,各预报时效的预报误差降幅维持在0.6℃左右,最大的改进幅度甚至达到了1℃以上,预报效果得到明显改进。
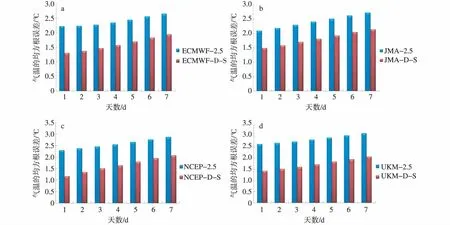
图12007年6月1日—8月31日ECMWF(a)、JMA(b)、NCEP(c)和UKMO(d)4个中心统计降尺度前后北半球地面气温预报的区域平均均方根误差(单位:℃;-2.5表示降尺度前预报的均方根误差,-D-S表示降尺度后的均方根误差)Fig.1 The areal average RMS errors of the surface temperature forecast from(a)ECMWF,(b)JMA,(c)NCEP and(d)UKMO in the Northern Hemisphere during the period from 1 June to 31 August 2007(units:℃;-2.5 represents the RMS error of the forecast before the statistical downscaling,while -D -S represents that after the statistical downscaling)
图2给出了2007年6—8月3个月内单中心预报降尺度前后地面气温预报均方根误差的地理分布(以ECMWF的1 d预报和7 d预报为例)。从图2中可以看出,相对而言,ECMWF在亚洲大陆的预报误差较大,特别是在青藏高原地区,1 d预报的误差在个别地区甚至超过5℃。这可解释为复杂的高原地形导致数值预报准确率低。当然,高原地区实测资料稀少也可能导致预报和实况值之间较大的偏差。北美地区预报误差相对较小。其他3个中心也有类似的结果(图略)。在做了降尺度订正之后,北半球绝大部分地区的误差都有明显的下降,对于1 d预报而言,误差基本稳定在2.5℃之内,原来误差较大的青藏高原地区改善更显著,误差降到了3℃以内。7 d预报的改善效果类似。
3 多模式集成的北半球地面气温预报的统计降尺度
通过对4个单个中心的降尺度预报试验,地面气温1~7 d的预报的均方根误差均明显降低。各个中心的预报技巧不一,改进的幅度也略有差异。为了进一步改进降尺度预报效果,对各个中心降尺度预报进行多模式集成。多模式集成方案主要选取以下两种:消除偏差集合平均(BREM)和超级集合预报(SUP)。
图3给出了最好的单中心ECMWF 1~7 d降尺度预报和降尺度后的多模式集成预报北半球区域平均的逐日均方根误差。图3显示,对于1~7 d 7个预报时效,降尺度订正之后的超级集合预报方法(D-SUP)和降尺度订正之后的消除偏差集合平均方法(D-BREM)都能有效地减小模式的预报误差。引入上述两种集成方案的统计降尺度预报效果要明显优于ECMWF的预报效果。在预报期内,两种方法的平均均方根误差相差不大,D-SUP的误差略小于D-BREM。
在预报期内,对于1 d预报,D-SUP和D-BREM的均方根误差都维持在1.2℃左右,比ECMWF的预报误差减少了近1℃,较之UKMO误差更是降低了1.4℃左右,预报准确率得到明显提高。随着预报时效的延长,两种方案的均方根误差也在增加。对于7 d预报,D-SUP和D-BREM 的均方根误差在1.6~2.4℃之间波动,比UKMO 1 d的预报误差还要小。可见,这两种多模式集成方案都能明显改进中短期地面气温的预报技巧。

图2 2007年6—8月降尺度前后ECMWF地面气温预报的均方根误差的分布(单位:℃) a.原始ECMWF 1 d预报;b.降尺度订正后的ECMWF 1 d预报;c.原始ECMWF 7 d预报;d.降尺度订正后的ECMWF 7 d预报Fig.2 The geographic distribution of the RMS errors of the ECMWF surface temperature forecast before and after the statistical downscaling during the period from 1 June to 31 August 2007(units:℃) a.the 1 d forecast before the statistical downscaling;b.the 1 d forecast after the statistical downscaling;c.the 7 d forecast before the statistical downscaling;d.the 7 d forecast after the statistical downscaling
图4是降尺度之后两种多模式集成方案对比最好的单中心ECMWF和综合表现最好的单模式降尺度ECMWF及其统计降尺度预报的均方根误差改进百分率。对比单中心ECMWF模式预报,降尺度后再进行多模式集成,7个预报时效的预报误差均明显减小,改进百分率在22% ~45%之间,1 d预报的改进百分率达到了45%左右,误差改进百分率随着预报时效的延长而减小,D-SUP较D-BREM 预报的改进幅度略高。对比ECMWF降尺度方案,DSUP和D-BREM 1~7 d预报均方根误差的改进相对较小,在2% ~13%之间,这主要是因为单中心降尺度预报本身已大大地减小了原始模式的误差。同时也可看出,D-SUP方案预报效果略优于D-BREM方案。

图32007年 8 月1—31日1 d(a)、2 d(b)、3 d(c)、4 d(d)、5 d(e)、6 d(f)和7 d(g)北半球地面气温预报的区域平均均方根误差(单位:℃)Fig.3 The areal average RMS errors of the surface temperature forecast in the Northern Hemisphere for(a)1 d,(b)2 d,(c)3 d,(d)4 d,(e)5 d,(f)6 d and(g)7 d during the period from 1 to 31 August 2007(units:℃)
4 不同插值方法对降尺度预报效果的影响
在大气科学研究中常用的插值方法有很多。姜晓剑等(2010)曾对几种不同的逐日气象要素空间插值方法进行了比较。对地面气温而言,常见的有双线性插值(Bilinear,Bi)、拉格朗日插值(Lagrange,LAR)、样条函数插值(Spline,SPL)、克里金插值(Kriging,KRI)和距离反比权重插值(Inverse Distance Weighted,IDW)等(李伟等,2007;张强等,2009;钱永兰等,2010)。在上述统计降尺度研究中,本文采用的插值方法均为双线性插值。那么,对于本研究双线性插值是否为最优的插值方法呢?为此,在统计降尺度方案中首先采用4种不同的插值方法(BI、IDW、SPL、LAR)分别对4个中心预报进行插值。降尺度后再进行两种方案的多模式集成(SUP与BREM),然后比较各种方案的预报技巧。
如图5所示,就本文研究的区域和使用的降尺度集成方案而言,四种插值方法对于降尺度集成预报效果的影响并不是很大。效果最好的是双线性插值方法,除了个别预报时效外,绝大部分预报时效的预报均方根误差均小于利用其他3种插值方法的降尺度集成方案的结果。综合效果最差的是拉格朗日插值(LAR),预报时效为1~2 d、6~7 d的预报误差都是最大,特别是7 d预报时效的预报误差明显大于其他3种插值方法的预报误差,达到2℃以上,而其他三种插值方法的预报误差均不超过2℃。
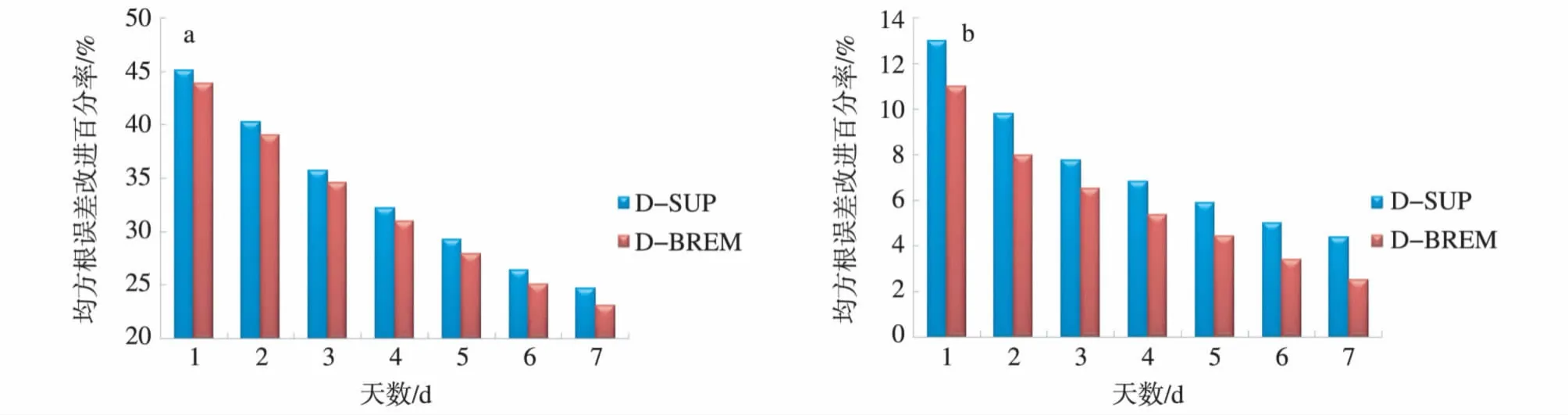
图4 降尺度后两种多模式集成预报方案的均方根误差改进百分率 a.对比综合表现最好的单中心ECMWF模式预报;b.对比综合表现最好的单中心ECMWF统计降尺度预报Fig.4 The improvement percentage of the RMS errors of the downscaling with BREM and SUP forecast schemes and multimodel ensemble forecast over(a)the best single model ECMWF forecast and(b)the best single model ECMWF statistical downscaling forecast
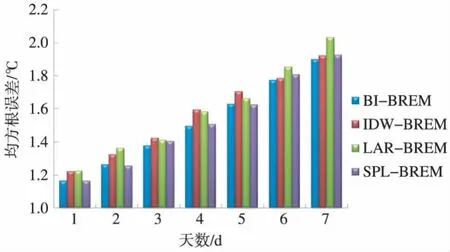
图5 利用4种不同插值方法的降尺度和多模式集成预报的均方根误差对比Fig.5 Comparison of the RMS errors of the statistical downscaling and multimodel ensemble forecasts by using 4 different interpolation schemes
5 结论与讨论
本文对ECMWF、JMA、NCEP和UKMO 4个中心2007年夏季北半球地面2 m气温1~7d预报的集合平均预报资料,利用双线性插值方法、线性回归分析和两种多模式集成预报方案(SUP和BREM)进行统计降尺度预报研究,得到如下几点结论。
1)2007年夏季,4个中心的北半球地面气温预报经过统计降尺度处理后,其预报误差都明显减小。对比降尺度前的预报,统计降尺度后各预报时效的预报误差降幅维持在0.6℃左右,最大的改进幅度甚至达到了1℃以上。
2)降尺度后再采用多模式超级集合和去除偏差集合平均两种集成预报方案,预报技巧得到进一步提高,两种集成方案对预报的改进效果相当。对比综合表现最好的单中心ECMWF预报,7个时效的统计降尺度及多模式集成预报的误差明显减小,预报误差减小了20%以上,最高可达45%。对比综合表现最好的单中心ECMWF降尺度方案,均方根误差减小2% ~13%。其中,基于超级集合预报的降尺度方案(D-SUP)预报误差小于基于消除偏差集合平均的降尺度方案(D-BREM)。
3)综合比较双线性插值、拉格朗日插值、样条函数插值和距离反比权重插值4种插值方法,效果最好的是双线性插值方法,除了个别预报时效外,绝大部分预报时效的预报均方根误差均小于利用其他三种插值方法的降尺度集成方案的结果。综合效果最差的是拉格朗日插值方法,特别是7 d预报时效的预报误差明显大于其他3种插值方法的预报误差,达到2℃以上。
由于本文所使用的各个中心的模式预报资料均是在夏季3个月中,对于冬季或其他季节的预报效果检验还有待进一步研究。而由于检验资料精度的限制,本文所用的降尺度预报方案均是把原始资料降到了1°×1°的分辨率,当然这种方法也同样适合做更高分辨率的预报,这取决于能否获得更高分辨率的实测资料。随着加密自动站资料的质量控制技术的发展以及各种融合资料的完善,未来将可利用统计降尺度方法及多模式集成方法得到更好的精细化预报。
白永清.2010.基于TIGGE资料多模式地面气温和降水的集成预报[D].南京:南京信息工程大学.
范丽军,符淙斌,陈德亮.2005.统计降尺度法对未来区域气候情景预测的研究进展[J].地球科学进展,20(3):320-329.
范丽军,符淙斌,陈德亮.2007.统计降尺度法对华北地区未来区域气温变化情景的预估[J].大气科学,31(5):887-897.
姜晓剑,刘小军,黄芬,等.2010.逐日气象要素空间插值方法的比较[J].应用生态学报,21(3):624-630.
李伟,李庆祥,江志红.2007.用Kriging方法对中国历史气温资料插值可行性讨论[J].南京气象学院学报,30(2):246-252.
林春泽,智协飞,韩艳,等.2009.基于TIGGE资料的地面气温多模式超级集合预报[J].应用气象学报,20(6):706-712.
钱永兰,吕厚荃,张艳红.2010.基于ANUSPLIN软件的逐日气象要素插值方法应用与评估[J].气象与环境学报,26(2):9-15.
王亚男,智协飞.2012.多模式降水集合预报的统计降尺度研究[J].暴雨灾害,31(1):1-6.
张强,阮新,熊安元.2009.近57年我国气温格点资料集的建立和质量评估[J].应用气象学报,20(4):385-393.
智协飞,陈雯.2010.THORPEX国际科学研究新进展[J].大气科学学报,33(4):504-511.
智协飞,林春泽,白永清,等.2009.北半球中纬度地区地面气温的超级集合预报[J].气象科学,32(5):569-574.
智协飞,季晓东,张璟,等.2013.基于TIGGE资料的地面气温和降水的多模式集成预报[J].大气科学学报,36(3):257-266.
Brankovic C,Matjacic B,Sahdan I.2008.Downscaling of ECMWF ensemble forecasts for cases of severe weather:Ensemble statistics and cluster analysis[J].Mon Wea Rev,136:3323-3342.
Caňón J,Domínguez F,Valdes J B.2011.Downscaling climate variability associated with quasi-periodic climate signals:A new statistical approach using MSSA[J].J Hydrol,398:65-75.
Kanamaru H,Kanamitsu M.2007.Fifty-seven-year California reanalysis downscaling at 10 km(CaRD10).PartⅡ:Comparison with North American regional reanalysis[J].J Climate,20:5572-5592.
Krishnamurti T N,Kishtawal C M,LaRow T,et al.1999.Improved weather and seasonal climate forecasts from multimodel superensemble[J].Science,285:1548-1550.
Krishnamurti T N,Mishra A K,Chakraborty A.2009.Improving global model precipitation Forecasts over India using downscaling and the FSU superensemble.Part Ⅰ:1—5-Day forecasts[J].Mon Wea Rev,137:2713-2735.
Lorenz E N.1969.A study of the predictability of 28-variable atmosphere model[J].Tellus,21:739-759.
Rebora N,Provenzale L.2005.Rain FARM:Rainfall downscaling by a filtered autoregressive model[J].J Hydrometeorol,7:724-738.
Sailor D J,Li Xiangshang.1999.A semiempirical downscaling approach for predicting regional temperature impacts associated with climatic change[J].J Climate,12:103-114.
Vijaya Kumar T S V,Sanjay J,Basu B K,et al.2007.Experimental superensemble forecasts of tropical cyclones over the Bay of Bengal[J].Nat Hazards,41:471-485.
Wilby R L,Wigley T M L,Conway D,et al.1997.Downscaling general circulation model output:A review of methods and limitations[J].Progress in Physical Geography,21:530-548.
Yoshimura K,Kanamitsu M.2008.Dynamical global downscaling of global reanalysis[J].Mon Wea Rev,136:2983-2998.
Zhi Xiefei,Bai Yongqing,Lin Chunze,et al.2009.Multi-model superensemble forecasts of the surface temperature in the Northern Hemisphere[C]//Third THORPEX international science symposium.California:14-18.
Zhi Xiefei,Zhang Ling,Bai Yongqing.2011.Application of the multimodel ensemble forecast in the QPF[C]//2011 international conference on information science and technology.Nanjing:657-660.doi:10.1109/ICIST.2011.5765333.
Zhi Xiefei,Qi Haixia,Bai Yongqing,et al.2012.A comparison of three kinds of multimodel ensemble forecast techniques based on the TIGGE data[J].Acta Meteor Sinica,26(1):41-51.doi:10.1007/s13351-012-0104-5.
