Importance Analysis of a Multi-state System Based on Direct Partial Logic Derivatives and Multi-valued Decision Diagrams

GU Ying-kui (古莹奎), LI Jing (李 晶)

School of Mechanical and Electronical Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China

Importance Analysis of a Multi-state System Based on Direct Partial Logic Derivatives and Multi-valued Decision Diagrams

GU Ying-kui (古莹奎)*, LI Jing (李 晶)

SchoolofMechanicalandElectronicalEngineering,JiangxiUniversityofScienceandTechnology,Ganzhou341000,China

Importance analysis quantifies the critical degree of individual component. Compared with the traditional binary state system, importance analysis of the multi-state system is more aligned with the practice. Because the multi-valued decision diagram (MDD) can reflect the relationship between the components and the system state bilaterally, it was introduced into the reliability calculation of the multi-state system (MSS). The building method, simplified criteria, and path search and probability algorithm of MSS structure function MDD were given, and the reliability of the system was calculated. The computing methods of importance based on MDD and direct partial logic derivatives (DPLD) were presented. The diesel engine fuel supply system was taken as an example to illustrate the proposed method. The results show that not only the probability of the system in each state can be easily obtained, but also the influence degree of each component and its state on the system reliability can be obtained, which is conducive to the condition monitoring and structure optimization of the system.

multi-statesystem(MSS);importanceanalysis;reliability;multi-valueddecisiondiagram(MDD);directpartiallogicderivative(DPLD);dieselenginefuelsupplysystem

Introduction

Importance measures quantify the criticality of various components within a system, and help prioritize the reliability improvement activities[1-2]. Specifically, these measures identify the components or locations that contribute the most to the overall system reliability (or weakness), and thus help identify good candidates to upgrade so the entire system reliability can be best improved[3]. Various research efforts have been devoted to generalizing or extending the existing frequently-used importance measures for binary-state systems to accommodate the multi-state behavior[2]. A detailed analysis of the current situation in importance analysis was presented in Refs. [4-7]. In this paper, the multi-valued decision diagrams (MDDs) and logical differential calculus were used to analyze the importance measures of the diesel engine fuel supply system. Compared with other existing importance measures analysis approaches, it will offer even lower computational complexity.

1 MDD

MDD is an extension of the binary decision diagram (BDD). MDD is a directed acyclic graph (DAG) of multi-state system (MSS) representation method. It has three components, circle, box, and unidirectional arrow. In MDD, the sum of all paths probability from the root node to the sink node is the probability of the system in a certain state. Each MDD is a DAG with two and only two sink nodes, and is labeled by a distinct logic value 0 or 1 representing the system not being/being in a particular state, respectively. Each non-sink node in MDD representing a multi-state component is associated with a multi-valued variable and has multiple outgoing edges. Each edge is corresponding to a specific state of the component. A detailed introduction of MDD was presented in Refs. [1-3]. To calculate the probability of the system in a certain state, we can start to directly find all paths from the root node to the sink node in MDD, and calculate the path probability. Therefore, to calculate the system state probability in MDD, we can start to traversal from top to down in the structure diagram, find out all paths to the desired state, and finally calculate the probability by some logical operators. The paths from the top non-sink node to the zero-sink node are analyzed for MSS failure[5].

2 The Logical Differential Calculus

(1)

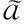
In reliability analysis of the MSS, a DPLD with componentxiis defined as,

(2)

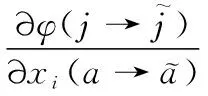
3 Importance of an MSS Based on DPLD

DPLD allow to present changes in MSS performance level depending on system component state change. The calculation algorithms for importance measure will be provided based on the logical differential calculus. Algorithms used to calculate these measures are implemented based on the logical differential calculus and allow quantifying probabilities of MSS failure depending on changes of theith system component states[5].

(1) Brinbaum importance (BI)

BI is a probabilistic measure that can be interpreted as the rate at which the MSS fails as theith system component state decreases[5],

I(BI)si= |Pr(φ(X)=1|xi=si)-Pr(φ(X)=

1|xi=si-1)|.

(3)

The physical meanings express the influence size of the system performance deterioration by the deterioration of the system’s component quality.

BI of a componentcan be defined as

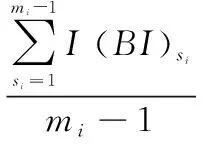
(4)

I(BI)si= |Pr(φ(X)=j|xi=si)-Pr(φ(X)=

j|xi=si-1)|.

(5)

The conditional probability of the expression on the right can be directly obtained from the MDD.

(2) Structure importance (SI)

SI is one of the simplest measures of component importance, and this measure focuses on the topologicalstructure of system. SI of theith component in statesishows the probability of reducing the system performance by the only reason of the component state changed fromsitosi-1[5].

(6)

whereρi, siis the number of system states when the component state changes fromsitosi-1. It will result in the system failure, and this number can be calculated as numbers of non-zero values of DPLD.

Every component hasmistates, and the SI of system component can be defined as

(7)

(3) Fussell-vesely importance (FVI)

FVI quantifies the maximum decrement in system reliability caused by theith system component state deterioration. FVI for an MSS represents a probabilistic measure of theith component state deterioration influence on failure of the system[5],

(8)

Consider generalizations of FVI expressed by Eq. (8) as the average value of this measure,

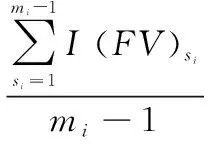
(9)

It quantifies the contribution of each component state change to the probability of a system failure.

(4) Reliability achievement worth (RAW)

RAW represents reliability increasing equivalent, and it describes the influence of the system state depending on changes in the reliability of the system component. RAW for MSS is defined as the ratio of MSS unreliability if theith component state decreases[5],

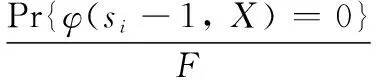
(10)

The generalization of RAW expressed by Eq. (10) for all states of theith MSS component is calculated as,

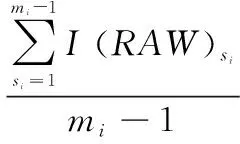
(11)

(5) Reliability reduction worth (RRW)

RRW represents reliability reducing equivalent, and can be interpreted as the opposite importance measure to RRW. The RRW of theith system component in an individualsistate can be defined as[5],

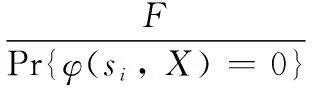
(12)

The RRW of theith component can be defined for the MSS as

(13)

4 Case Study

Take the diesel engine fuel supply system as an example to illustrate the proposed method. The system has three components,i.e.n=3. Componentx1has four states,i.e. 0, 1, 2, 3. Componentx2andx3has three states respectively,i.e. 0, 1, 2. The component state vector ism=(m1,m2,m3)=(4, 3, 3).

Table 1 Structure function of the oil supply sub-system

Based on the basic theory and operational rule of MDD, the MDD structure of the fuel supply system can be obtained. The system has four states, and their corresponding sub-graphs are shown in Fig.1.

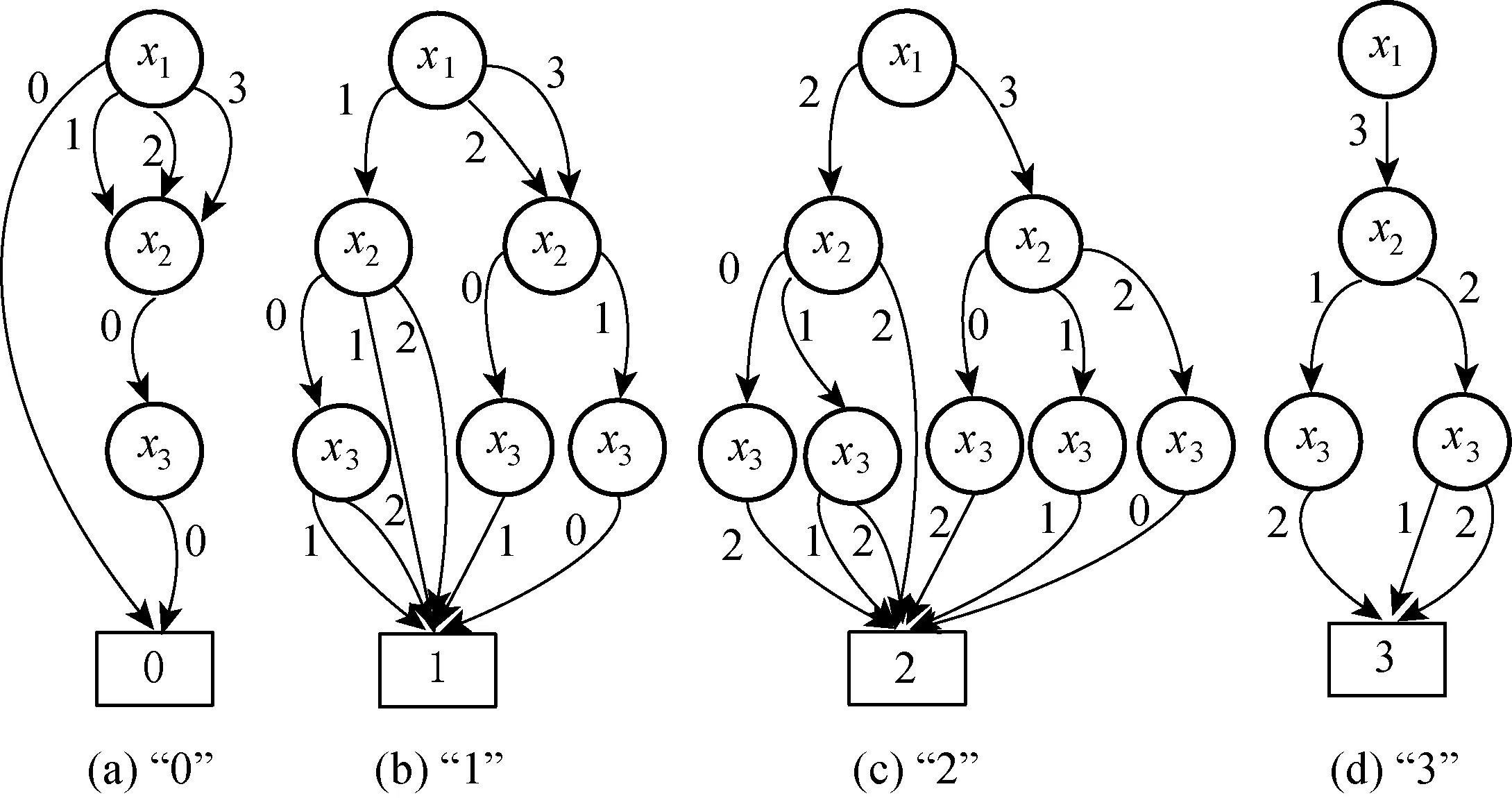
Fig.1 Sub-graphs of each system state

In Fig.1, the three components have twelve combination states when the system is in state 0, twelve combination states when the system is state 1, nine combination states when the system is in state 2, and three combination states when the system is in state 3. We can obtain the DPLD with respect to the componentsx1andx2respectively, as shown in Tables 2 and 3.

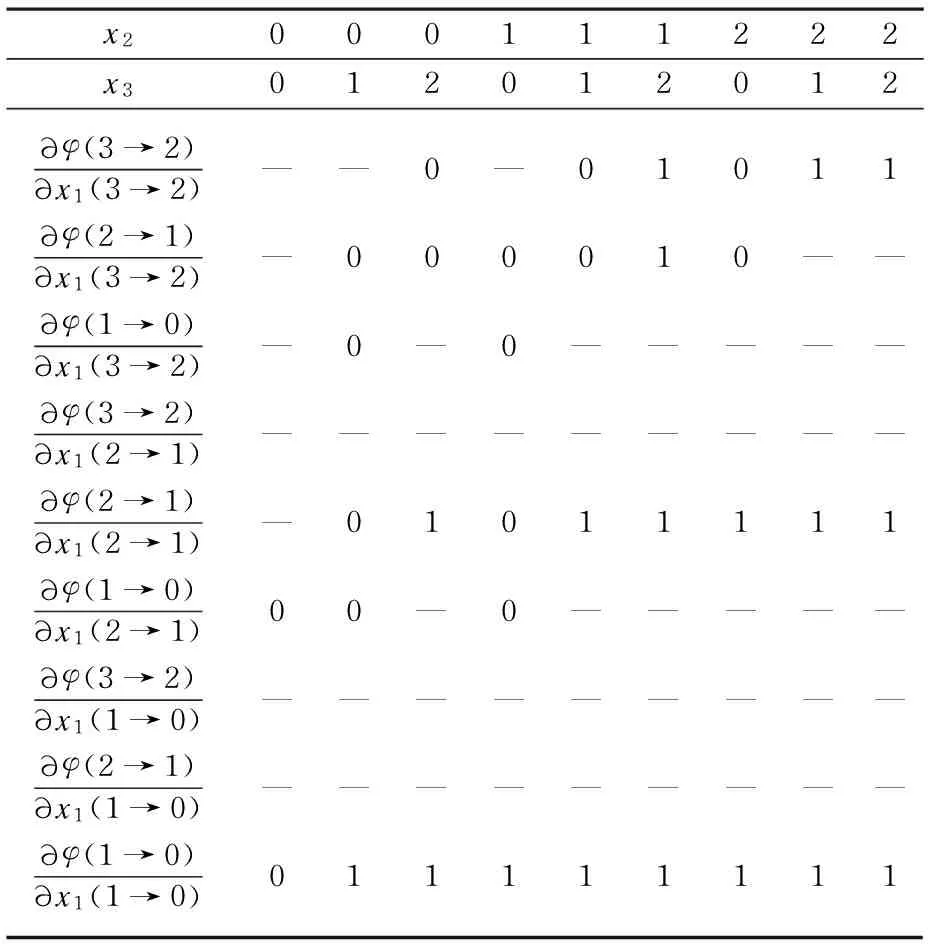
Table 2 DPLD of the MSS structure function with respect to x1

Table 3 DPLD of the MSS structure function with respect to x2

Tables 2 and 3 indicate the deterioration case of the component system, that is to say, the state of component fromstos-1.

Given the state probability of every component, the conditional probability values of each state of system components can be calculated as shown in Table 4.

Table 4 Results for conditional probability

Also, the importance value of each component in each state can be calculated based on the calculation formulas and is shown in Figs.2-4 respectively.

As can be seen from Figs.2-4, the importance value ofx1is the biggest. From the view of the systematical topologic structure,x1is in the most important position. In BI analysis,x1has the maximal influence on system failure. The state 1 ofx1is more important than the other state, because its next deterioration state is failure state. Althoughx2andx3are in the same position, the average importance ofx3is higher than that ofx2because the reliability ofx3is higher than that ofx2. Therefore, the system fault probability is higher whenx3is degeneration or failure. FVI quantifies the decrement in system reliability caused by the component state deterioration. The FVI value ofx3is lower than that ofx2. RAW and RRW are a set of opposite concepts. Diagram of RRW importance for componentsx1,x2, andx3is shown in Fig.5.

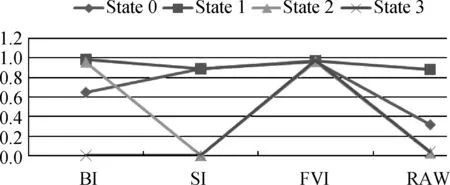
Fig.2 Diagram of importance for component x1

Fig.3 Diagram of importance for component x2

Fig.4 Diagram of importance for component x3

Fig.5 Diagram of RRW importance for components x1, x2, and x3

The values of RAW and RRW ofx1are maximal, which indicate that the unreliability of the MSS is more dependent onx1state than the other component states.

5 Conclusions

This paper presented an analytical method based on MDD and DPLD to analyze the importance of MSS. The proposed method has the following advantages.

(1) It can provide exact reliability analysis results, which will provide more accurate information for system design, modification, and optimization.

(2) It is less time-consuming to establish the analysis model, which is more visual and easy to calculate the state probability. Once the system MDD model generates, it will be reusable for importance analysis with different parameters.

(3) The MDD model can be found directly from MSS structure without enumerating minimal cut vectors or minimal path vectors.

[1] Akhilesh S, Xing L D, Coit D W. Multi-state Component Importance Analysis Using Multi-state Multi-valued Decision Diagrams [C]. Proceeding in the 8th International Conference on, Reliability, Maintainability and Safety, Chengdu, 2009: 99-103.

[2] Akhilesh S, Xing L D, Coit D W. An Efficient Multistate Multi-valued Decision Diagram-Based Approach for Multistate System Sensitivity Analysis [J].IEEETransactionsonReliability, 2010, 59(3): 581-592.

[3] Zaitseva E, Levashenko V, Kostolny J. Multi-state System Importance Analysis Based on Direct Partial Logic Derivative [C]. Proceeding in the International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Chengdu, 2012: 1514-1519.

[4] Xing L D, Dai Y S. A New Decision-Diagram-Based Method for Efficient Analysis on Multistate Systems [J].IEEETransactionsonDependableandSecureComputing, 2009, 6(3): 161-175.

[5] Lisnianski A, Frenkel I. Recent Advances in System Reliability [M]. London: Springer-Verlag, 2012: 113-134.

[6] Borgonovo E, Apostolakis G E, Tarantola S,etal. Comparison of Global Sensitivity Analysis Techniques and Importance Measures in PSA [J].ReliabilityEngineeringandSystemSafety, 2003, 79(2): 175-185.

[7] Borgonovo E, Apostolakis G E.A New Importance Measure for Risk-Informed Decision Making [J].ReliabilityEngineeringandSystemSafety, 2001, 72(2): 193-212.

National Natural Science Foundation of China (No. 61164009); the Science and Technology Research Project, Department of Education of Jiangxi Province, China (No. GJJ14420); Natural Science Foundation of Jiangxi Province, China (No. 20132BAB206026)

1672-5220(2014)06-0789-04

Received date: 2014-08-08

* Correspondence should be addressed to GU ying-kui, E-mail: guyingkui@163.com

CLC number: X913.4 Document code: A