Periodical Inspections and Delay Replacement Model Based on Age Preventive Replacement Policy

WANG Wen-bin (王文彬), WANG Hui-ying (王慧颖), PENG Rui (彭 锐)

Dongling School of Economics and Management, University of Science and Technology Beijing, Beijing 100083, China

Periodical Inspections and Delay Replacement Model Based on Age Preventive Replacement Policy

WANG Wen-bin (王文彬), WANG Hui-ying (王慧颖)*, PENG Rui (彭 锐)

DonglingSchoolofEconomicsandManagement,UniversityofScienceandTechnologyBeijing,Beijing100083,China

Periodical inspections and an age-based preventive replacement (APR) model were proposed based on a two-stage failure process for a single component system. Inspection activities were performed at regular intervals. Once the system was identified to be at defective state by inspection, a maintenance decision needed to be made that whether to replace the defective system immediately or wait till the preset APR time. So a threshold was introduced into the model and called as inspection-based preventive replacement (IPR) threshold. If the distance from the defect identification point to the APR time was longer than the threshold, a preventive replacement (PR) action was made; otherwise PR action was to wait till the APR time. Two models were proposed and compared, and a numerical example was conducted to illustrate the applicability of the model.

delay-time;inspection;age-basedpreventivereplacement(APR);inspection-basedpreventivereplacement(IPR);preventivemaintenance(PM)

Introduction

For any preventive maintenance (PM) program, inspections are important maintenance activities. The aim of the inspection is to identify the system state and take necessary maintenance actions before failure. There have been many inspection models proposed in Refs.[1-5]. However, a class model using the delay-time concept stands out due to its concept clarity and close to inspection practice. Christer and Waller[6]first mentioned the concept of the delay-time. The concept defined the failure process as a two-stage failure process. The first stage was normal working stage from new to the point of a detectable defect arising. The second stage was defined as the failure delay time stage from this point onward to the failure if no other maintenance interventions were taken[6-7].

Age-based preventive replacement (APR) policy is a well-studied maintenance policy[8-12]. According to this policy, the system is replaced upon reaching the preset APR time or on failure whichever occurs first. Such preset APR time can be optimized with respect to the expected cost per unit time. However, most of models developed did not consider such policy in conjunction with inspections. In this paper, the proposed model considers the APR policy with periodical inspections. The idea in this paper is motivated by industrial observations. If the system is identified early to be in the failure delay-time stage, the system may need to be replaced immediately since one cannot wait for such a long time till the APR time to replace the system. However, if the system’s failure delay-time stage is identified at a time near to the APR time, it may delay replacement till the APR time. This leads to the determination of another decision variable which defines a distance till the APR time as a threshold to judge whether to wait or replace. Such a threshold is called the inspection-based preventive replacement (IPR) threshold. The mathematic model is established to optimize the expected cost per unit time in terms of the IPR threshold, the inspection interval, and the APR time.

1 Model Assumptions and Notations

1.1 Model assumptions

(1) A single component system is subjected to a single dominant failure mode.

(2) The process of the system failure can be broken down into two stages. Stage 1 represents the normal working stage,U, and Stage 2 represents the failure delay-time stage,H. The two stages are assumed to be independent.

(3) Inspection activities takes place at every time unitt, and then also occur at (A-τPR) (see Section 1.2). Inspections are perfect. Both the time spent on an inspection and the time for the APR are very short compared with the inspection and APR interval. Therefore they are negligible.

(4) If the status of the system is identified to be in the failure delay-time stage at some inspection points and the time till the APR time is greater than the IPR threshold, an IPR action needs to be taken immediately, otherwise the action needs to be delayed till the APR time.

(5) The system failures can be found immediately, and an identical item is used to substitute for the failed parts. IPR, APR, and failure replacement are regarded as renewing the system. So failure renewal, inspection-based renewal, and age-based renewal are three possible renewals in PM process of the system.

1.2 Notations

UTherandomdurationofStage1withprobabilitydensityfunc-tion(PDF)g(u)andcumulativedistributionfunction(CDF)G(u)HTherandomdurationofStage2withPDFf(h)andCDFF(h)τPRTheIPRthresholdtTheinspectionintervalATheAPRtimeCfAveragecostofafailurereplacementCpiAveragecostofanunplannedPRataninspection,wherepistandsforpreventivereplacementbasedoninspectionCpaAveragecostofaplannedPRatageA,andassumingCpi>Cpa,wherepastandsforpreventivereplacementbasedonageCiAveragecostofaninspectionE(C)ExpectedrenewalcyclecostE(L)ExpectedrenewalcyclelengthE(C/L)Expectedcostperunittime

The two models are established according to different inspection renewal policies. Model 1 presented in this paper assumes that the inspection renewal policy is performed according to assumption (4). In Model 2, the system is preventively replaced at the time of a first defect identification (no delayed PR at A)priortofailure.Defectidentificationmeansthatthesystemisidentifiedtobeinthefailuredelay-timestage.OtherassumptionsofModels1and2areidentical.

2 Model 1

2.1 Expected renewal cycle length

The expected renewal cycle length is the sum of three possible renewals,

E(L)=Ef(L)+Ep(L)+Ea(L),

(1)

where Ef(L) is the expected failure renewal time. When a failure occurs beforeA, there are three possible situations (see Fig.1).

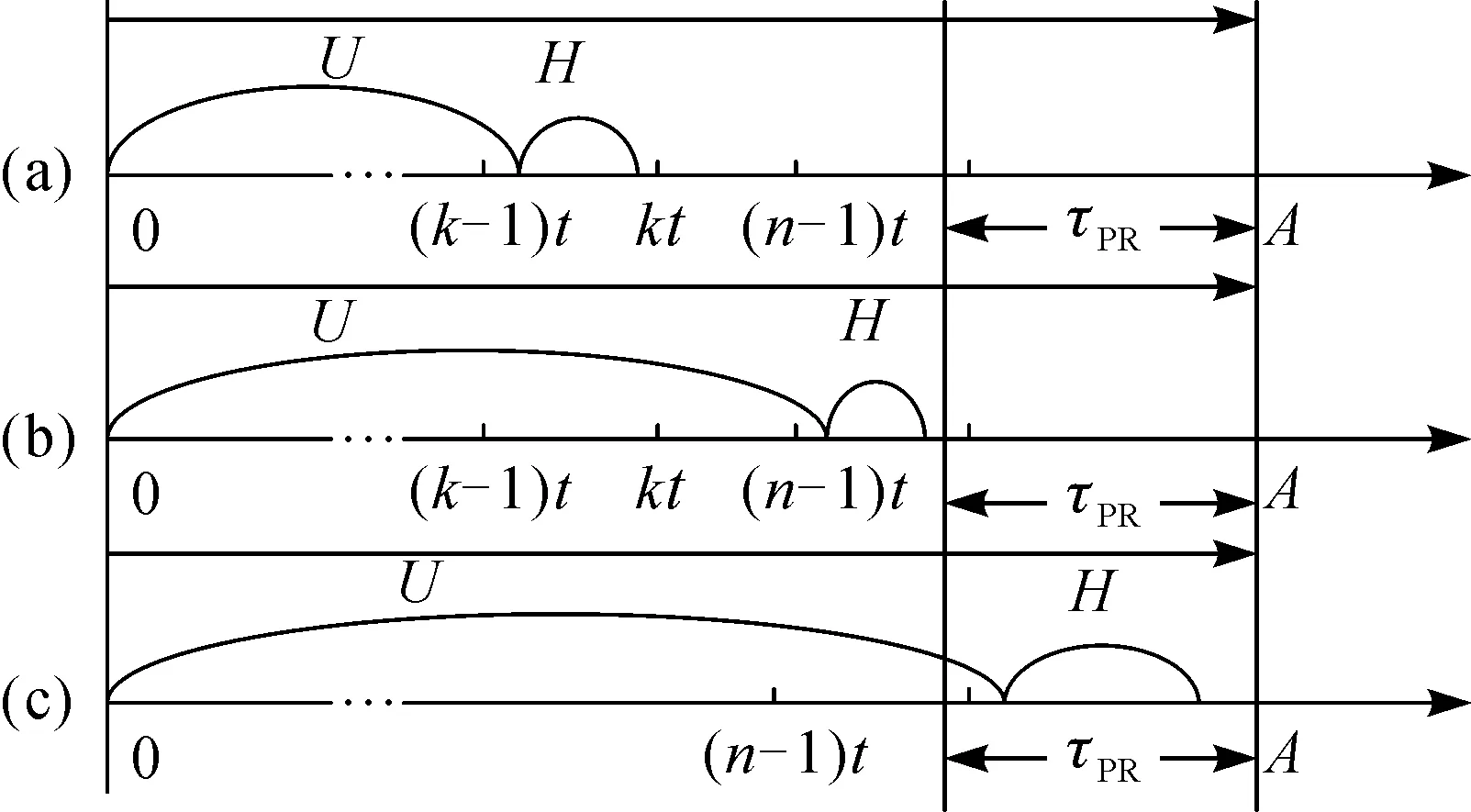
Fig.1 A failure’s occurrence in (a) ((k-1)t, kt),

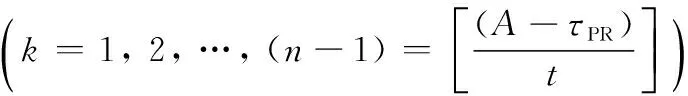
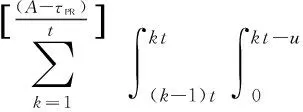
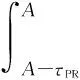
(2)

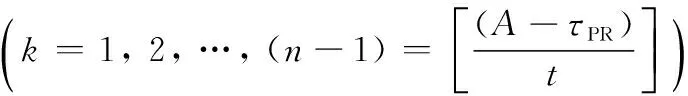
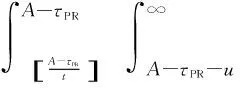
(3)

Ea(L) is the expected APR renewal time. It can only occur when either the system is still normal atAor the failure delay-time stage occurs after (A-τPR) but doesn’t fail yet atA.

A·[1-G(A)].

(4)

Summing Eqs. (2) - (4), we get

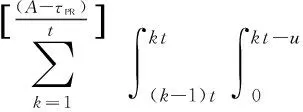
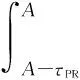
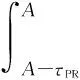
A·[1-G(A)].

(5)

2.2 Expected renewal cycle cost

Let E(C) denote the expected renewal cycle cost. Its derivation parallels those of Eqs. (1) - (4). Replace the time measures in Eq. (5) by the corresponding costs, so that

E(C) =Ef(C)+Ep(C)+Ea(C)=

g(u)f(h)dhdu+

g(u)f(h)dhdu+

Ci)·g(u)f(h)dhdu+

g(u)f(h)dhdu+

g(u)f(h)dhdu+

[1-G(A)].

(6)

2.3 Expected cost per unit time

The expected cost per unit time is considered as objective function to optimizet,τPR, andA. By using the renewal reward theorem[13], E(C) and E(L) need to be derived so that

(7)

3 Model 2

In this model,the system is preventively replaced at the time of a first defect identification (no consideration of the IPR threshold and a delayed PR strategy) prior to failure.

3.1 Expected renewal cycle length

As before,Model 2 also has the three kinds of renewals. Ef(L) is the expected time that a failure renewal occurs at ((k-1)t,kt) (k=1, 2, …,N=[A/t]), or ([A/t]t,A) before any defect is found at inspection points.

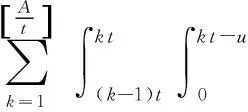
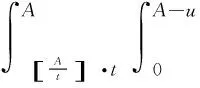
(8)

Ep(L) is the expected time that the system is renewed atktafter a defect is first found atkt(k=1, 2, …,N=[A/t]), so Ep(L) is formulated by

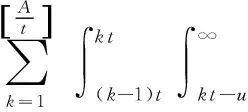
(9)

Ea(L) is the expected APR time which occurs atA. Two events lead to this renewal, which areUoccurred at ([A/t]t,A) and afterA. Summing up these two possibilities, Ea(L) can be obtained as follows.

A·(1-G(A)).

(10)

The expected renewal cycle length is the summation of Eqs. (8) - (10), and it is given by

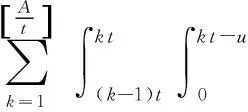
A·(1-G(A)).

(11)

3.2 Expected renewal cycle cost

Following the same way, the expected renewal cycle cost of Model 2 is given by

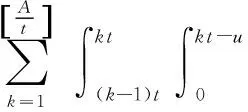
(12)

Equation (7) follows from Eqs. (11) and (12).tandAare regarded as the decision variables of Model 2.

4 Results and Discussion

Now a case is introduced based on the fitted parameters of the model used in Baker and Wang[14-15]. They used Weibull distribution for bothUandH. The parameter values are estimated using the maximum likelihood method based on history inspection and failure data. The estimated parameters are shown in Table 1, where exis exponential function, and e=2.71828. The estimates for cost parameters are shown in Table 2.

Table 1 Distributions of U and H and corresponding parameter

Table 2 Estimates of cost parameters (in US dollars)

The comparison results of Models 1 and 2 are shown in Fig. 2,i.e., the expected cost per unit time of Model 1 is lower than that of Model 2. For Model 2, optimal values areA*=11.8 months,t*=8.9 months, and E*(T) =0.265401. The volumetric infusion pump has a relatively longer APR time using Model 1. The hospital at the time checked the pump at an interval of 6 months[8]. To keep the expected cost per unit time down, no matter from which result of the two models, the inspection intervals of the pump should be extended. However, the recommendation of Model 1 is the most ideal one.

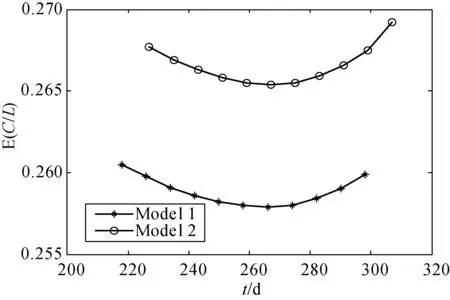
Fig.2 Comparison of Models 1 and 2 for the volumetric infusion

5 Conclusions

In this paper,the delay time model based on the two-stage failure process has been extended jointly considering periodical inspections and APR policy. The developed models are for the aim of PM scheduling and offer another maintenance decision, according to IPR threshold to judge whether to delay PR until APR or replace immediately. Two kinds of cost models are studied under the options. The numerical example clearly shows that Model 1 is better than Model 2 with the reasonable cost parameters and model structure.

[1] Wang W. An Inspection Model for a Process with Two Types of Inspections and Repairs [J].ReliabilityEngineeringandSystemSafety, 2009, 94(2): 526-533.

[2] Golmakani H R, Moakedi H.Periodic Inspection Optimization Model for a Multi-component Repairable System with Failure Interaction [J].TheInternationalJournalofAdvancedManufacturingTechnology, 2012, 61(1/2/3/4): 295-302.

[3] Cui L R, Xie M, Loh H T. Inspection Schemes for General Systems [J].IIETransactions, 2004, 36(9): 817-825.

[4] Taghipour S, Banjevic D, Jardine A K S. Periodic Iinspection Optimization Model for a Complex Repairable System [J].ReliabilityEngineeringandSystemSafety, 2010, 95(9): 944-952.

[5] Huynh K T, Berenguer C, Berenguer C,etal. A Periodic Inspection and Replacment Policy for Systems Subject to Competing Failure Modes due to Degradation and Traumatic Events[J].ReliabilityEngineering&SystemSafety, 2011, 96(4): 497-508.

[6] Christer A H, Waller W M.Reducing Production Downtime Using Delay-Time Analysis [J].JournaloftheOperationalResearchSociety, 1984, 35(6): 499-512.

[7] Wang W. An Inspection Model Based on a Three-Stage Failure Process [J].ReliabilityEngineeringandSystemSafety, 2011, 96(7): 838-848.

[8] Scarf P A, Cavalcante C, Dwight R A,etal. An Age-Based Inspection and Replacement Policy for Heterogeneous Components [J].IEEETransactionsonReliability, 2009, 58(4): 641-648.

[9] Castro I T, Barros A, Grall A. Age-Based Preventive Maintenance for Passive Components Submitted to Stress Corrosion Cracking [J].MathematicalandComputerModelling, 2011, 54(1): 598-609.

[10] EI-Ferik S. Economic Production Lot-Sizing for an Unreliable Machine under Imperfect Age-Based Maintenance Policy [J].EuropeanJournalofOperationalResearch, 2008, 186(1): 150-163.

[11] Huynh K T, Castro I T, Barros A,etal. Modeling Age-Based Maintenance Strategies with Minimal Repairs for Systems Subject to Competing Failure Modes due to Degradation and Shocks [J].EuropeanJournalofOperationalResearch, 2012, 218(1): 140-151.

[12] Chien Y H, Sheu S H. Extended Optimal Age-Replacement Policy with Minimal Repair of a System Subject to Shocks [J].EuropeanJournalofOperationalResearch, 2006, 174(1): 169-181.

[13] Ross S M. Introduction to Probability Models [M]. USA: Elsevier, 2007.

[14] Baker R D, Wang W.Estimating the Delay Time Distribution of Faults in Repairable Machinery from Failure Data [J].IMAJournalofMathematicsAppliedinBusinessandIndustry, 1991, 3(4): 259-281.

[15] Wang W. Delay Time Modelling [M]. //Murthay P, Kobbacy A. Complex System Maintenance Handbook. London: Springer, 2008: 345-370.

National Natural Science Foundation of China (NSFC) (No.71231001); China Postdoctoral Science Foundation Funded Project (No. 2013M530531); the Fundamental Research Funds for the Central Universities of China (Nos. FRF-MP-13-009A, FRF-TP-13-026A); the MOE PhD Supervisor Fund, China (No. 20120006110025)

1672-5220(2014)06-0744-03

Received date: 2014-08-08

* Correspondence should be addressed to WANG Hui-ying, E-mail: wanghuiying120454@163.com

CLC number: TB114.3 Document code: A