Reliability Analysis Based on a Nonlinear Fatigue Damage Accumulation Model

YUAN Rong (袁 容), LI Hai-qing (李海庆)

School of Mechanical Electronic and Industrial Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China

Reliability Analysis Based on a Nonlinear Fatigue Damage Accumulation Model

YUAN Rong (袁 容), LI Hai-qing (李海庆)*

SchoolofMechanicalElectronicandIndustrialEngineering,UniversityofElectronicScienceandTechnologyofChina,Chengdu611731,China

A modified nonlinear fatigue damage accumulation model based on the Manson-Halford theory was presented, and the new model was developed for fatigue life prediction under constant and variable amplitude loading, which took the effects of the load interactions and the phenomenon of material’s strength degradation into account. The experimental data of the 30CrMnSiA and the LY-12cz from literature were used to verify the proposed model. And from the good agreement between the experimental data and predicted results, we can see it clear that the proposed method can be applied to predicting fatigue life under different loadings.

fatiguedamageaccumulation;Manson-Halfordtheory;loadinteractions;strengthdegradation

Introduction

As is known to us, fatigue is a damage accumulation process and it is one of the main failure reasons for most of the mechanical components[1]. Thus, it is important to predict the reliability and the life of these components. In general, fatigue damage accumulation theory can be generally classified into two categories: linear damage accumulation and nonlinear damage accumulation theories. Though the linear damage accumulation theory, which is also called the Palmgreen-Miner rule (just Miner’s rule for short) has been widely used in engineering[2], it has some shortcomings such as it not only neglects the effects of loading sequence but also ignores the load interaction, which results in the disagreement between the predicted and experimental value. Accordingly, to remedy the drawbacks of Miner’s rule, there are lots of researchers concerning the nonlinear damage accumulation models: continuum damage mechanics models[3-4]; damage theories based on thermodynamic entropy[5-6]; damage theories based on physical property degradation[7-8]. However, there are still some issues needed to be improved for nonlinear damage accumulation model, such as considering the strength degradation of materials. Because the strength of a component degenerates gradually under cyclic loading, the residual life will be reduced with the increasing working time; and when the residual strength of a material is less than the stress loading, the failure happens.

To investigate the damage accumulation and the strength degradation, many studies have been done on this subject. Chou and Croman[9-10]used similar rate type differential equations to predict residual strength under a single stress level. Diaoetal.[11]predicted the residual strength under complex stress states and developed a generalized residual material property degradation model. Schaff and Davidson[12]focused on the strength-based model for predicting the residual strength and life of composite structures which subjected to constant amplitude and two-stress level loading conditions. More detail comments on these models can be found in Ref. [13].

In this paper, we developed a nonlinear damage accumulation model considering the effects of residual strength degradation and the effects of load interactions. The reminder of this paper is organized as follows. Section 1 introduces the residual strength degradation model, and a modified nonlinear fatigue damage accumulation considering the residual strength degradation is proposed in Section 2. The validation of the proposed model is processed in Section 3. And the reliability analysis using the proposed model is introduced in Section 4. Finally, Section 5 summarizes the paper and some conclusions are drawn.

1 The Residual Strength Degradation Model

Assume that the static strength degradation of material under constant amplitude loading can be calculated as[14]:

(1)

whereδR(n) is the residual strength of material,nis the number of loading cycles at a given stressσ,canddare dimensionless parameters which are relative to the environment conditions. In addition,δR(n) has the boundary condition as follows

δR(0)=δ(0),δR(N)=σ.

(2)

According to the theory of thermodynamics, fatigue damage accumulation is the irreversible energy dissipation process. Therefore, the residual strengthδR(n) should be a monotone decreasing function. And from Eq. (1), the proposed strength degradation model meets the irreversible condition since dδR(n)/dn<0.

Then integrating Eq. (1) and combining with Eq. (2), it can be easily obtained the following equation

(3)

For the residual strength degradation under the applied cyclic stress, whenn=N, Eq. (3) can be rewritten as

(4)

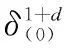
(5)

It is clear that Eq. (5) is the S-N curve. And using the available data ofσandN, the material parameterscandbcan be obtained by fitting S-N curve.

Similarly, if fatigue damage is caused by theklevel stress amplitude blocks, the residual strength degradation of material after applingnicycles atσican be obtained by

(6)

Based on the concepts and assumptions stated above, an expression for estimating the residual strength degradation afterklevel stress can be developed as

(7)

In order to calculate the residual strength degradation conveniently, a residual strength degradation coefficient is introduced as

(8)

When the fatigue damage is caused by theklevel stress, combining Eqs. (6) - (8), the residual strength degradation of a material underklevel stress can be obtained as

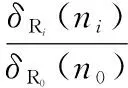
(9)

Substituting Eq. (7) into Eq. (9), we get the residual strength model, that is

(10)

2 A Modified Nonlinear Fatigue Damage Accumulation Model

(11)

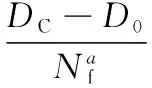
(12)

Then, substituting Eq. (12) into Eq. (11) leads to

(13)

Assume that no initial damage has occurred and damage failure occurs whenDC=1. Thus, Eq. (13) can be rewritten as

(14)

(15)

Therefore, we can calculate the damage accumulation for the two-stress level loading. Firstly, we assume the specimen is loaded at stressσ1forn1cycles, and then at stressσ2forn2cycles up to failure. To make use of equivalence of damage for different loading conditions, it is possible to establish an equivalent number of cyclesneffapplied with stress amplitudeσ2, which is equal to the amount of damage caused byn1cycles atσ1. Thus, according to the modified Manson-Halford model, the effective number of cycles can be determined from Eq. (16) and given by

(16)

Therefore, the total damage afterneff+n2cycles atσ2turns into

(17)

Then the damage accumulation model under two-stress level loading can be described as

(18)

(19)

Then fatigue cumulative damage under high-low loading sequence is as follows.

(20)

Similarly, for high-low loading conditions, the cumulative damage is less than unit. In the same way, it may be proven, for low-high loading conditions, the cumulative damage is more than unit. For the same two-stress level loading, there is no loading interaction effect, anda=1. Equation (18) can be reduced to the Miner’s rule

(21)

From the discussion above, we can see that the modified damage accumulation model is reasonable. Furthermore, if we take the strength degradation into account, the damage induced by theniapplied cycles atσiis

(22)

3 Experimental Verifications of the Proposed Model

In order to verify the descriptive ability of Eq. (22), the experimental data of 30CrMnSiA were used to verify the proposed model[16]. The material constants arec=19.32,d=15.59, andα=0.425; the two-stress level loadings areσ1=836 MPa andσ2=732 MPa, and their cycles to failure areNf1=7204 andNf2=55762, respectively; the high-low load spectrum was 836-732 MPa and low-high load spectrum was 732-836 MPa. The results of 30CrMnSiA between experiment and prediction are listed in Table 1.

Table 1 The experiment and prediction comparison of different models

From the results, we can see that the proposed model has better life prediction capabilities than the conventional model. Meanwhile, it is clear that the fatigue accumulative damage predicted by the proposed model exceeds unity when the load sequence is low-high loading sequence, and the damage value is less than unity for the high-low loading conditions, which demonstrates the effect of residual strength degradation and the loading interaction.

4 The Reliability Analysis Using the Proposed Model

According to the stress-strength interference model, the component is reliable, when the loading stress is less than the residual strength, and the reliability is equal to all the sum of the probability that the loading stress is less than the residual strength, that is

(23)

For convenience, we assume the residual strength follows the lognormal distribution. Then, the reliability of a component can be obtained, as follows

(24)

We employed the data of the LY-12cz[17]to illustrate the reliability analysis of the proposed method. The expectation and variance of the residual strength isμ=5.877 andσ0=0.215, respectively. Therefore, the results of fatigue reliability obtained from Eq. (24) are shown in Fig.1.

Fig.1 The reliability analysis of a component under constant amplitude loading

From the results, we can see it clearly that there are good agreements between the prediction results by the proposed method and the experimental data.

5 Conclusions

In this paper, a modified nonlinear fatigue damage accumulation model considering the residual strength degradation is developed. And it has a good characterization of fatigue damage evolution over the conventional model, because it considers the effects of load interaction, loading history, and strength degradation in materials. In order to validate and verify the proposed model, the experimental data from the literature are used, and from the comparison between the experimental data and the predicted results, we can see it has a good agreement, which indicates that the proposed model can describe the fatigue damage accumulation very well.

[1] Marco S M, Starvey W L. A Concept of Fatigue Damage[J].TransactionsoftheASME, 1954, 76(4): 627-632.

[2] Miner M A. Cumulative Damage in Fatigue[J].JournalofAppliedMechanics,1945, 12(3): 159-164.

[3] Besson J. Continuum Models of Ductile Fracture: a Review[J].InternationalJournalofDamageMechanics, 2010, 19(1): 3-52.

[4] Yuan R, Li H Q, Huang H Z,etal. A New Non-Linear Continuum Damage Mechanics Model for Fatigue Life Prediction under Variable Loading[J].Mechanika, 2013, 19(5): 506-511.

[5] Risitano A, Risitano G. Cumulative Damage Evaluation of Steel Using Infrared Thermography[J].TheoreticalandAppliedFractureMechanics, 2010, 54(2): 82-90.

[6] Naderi M, Amiri M, Khonsari M M. On the Thermodynamic Entropy of Fatigue Fracture[C]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, London, UK, 2010: 423-438.

[7] Ye D Y, Wang Z L. A New Approach to Low-Cycle Fatigue Damage Based on Exhaustion of Static Toughness and Dissipation of Cyclic Plastic Strain Energy during Fatigue[J].InternationalJournalofFatigue, 2001, 23(8): 679-687.

[8] Cheng G X, Plumtree A. A Fatigue Damage Accumulation Model Based on Continuum Damage Mechanics and Ductility Exhaustion[J].InternationalJournalofFatigue, 1998, 20(7): 495-501.

[9] Chou P C, Croman R. Residual Strength in Fatigue Based on the Strength-Life Equal Rank Assumption[J].JournalofCompositeMaterials, 1978, 12(2): 177-194.

[10] Chou P C, Croman R. Degradation and Sudden Death Models of Fatigue of Graphite/Epoxy Composites[C]. Composite Materials: Testing and Design (5th Conference) ASTM STP674, New Orleans, USA, 1979: 431-454.

[11] Diao X X, Lessard L B, Shokrieh M M. Statistical Model for Multiaxial Fatigue Behavior of Unidirectional Plies[J].CompositesScienceandTechnology, 1999, 59(13): 2025-2035.

[12] Schaff J R, Davidson B D. Life Prediction Methodology for Composite Structures. Part I — Constant Amplitude and Two Stress Level Fatigue[J].JournalofCompositeMaterials, 1997, 31(2): 128-157.

[13] Philippidis T P, Passipoularidis V A. Residual Strength after Fatigue in Composites: Theory vs. Experiment[J].InternationalJournalofFatigue, 2007, 29(12): 2104-2116.

[14] Lu W G, Xie L Y, Xu H. A Nonlinear Model of Strength Degradation[J].JournalofMechanicalStrength, 1997, 19(2): 55-62.(in Chinese)

[15] Xu J, Sheng D G, Sun G Q,etal. Fatigue Life Prediction for GH4169 Superalloy under Multiaxial Variable Amplitude Loading[J].JournalofBeijingUniversityofTechnology, 2012, 38(10): 1462-1466. (in Chinese)

[16] Fang Y Q, Hu M M, Luo Y L. New Continuous Fatigue Damage Model Based on Whole Damage Field Measurements[J].JournalofMechanicalStrength, 2006, 28(4): 582-596. (in Chinese)

[17] Guo S G, Yao W X. Reliability Model for Structural Elements Based on Fatigue Residual Life[J].JournalofNanjingUniversityofAeronautics&Astronautics, 2003, 35(1): 25-29. (in Chinese)

National Natural Science Foundation of China (No. 11272082); Fundamental Research Funds for the Central Universities (No. E022050205); the Open Research Fund of Key Laboratory of Fluid and Power Machinery of XiHua University, China (No. szjj2013-03)

1672-5220(2014)06-0741-03

Received date: 2014-08-08

* Correspondence should be addressed to LI Hai-qing, E-mail: lihaiqing27@uestc.edu.cn

CLC number: TG405 Document code: A