带移动滑块的太阳帆航天器动力学建模与姿态控制*

张震亚 韩艳铧 贾 杰

1. 南京航空航天大学航天学院，南京210016 2. 南昌航空大学信息工程学院，南昌330063



带移动滑块的太阳帆航天器动力学建模与姿态控制*

张震亚1韩艳铧1贾 杰2

1. 南京航空航天大学航天学院，南京210016 2. 南昌航空大学信息工程学院，南昌330063

针对以移动滑块为控制执行机构的太阳帆航天器，基于拉格朗日分析力学建立了航天器—滑块两体系统非线性耦合动力学模型。为简化控制律设计，将控制回路分为内外环，并分别设计控制律。外环以航天器姿态为受控变量，滑块位移为控制输入；内环以滑块位移为受控变量，滑块驱动力为控制输入。最终将控制律代入系统原非线性模型，以行星际太阳帆航天器姿态控制任务为例进行数值仿真。仿真结果表明，以移动滑块为执行机构，采用所设计控制律，可以实现太阳帆航天器快速姿态调整及长期姿态保持。

太阳帆；姿态控制；动力学建模；移动滑块

太阳帆航天器以太阳光压作为推进力进行飞行。作为一种采用全新推进方式的航天器，由于其无需消耗大量燃料即可在太阳光压持续推进下达到很高的速度，因而成为近年来航天领域的研究热点。

太阳帆具有质量轻，体积巨大的结构特点，其自身转动惯量较大。限于制造装配工艺水平，太阳帆航天器质心往往不与光压压心重合，因此,光压会对太阳帆产生比普通航天器大得多的姿态干扰力矩。若采用传统的姿控执行机构，如动量轮系统或化学燃料推进器等对太阳帆的姿态进行控制，则需要消耗大量的能量或燃料[1]。因此，针对太阳帆航天器，必须设计新型的高效率、无化学推进剂消耗的姿控系统。

目前研究中的太阳帆航天器姿态控制方案主要有质心偏移法和帆面转动法。前者通过使太阳帆的质心相对压心的位置产生偏离，得到光压姿态控制力矩。执行机构可以是带万向节的转动控制杆，或是沿帆面结构杆滑动的质量块等；后者则通过改变整体帆面或部分帆面的方向来产生光压控制力矩。

本文研究了基于移动滑块的太阳帆航天器姿态控制方案，与主流的采用控制杆或控制翼面的控制方案相比，该方案保证了有效载荷与帆面的相对位置固定，有利于航天器实现定向观测和对地稳定通信[2]，且执行机构的物理结构简单，易于实现，可靠性高，对帆面展开过程不造成干扰，能够满足太阳帆航天器快速姿态机动的任务要求[3-5]。

本文以太阳帆航天器偏航通道为例，建立其姿态动力学模型；将姿态控制系统分解为外环和内环系统，并分别进行控制律设计；最后通过数值仿真验证所设计姿态控制律的有效性。

1 系统动力学建模

带移动滑块的太阳帆航天器结构如图1所示。

图1 太阳帆航天器物理结构

其姿态控制基本原理为：在太阳帆航天器的4根结构杆上装配有可沿杆作受控滑动的质量块；理想初始状态下，太阳帆质心与太阳光压压心重合，此时太阳光压对航天器无力矩作用，通过调整滑块位置可改变系统质心位置，从而使系统质心位置偏离光压压心，产生所需光压姿态控制力矩。

为简化建模过程，这里将沿着同对角线两根结构杆滑动的双滑块等效为可沿全对角线移动的单滑块进行处理。

1.1 坐标系和符号定义

建立惯性坐标系oxy，原点o为空间某一固定点，x轴与太阳光方向垂直，y轴正方向与太阳光单位矢量S相反；建立与太阳帆航天器固连的体坐标系osxsys，原点os取在太阳帆本体质心处，2坐标轴分别指向太阳帆帆面切向与法向方向，如图2所示。

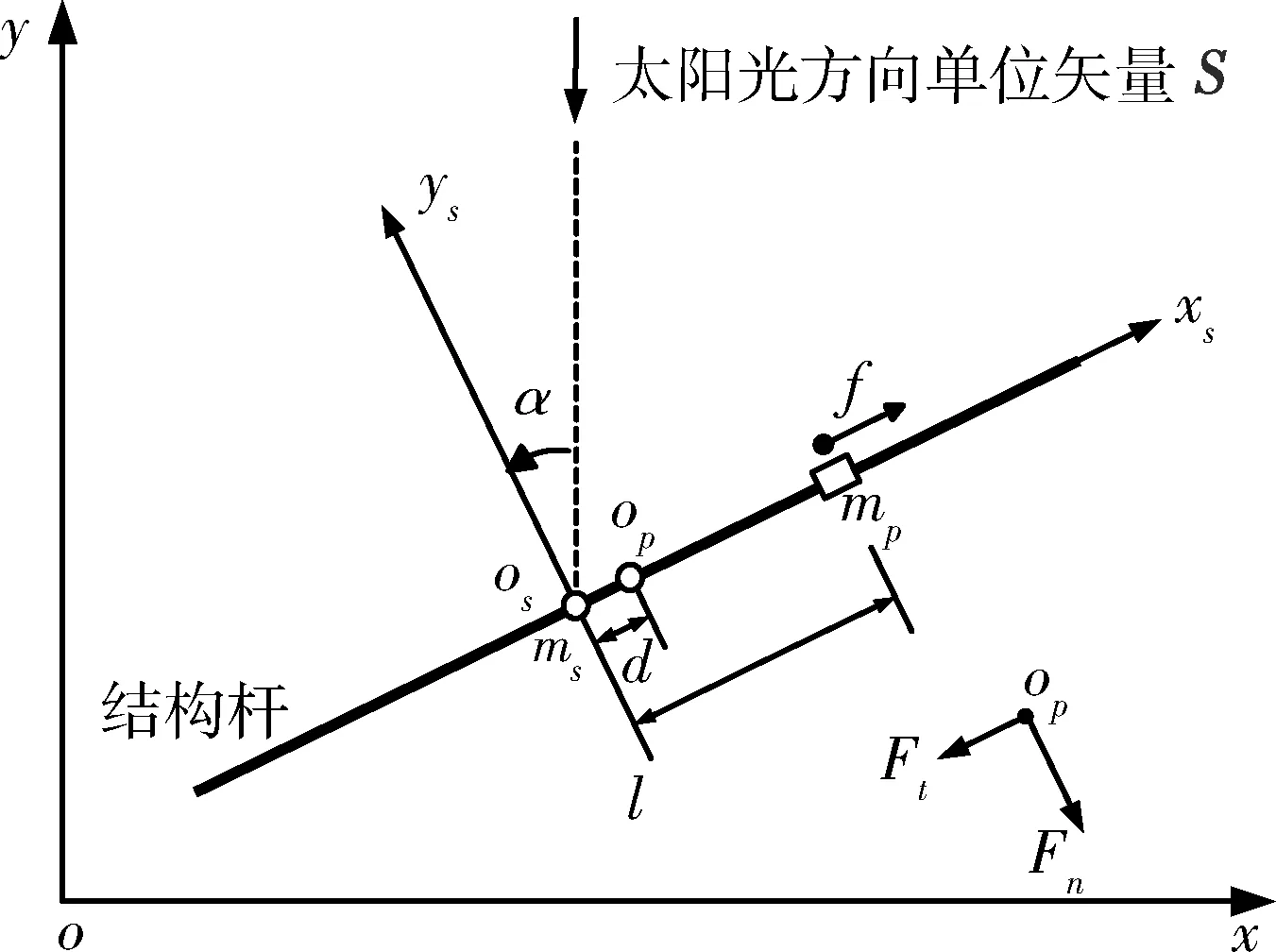
图2 太阳帆航天器偏航轴简化结构图

定义帆面法向与y轴夹角为偏航姿态角α，为保证帆面正面指向太阳，姿态角机动范围限制为(-90°,90°)；太阳帆本体质量为ms，本体关于偏航轴的转动惯量为Js；移动滑块质量为mp，视其为质点，忽略其自身转动惯量；滑块由电机驱动，沿帆面对角线结构杆作可控滑动，所受到的控制驱动力为f，方向沿结构杆；滑块在导轨上的位移为l，忽略滑块与导轨接触面间的摩擦力。

由于太阳帆实际制造装配误差，太阳帆本体质心os与光压压心op并不重合，质心与压心间存在偏差小量d。

1.2 太阳光压模型

太阳光压模型可表示为如下形式[6]：

F=PAUAcosα[(1+ρscos2α)S+ρssin2αS⊥]

(1)

其中，PAU为距离太阳一个天文单位处太阳光压大小，A为帆面面积，ρs为太阳帆镜面反射系数，S⊥为垂直太阳光方向的单位矢量。定义Fs，F⊥为太阳光压力沿S和S⊥方向的分量，则有：

Fs=PAUAcosα(1+ρscos2α)

(2)

F⊥=PAUAρssin2αcosα

(3)

考虑太阳帆的光学和热力学特性，可以得到太阳光压力沿太阳帆帆面切向和帆面法向分量Ft和Fn(如图2)的表达式[6]：

Ft=PAUA(1-rρs)sinαcosα

(4)

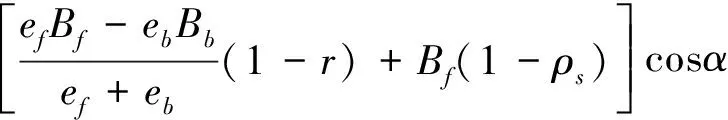
(5)

其中，Bf,Bb分别为太阳帆正面和背面的非朗伯系数，ef,eb分别为太阳帆正面和背面的发射系数，r为太阳帆正面反射率。

1.3 动力学模型推导

滑块位置矢量为：

(6)

则滑块速度矢量为：

(7)

设太阳帆航天器系统总动能为T，太阳帆本体动能为Ts，滑块动能为Tp，有：

(8)

(9)

系统总动能可表示为：

T=Ts+Tp

(10)

忽略太阳帆弹性形变，则航天器系统势能U=0。

定义广义坐标q=[α,l,X,Y]T，广义力Q=[Q1,Q2,Q3,Q4]T，由虚功原理，求得广义力表达式为：

Q1=-Fnd

(11)

Q2=f

(12)

Q3=-Ftcosα+Fnsinα

(13)

Q4=-Ftsinα-Fncosα

(14)

将广义力Q及拉格朗日函数L=T-U代入拉格朗日动力学方程：

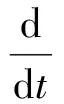
(15)

得太阳帆航天器-滑块两体系统耦合动力学模型：

(16)

(17)

(18)

(19)

由式(16)～(19)消去变量x，y，整理得

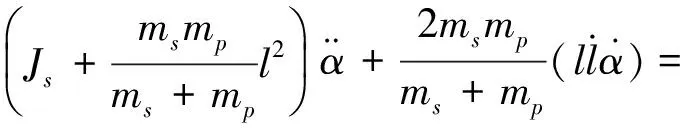
(20)

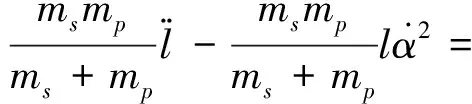
(21)

将式(20)和(21)代入光压模型式(4)和(5)，并定义如下常参数：

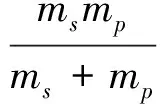
最终得到太阳帆航天器偏航通道姿态动力学方程为：

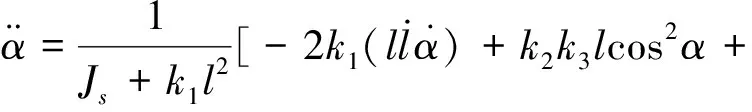
(22)

(23)

2 姿态控制器设计

式(22)和(23)显示受控系统是一个四阶非线性耦合不确定系统。如果直接以滑块驱动力f作为控制输入来控制航天器姿态角，控制律的设计将比较困难，且难以在后续环节进行执行机构的分配策略设计；而若将控制回路分为内外环分别设计控制器，外环以航天器姿态为受控变量，滑块位移为控制输入；内环以滑块位移为受控变量，滑块驱动力为控制输入，则可望显著降低控制律设计的复杂度。控制系统设计思想如图3所示。

图3 太阳帆航天器姿态控制系统结构图

2.1 外环姿态控制器设计

(24)

式(24)即为外环系统动力学方程。

定义姿态跟踪误差Δαα-αc，其中αc为偏航姿态指令。将Δα代入式(24)，可得关于Δα的方程：

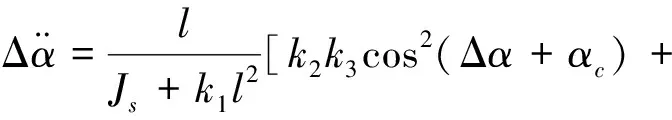
(25)

将式(25)在平衡点Δα=0,l=0处进行小扰动线性化，可得到关于Δα的线性方程：

(26)

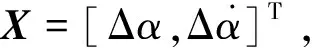
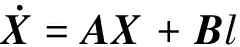
(27)

其中：

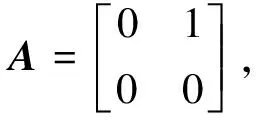
对于目标姿态指令αc已经确定的任意一次任务来说，所得系统式(27)为线性定常，针对该线性系统设计LQR控制器，定义性能指标：

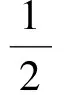
(28)

其中，Q为2×2正定对称常数矩阵，R为正常数。由线性二次型最优控制理论，得到：

l*=-R-1BTP·X(t)

(29)

其中,P满足代数黎卡提方程：

PA+ATP-PBR-1BTP+Q=0

(30)

通过式(30)求解P，最终可得最优控制输入l*。

(31)

2.2 内环姿态控制器设计

以外环控制器给出的滑块最优控制位移l*作为内环回路跟踪指令lc，滑块实际位移l作为受控变量，驱动力f作为控制输入，设计内环控制律。滑块动力学方程如式(23)，定义跟踪指令位移lc，跟踪误差Δll-lc，构建滑块位置误差Δl的理想动态：

(32)

通过对式(32)配置合适的控制参数c1,c2，可使滑块位置误差Δl→0，即l→lc。

将Δl=l-lc代入式(32)，与式(23)联立整理，可得：

(33)

2.3 系统完整姿态控制律

系统外环和内环控制律分别由式(29)和(33)给出，其中式(33)中内环跟踪目标位移lc即为外环控制律式(29)得到的最优输入位移l*。

考虑到外环给出滑块最优输入位移l*已经过限幅处理，为保证内环实际输出的滑块位移幅值不超过最优输入位移指令，应选择合适的控制参数c1,c2，使内环系统保持在过阻尼状态。

将式(29)代入式(33)，可得到系统完整姿态控制律：

(34)

由于滑块驱动机构的性能限制，滑块在沿导轨作受控运动时，施加驱动力大小需限制在一定范围内。定义滑块驱动力最大绝对值为fmax，限幅处理后滑块驱动力为flim，设计滑块驱动力限幅器如下：

(35)

3 执行机构分配策略

为了简化姿态动力学建模过程，本文将沿着对角线两根导轨各自运动的双滑块等效为可沿太阳帆全对角线运动的单个滑块，并对单滑块进行控制律设计。而在工程实现过程中，需将设计的单滑块控制律还原为双滑块控制律，即把单个滑块的受控运动分配到运动位移分别恒正/恒负的双滑块上。

由于滑块实际运动过程中存在电机驱动噪声和摩擦力，必然对航天器系统动态引入一定干扰。为减少滑块运动过程对航天器动态可能造成的不良影响，采用如下运动分配策略：

l1=[sgn(l)+1]·l,l2=[sgn(l)-1]·l

(36)

其中，l为等效单滑块的位移；l1为沿正向导轨运动滑块的位移，l1≥0；l2为沿负向导轨运动滑块的位移，l2≤0。采用上述执行机构分配策略，可保证任一时刻同对角线上仅有一个滑块运动，尽可能减少滑块运动对系统动态的干扰。

4 数值仿真

针对上文建立的太阳帆航天器偏航通道姿态控制系统进行数值仿真。太阳帆航天器有关参数源自美国新千年计划ST7(New Millennium Program Space Technology 7, NMP ST7)的太阳帆实验任务[7]。具体仿真参数如表1所示。

表1 太阳帆航天器数值仿真参数

4.1 自由状态短期响应测试

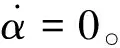
未施加姿态控制时，移动滑块锁定于0位移处。由于帆面质心与压心存在装配误差偏距d，使得航天器受到持续的光压干扰力矩。太阳帆姿态呈现出周期性振荡，且姿态角α无法保持在(-90°,90°)范围内，即无法保证帆面正面指向太阳(仿真过程中假定太阳帆正反面光反射条件相同)。其姿态角变化及所受干扰力矩变化如图4所示。

4.2 行星际太阳帆航天器姿态控制仿真

以行星际太阳帆航天器为例进行姿态控制系统数值仿真。

太阳光压模型式(2)和(3)给出了光压作用力沿太阳光方向及垂直太阳光方向的分量Fs，F⊥。对于图5所示的日心轨道太阳帆航天器而言，太阳光压力分量F⊥可作为轨道机动的有效推进控制力。

为使该轨道机动推力最大，可由式(37)求得所需姿态角α：

(37)

图4 自由状态下太阳帆航天器姿态变化及干扰力矩变化曲线

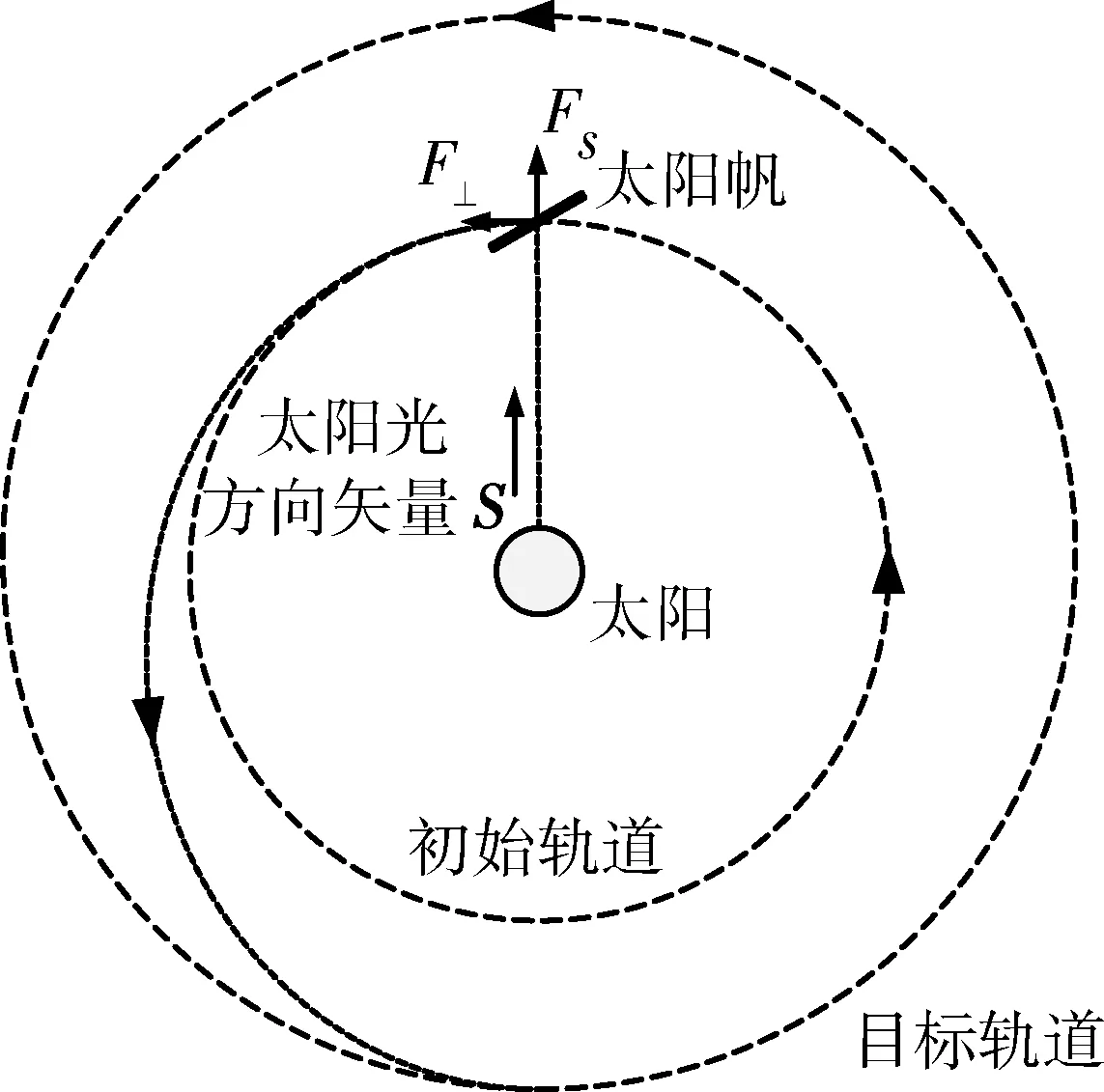
图5 行星际太阳帆航天器变轨示意图

最大。因此，对于往太阳系外部飞行的日心轨道行星际太阳帆航天器而言，任务设计时通常取α=35°作为变轨阶段的理想偏航角[6]。

仿真过程取内环控制器参数c1=60，c2=10，外环控制器参数Q=diag(103,103)，R=10，驱动力限幅fmax=10N，滑块位移限幅lmax=28m。仿真得到太阳帆航天器状态变化情况如图6，图7～8给出了姿控过程中滑块状态及驱动力变化曲线。

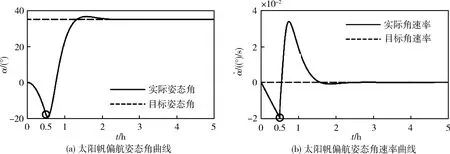
图6 太阳帆航天器姿态变化曲线

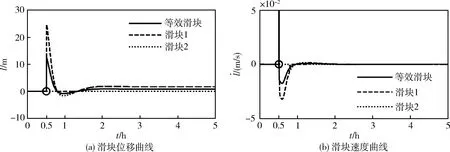
图7 滑块状态变化曲线

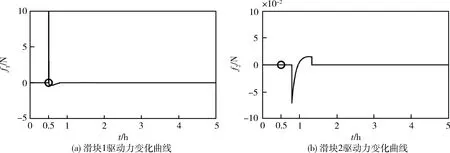
图8 滑块驱动力变化曲线

仿真结果表明，基于移动滑块的太阳帆航天器姿态控制方案具有良好的姿态控制效果，所设计控制律能针对存在初始角位置误差和角速度误差的太阳帆航天器进行有效的姿态控制，实现短时间内的较大角度姿态调整，同时可满足长期飞行任务中对干扰力矩抑制和姿态稳定的需求。

5 结论

研究结果表明，基于移动滑块的太阳帆航天器姿态控制方案，能够实现太阳帆航天器快速姿态调整及长期姿态稳定。针对外环姿控系统和内环驱动系统分别进行控制器设计，可以根据不同情况各自调节内外环控制参数，以满足实际太阳帆任务需求。

与传统带有控制杆或控制翼面的太阳帆姿态控制方案相比，基于移动滑块的太阳帆航天器姿态控制方案具有结构简单可靠，任务适应性强等特点，在太阳帆航天器技术领域有重要研究价值。

[1] McInnes C R. Solar Sailing: Technology, Dynamics and Mission Applications[M]. Springer, 2004.

[2] 罗超, 郑建华.采用滑块和 RSB 的太阳帆姿态控制[J].哈尔滨工业大学学报, 2011, 43(3): 95-101. (Luo Chao，Zheng Jianhua.Solar-sail Attitude Control Based on Moving Masses and Roll Stabilizer Bars[J]. Journal of Harbin Institute of Technology, 2011, 43(3): 95-101.)

[3] Murphy D M, Murphey T W, Gierow P A. Scalable Solar-sail Subsystem Design Concept[J]. Journal of Spacecraft and Rockets, 2003, 40(4): 539-547.

[4] Wie B. Thrust Vector Control Analysis and Design for Solar-sail Spacecraft[J]. Journal of Spacecraft and Rockets, 2007, 44(3): 545-557.

[5] Thomas S, Paluszek M, Wie B, et al. AOCS Performance and Stability Validation for Large Flexible Solar Sail Spacecraft[C].41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, 2005: 1-18.

[6] Wie B. Solar Sail Attitude Control and Dynamics, Part 1[J].Journal of Guidance, Control, and Dynamics, 2004, 27(4): 526-535.

[7] Wie B. Solar Sail Attitude Control and Dynamics, Part 2[J].Journal of guidance, Control, and Dynamics, 2004, 27(4): 536-544.

DynamicsModelingandAttitudeControlofMoving-MassBasedSolarSailSpacecraft

ZHANG Zhenya1HAN Yanhua1JIA Jie2
1. Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China 2. Nanchang Hangkong University，Nanchang 330063, China

TheSolarsailspacecraftwhichemploysmoving-masssystemisstudiedaboutinthispaper.ThenonlinearcouplingdynamicsmodelofSolarsailmoving-masstwo-bodysystemisestablishedbyusingLagrange’sequations．Inordertosimplifythedesignofcontrollaw,thecontrolloopisdividedintoouter-loopandinner-loopandattitudecontrollersforbothouter-loopandinner-looparedesigned.Theouter-loopchoosesattitudeangleandvelocityasstatevariablesanddisplacementofmoving-massascontrolinput,whiletheinner-loopchoosesdisplacementofmovingmassasstatevariableanddrivingforceascontrolinput.Thesimulationresultsshowthatthemoving-massbasedattitudecontrolsystembyusingthedesignedcontrollawhasgoodperformanceonsolarsail’slargeangleattitudemaneuveringandattitudekeeping.

Solarsail;Attitudecontrol;Dynamicmodeling;Moving-mass

*国家自然科学基金(61263012)

2013-06-25

张震亚(1989-)，男，硕士研究生，浙江嵊州人，主要研究方向为太阳帆航天器姿态动力学与控制；韩艳铧(1976-)，男，山西吕梁人，博士，副教授，硕士生导师，主要研究方向为挠性多体复杂航天器动力学与控制；贾杰(1972-)，男，河南新乡人，博士，副教授，硕士生导师，主要研究方向为飞行器制导与控制、非线性系统建模与故障检测。

V412. 4

： A

1006-3242(2014)05-0029-07