深大基坑中水平支撑的温度内力与变形计算★

范 君 宇

(上海强劲地基工程股份有限公司,上海 200233)

·岩土工程·地基基础·

深大基坑中水平支撑的温度内力与变形计算★

范 君 宇

(上海强劲地基工程股份有限公司,上海 200233)

以深大基坑支护结构为研究对象，建立了深大基坑水平支撑温度内力与变形的计算方法，通过计算结果与现场实测结果的比较，验证了所建立的温度内力与变形计算方法是可靠的，可供深大基坑的内支撑设计时参考，从而也证明了深大基坑中内支撑的内力可调是控制基坑变形和保证安全的有效方法。

深基坑，多层土，Winkler模型，温度内力

0 引言

随着我国经济水平和城市建设的迅速发展，深大基坑工程的数量越来越多。在深大基坑工程中,温度变化会影响支护结构中支撑的内力和变形,基坑设计规范[1]规定设计基坑内支撑体系时应考虑温度变化的影响,但是并没有提供相应的计算方法。深大基坑的水平支撑内力监测结果表明，温度变化30 ℃时，其120 m支撑内力增量达600 kN,从而说明深大基坑水平支撑的温度内力对基坑的安全影响是不可忽略的。

目前关于深基坑水平支撑温度应力的研究还比较少，并且这方面的研究也不是很完善。陆培毅等[2]在采用有限元方法模拟基坑开挖过程中支护结构与土的相互作用的基础上提出将温度场耦合到应力场中来,以分析基坑支护支撑的温度效应。 郑刚和顾晓鲁[3]基于弹性抗力法,提出单层支撑基坑温度应力的简化计算方法,该法计算简单,概念明确,可以考虑支撑—围护桩—土的相互作用。吴明等[4]在郑刚和顾晓鲁方法的基础上,推导出可以考虑多层支撑温度应力的计算方法。

上述计算方法中，均是假设围护墙后的土体的刚度都是相等的，即只考虑单层土的影响，而实际上基坑围护墙体后分布有多层土体，且性能相差较大。本文在结合实际工程情况的基础上，考虑围护墙后的土体的刚度随着不同土层i的变化，进一步分析围护墙后土体的分布和土层的性能对支撑温度内力的影响，建立了多道水平支撑下温度内力的计算方法，并分析了影响其温度内力变化的主要因素。

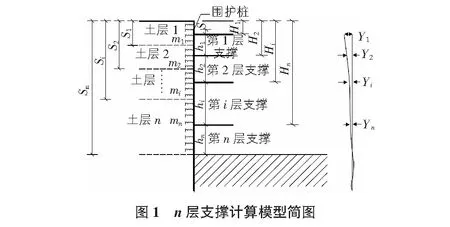
1 计算模型

方便计算，可作以下假设:1)围护桩因为支撑温度轴力变化产生的水平位移与相应围护桩后土体的变形协调,所以整个系统可以认为处于弹性变形状态；2)温度引起的支撑伸长和缩短与围护桩后土体的弹性变形相互协调,并取决于围护桩刚度和土体刚度的共同影响，土体的刚度随着不同土层变化;3)协调基坑支撑变形的桩后土的水平范围为D；4)支撑温度变化ΔT瞬间完成,支撑简化为一维杆件；5)围护桩后土体符合Winkler地基模型；6)假设协调第i层支撑水平位移的桩后土体竖向范围为Hi,hi为第i层与第i+1层支撑的间距；7)如果围护桩桩顶高程比第1层支撑高程高，则模型积分时可以不考虑。因为考虑该段使得积分结果比较冗繁,而且经过试算对精度提高不大,故不予考虑[4]。

n层支撑基坑的模型如图1所示,按照以上假设,对于第i层支撑,建立局部坐标系,如图2所示。

假设围护结构水平位移方程：

(1)

图2中对于hi中微小段dx有dF=kydx，则：

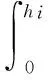
(2)

其中：

k=k1+k2=m(x+Hi)+k2

(3)

其中，k1为土体刚度，kN/m3；m为土体基床水平抗力系数的比例系数，kN/m4；对于围护桩，假设围护桩底为固定端，则其刚度为k2。

将式(1)、式(3)代入式(2)得：

(4)

假设协调基坑支撑变形的桩后土的水平范围为D，则第i层支撑轴力为：

N0=DF

(5)

积分式(5)得：

(6)

对第n层支撑，通过式(1)～式(5)的过程有：

(7)

同样采用Nn=DF，积分式(7)得:

(8)

变换得到：

(9)

温度变化引起支撑轴力变化，进而轴力变化又影响围护桩和围护桩后土体的弹性变形。同样的道理，土体的弹性变形反过来影响支撑变形。通过下面的流程进行迭代，反映以上土和支撑协调变形的过程，最终达到平衡。

(10)

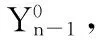
2 工程实例

2.1 杭州101地块

杭州101地块位于杭州市江干区章家坝，艮山西路南侧，运河东路东侧。基坑围护结构设置两道钢支撑，且围护墙形式为φ850@600三轴搅拌桩，L=19.1m，水泥掺量22%，压顶梁1 500×400，梁顶标高为-2.20m，内插H700×300×13×24型钢，L=12.1m，现场工程如图3所示。

由本文建立的模型可知，基坑深度9.1m，h1=2.4m，H1=1.8m，h2=4.9m，H2=4.2m，m1=5 480kN/m4，m2=6 000kN/m4，工法桩刚度K=k2hnD=10MN/m，对撑分担的基坑周边长度为D=40m，支撑长度L=92.3m，支撑横截面积A=0.017 189m2，α=12×10-6，钢支撑的弹性模量E=2.06×108kN/m2，N0=α·φ·ΔT·A·E，φ=0.4，N0=17.0kN,计算结果如表1,表2所示。

本工程中采用自动监测系统，在钢结构支撑中实现24h连续测量温度和钢结构的轴向内力，第一、第二道支撑实测的内力与温度的变化关系如图4，图5所示。实测得在单位温度下，第一道钢支撑轴力变化为15.0kN～16.0kN，第二道钢支撑轴力变化为16.5kN～17.5kN，计算结果与实测的相近，约相差5%，所以建立的计算方法是基本合适的，能满足工程设计需要。

表1 第二道支撑计算结果(一)

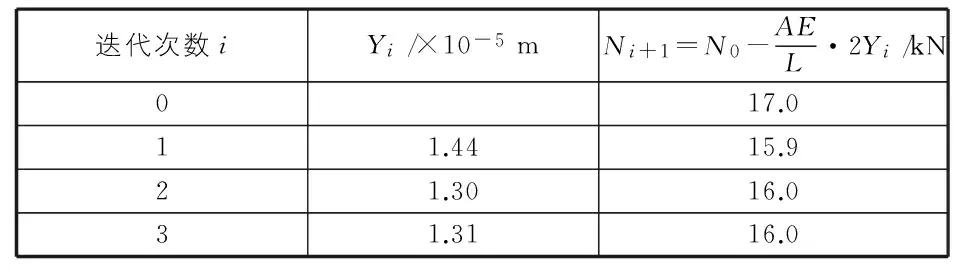
表2 第一道支撑计算结果(一)

2.2 广州地铁线网运营管理指挥中心项目基坑工程

广州地铁线网运营管理指挥中心项目基坑工程位于广东省广州市海珠区，广州地铁四号线与八号线交汇站万胜围站A出口周边地块，万胜围地铁站A出口西侧，北临新港东路，东临70m宽规划路，与大型住宅小区城市花园邻近。基坑围护结构采用φ1 000@1 150的灌注桩支护，桩长16.8m，设置两道钢支撑，现场工程如图6所示。

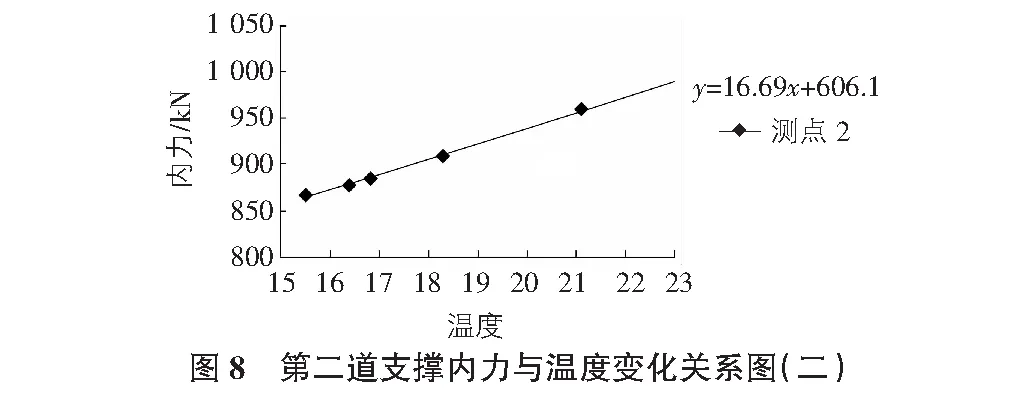
由本文建立的模型可知，基坑深度15.22m，h1=6.500m，H1=2.575m，h2=6.145m，H2=9.075m，m2=2 000kN/m4，m3=3 000kN/m4，灌注桩刚度K′=k2hnD=20MN/m，对撑分担的基坑周边长度为D=40m，支撑长度L=57.0m，支撑横截面积A=0.017 189m2，α=12×10-6，钢支撑的弹性模量E=2.06×108kN/m2，N0=α·φ·ΔT·A·E，φ=0.4，N0=17.0kN,计算结果如表3，表4所示。本工程中采用自动监测系统，在钢结构支撑中实现24h连续测量温度和钢结构的轴向内力，第一、二道支撑实测的内力与温度的变化关系如图7，图8所示。实测得在单位温度下，第一道钢支撑轴力变化为15.5kN～16.5kN，第二道钢支撑轴力变化为16.5kN～17.5kN，计算结果与实测的相近，约相差5%，所以模型建立合理。

表3 第二道支撑计算结果(二)

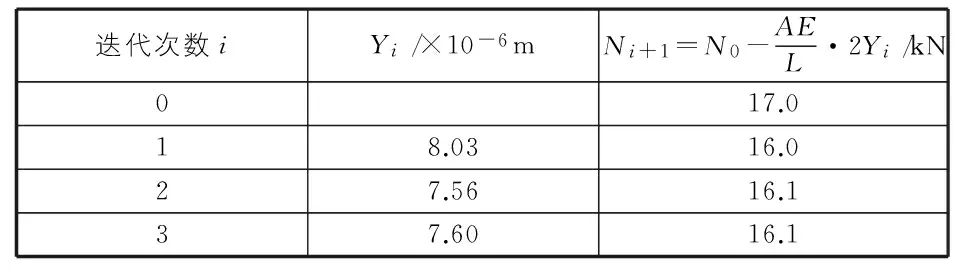
表4 第一道支撑计算结果(二)

3 影响温度内力的因素分析及调整方法

3.1 土层的性能

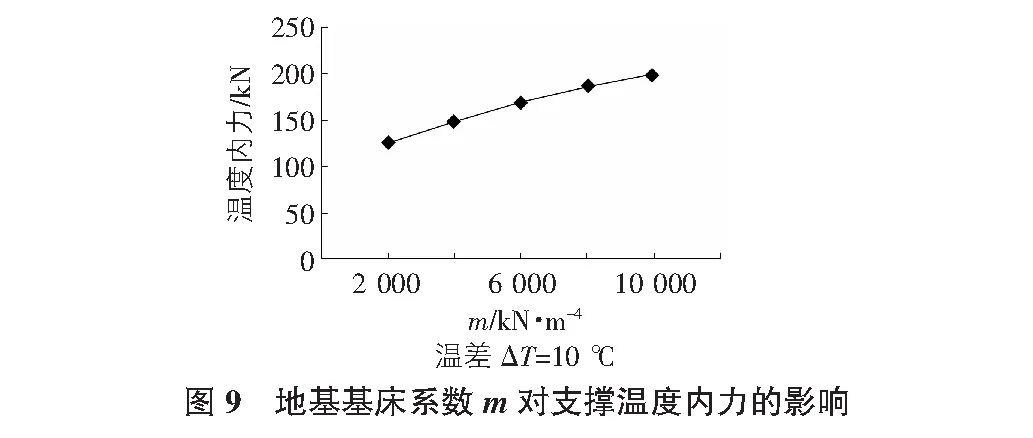
结合实际工程情况,考虑围护墙后土体的刚度随着不同土层的变化，进一步分析围护墙后土体的分布和土层的性能对支撑温度内力的影响。本文采用弹性地基梁法，将围护墙后土体看作土弹簧，通常采用m法计算水平抗力系数，因土层性能的不同，地基基床系数m随之变化，水平抗力系数以及地基土反力也随之不断变化，从而影响水平支撑的温度内力。根据本文计算模型，分别取地基基床系数m为2 000kN/m4，4 000kN/m4，6 000kN/m4，8 000kN/m4，10 000kN/m4，温差ΔT=10 ℃，计算各道支撑的温度内力变化,计算结果如图9所示。从图9可以看出,当地基基床系数m越大时，地基的土反力也越大，导致支撑的温度内力也越大。因此，对深大基坑来说，土层的性能对水平支撑的温度应力有很大影响。

3.2 围护桩的刚度

实际工程中的深大基坑往往采用连续墙和大刚度支撑围护桩体系,此时围护桩的刚度对支撑温度内力的影响不可忽略。围护桩的刚度越大，围护桩的约束作用就越强，支撑的温度内力就越大。故在支撑温度内力的计算中，应考虑围护桩的刚度对其的影响。根据本文计算模型，分别取围护墙刚度为10MN/m，15MN/m，20MN/m，25MN/m，30MN/m，35MN/m，40MN/m，温差ΔT=10 ℃，计算各道支撑的温度内力变化,计算结果如图10所示。从图10可以看到,由于墙体的约束作用,支撑的温度内力变大,并且围护墙刚度越大，约束作用越强，支撑温度应力越大。因此，对深大基坑来说，采用大刚度围护桩体系,当温度变化比较大时,水平支撑容易产生较大的温度内力,在设计和施工时不能忽略。

3.3 支撑的长度

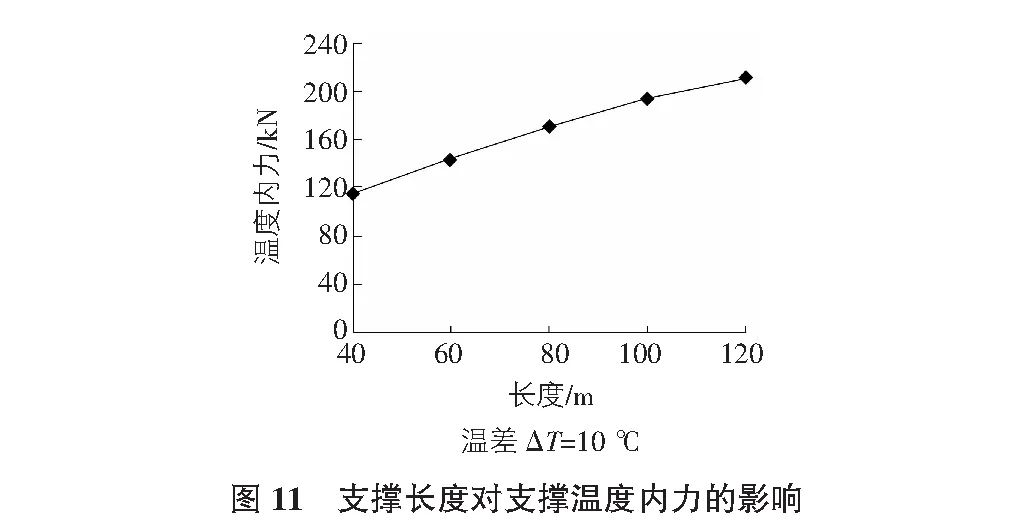
当两端为固定约束时，支撑的温度应力与支撑长度无关。但在基坑开挖系统中，由于支撑—竖向围护结构—周边土层的相互作用，土体和围护提供给支撑的约束并不是理想固定的，支撑的长度影响着支撑的绝对变形，而支撑的变形又影响着围护的变形以及土压力的分布变化，所以支撑的长度也是影响支撑温度应力的一个重要因素。通过对多个内支撑内力监测结果可看出120m长度内支撑的单位温度内力变化量达21kN以上，所以不可忽略支撑长度对支撑温度内力的影响。为了分析支撑长度对支撑温度内力的影响，将计算模型中的支撑长度L取40m，60m，80m，100m，120m,温差ΔT=10 ℃， 计算各道支撑的温度内力变化,计算结果如图11所示。从图11可以看出,对于深大基坑来说,随着支撑长度的增大，支撑内力也随之增加，因此，对深大基坑来说，土层的性能对水平支撑的温度应力有较大影响。

3.4 支撑内力的调整方法

从监测结果和计算结果可以看出，当支撑长度较大、温度的变化幅度较大时，产生的温度内力也较大。通过支撑温度应力的计算，掌握支撑轴力的变化规律并科学合理地采取措施，使“温差影响”变为“温差控制”，才能保证深基坑的安全。由此可知，现行的钢筋混凝土支撑因无法调节内力将会导致由温度变化而产生较高的内力，导致支撑破坏，为保证安全必须增大支撑的截面积或材料强度，将会增加工程造价。由于大跨度的预应力鱼腹梁钢支撑可以调节内力，可以有效消除温度内力的影响，具体的调整方法如下：尽量避免每日气温最高或最低时施加预应力；要牢牢依据气象部门天气预报、正确掌握季节以及昼夜温差的变化规律及时对支撑轴力作适当地调整。例如在暴风雨前气温已有落差时快速增加轴力而在暴风雨后气温已有升幅时快速释放轴力，内力调整的现场如图12所示。

4 结语

本文在前人研究的基础上，考虑多层地基土、多道水平支撑及竖向围护墙的相互作用，基于Winkler地基模型，考虑围护墙后的土体的刚度随着不同土层的变化，进一步分析围护墙后土体的分布和土层的性能对支撑温度内力的影响，建立了多道水平支撑下温度内力的计算方法，通过计算结果与现场实测结果的比较，验证了所建立的温度内力与变形计算方法是可靠的，并分析了影响其温度内力变化的主要因素。本文计算方法简便，并且具有一定的精度，可供深大基坑的内支撑设计时参考。

[1]JGJ120-2012,建筑基坑支护技术规程[S].

[2] 陆培毅,韩丽君,于 勇.基坑支护支撑温度应力的有限元分析[J].岩土力学,2008,29(5):1290.

[3] 郑 刚,顾晓鲁.考虑支撑—围护桩—土相互作用的基坑支护水平支撑温度应力的简化分析法[J].土木工程学报,2002,35(3):87.

[4] 吴 明,孙鸣宇,夏唐代,等.多层支撑深基坑中考虑支撑—围护桩—土相互作用的水平支撑温度应力简化计算方法[J].土木工程学报,2009,42(1):91.

Indeepbigholeexcavatedforbuildingfoundationlevelsupporttemperatureendogenicforceanddistortioncomputationalmethod★

FANJun-yu

(ShanghaiQiangjinFoundationEngineeringCo.,Ltd,Shanghai200233,China)

Take the deep big hole excavated for building foundation supports and protections structure as the object, has established the deep big hole excavated for building foundation level support temperature endogenic force and the distortion computational method. Through the computed result and the scene actual result comparison, has confirmed the temperature endogenic force and the distortion computational method which establishes is reliable, may supply the deep big hole excavated for building foundation in supports designs when to refer, thus also in the certificate deep big hole excavated for building foundation in supports the endogenic force adjustable is controls the hole excavated for building foundation distortion and the guarantee security effective method.

deep hole excavated for building foundation, multi-layered earth, Winkler model, temperature endogenic force

1009-6825(2014)18-0059-04

2014-04-13★：住房和城乡建设部2013年科学技术项目计划(项目编号：2013-K3-9)

范君宇(1979- )，男，硕士

TU463

A