基于强度折减有限元法的边坡稳定性分析

吴思雄 孙 涛

(1.福建省建筑科学研究院，福建 福州 350025； 2.中国人民解放军92304部队，海南 三亚 572011)

基于强度折减有限元法的边坡稳定性分析

吴思雄1孙 涛2

(1.福建省建筑科学研究院，福建 福州 350025； 2.中国人民解放军92304部队，海南 三亚 572011)

将大型有限元软件ABAQUS与强度有限元法相结合，采用特征点位移增量的突变及塑性区的贯通作为边坡失稳破坏准则，对边坡失稳过程进行了数值模拟与分析，通过算例分析，并与Slope软件计算得到的安全系数进行对比，验证了该方法的合理性与可行性。

边坡稳定，强度折减法，ABAQUS，安全系数，破坏过程

边坡稳定性分析是边坡工程的核心问题，也一直是岩土工程中重要的研究领域，至今已出现数十种分析方法。就目前工程应用而言，主要是极限平衡法和有限元分析法。传统的极限平衡法考虑了土体的强度特性，但未考虑土体本身的应力应变关系，无法得到边坡破坏过程中，坡内的应力与应变的空间分布，计算过程中，需要事先知道边坡滑动面的位置和形状，无法搜索出边坡的最危险滑动面以及得到相应的安全系数，从而使极限平衡法的应用受到一定限制。有限元分析边坡稳定性问题，不但可以考虑土体本身的弹塑性关系，得到各土体单元的位移、应力应变关系，还可以模拟边坡的破坏过程，得到相应的滑动面。此外，有限元分析法可以模拟复杂边界条件，求解安全系数时，不需要条分和假定土条为刚体。强度折减有限元法在目前边坡稳定分析中应用较为广泛，其将强度折减原理与有限元分析方法相结合，通过不断调整折减系数的大小，对边坡稳定性进行分析，求出边坡稳定的最小安全系数[8,9]。本文运用大型有限元分析软件ABAQUS，结合强度折减法对边坡稳定性进行了分析，并利用ABAQUS强大的后处理功能，对边坡的失稳破坏过程进行了模拟。

1 强度折减有限元法

1.1 强度折减法的基本原理

强度折减法是1975年ZIENKIEWICZ等[1]在土工弹塑性有限元数值分析一文中首次提出，他们提出了一个抗剪强度折减系数(SSRF：Shear Strength Reduction Factor)的概念，由此所确定的强度储备安全系数与Bishop在极限平衡法中所给出的稳定安全系数在概念上是一致的[2]。抗剪强度折减系数的定义为：在外荷载保持不变的情况下，边坡内土体所能提供的最大抗剪强度与外荷载在边坡内所产生的实际剪应力之比。在极限情况下，外荷载所产生的实际剪应力与抵御外荷载所发挥的最低抗剪强度即按照实际强度指标折减后所确定以及实际中得以发挥的抗剪强度相等。强度折减法的基本原理是岩土体材料的强度参数c，φ同时除以一个强度折减系数Fr，得到折减后的强度参数cr，φr，其表达式为：

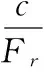
(1)

其中，c和φ均为土体所能提供的抗剪强度；cr和φr均为土体实际发挥的抗剪强度；Fr为强度折减系数。

整个计算过程中通过不断增加Fr，使用折减后的材料参数进行有限元试算，当计算不收敛或边坡达到临界破坏时的强度折减系数即为边坡稳定安全系数[3]。

1.2 屈服准则的选取

屈服准则的选取与边坡稳定安全系数的大小有着密切关系，不同的屈服准则得到的安全系数有一定的差异性。本文求解边坡稳定问题时，采用理想弹塑性模型，屈服准则采用Mohr-Coulomb破坏准则，其表达式为：

(2)

其中，I1和J2分别为应力张量第一不变量和应力偏量第二不变量；c和φ分别为土的粘聚力和内摩擦角；θ为应力罗德角。

1.3 流动法则的选取

在有限元计算中，流动法则的选取与剪胀角ψ值的选取有关。当ψ=φ时，即剪胀角等于土的内摩擦角时，为相关联流动法则；当ψ≠φ时，即剪胀角不等于内摩擦角时，为不相关联流动法则。对于同一类材料，采用相关联流动法则所得到的破坏荷载比采用不相关联流动法则所得到的破坏荷载大，但如果忽略剪胀角的影响，即ψ=0，则会得到较为保守的结果。岩土类材料不适应相关联流动法则，由此得到的应力应变关系与土的实际应力应变关系有较大偏离，但采用不相关联流动法则只能在一定程度上减少剪胀效应，且剪胀角值的选取具有很大的随意性，增大了计算土性参数与实际土性参数的差距，带来了新的计算误差[4]。综合以上考虑，本文选取相关联流动法则。

1.4 边坡失稳的判据

采用强度折减有限元法分析边坡稳定性的一个关键问题就是如何根据有限元计算结果判别边坡是否处于临界破坏状态。目前，边坡失稳破坏的判别依据主要有三种[5,6]：1)有限元数值迭代计算不收敛；2)特征点位移增量发生突变；3)潜在滑移面的塑性区贯通。利用有限元迭代计算的收敛性判别边坡的稳定性与计算方法有关，且该算法在边坡工程问题中受到一定的限制，适用性较差[7]；根据边坡内某特征点的位移与折减系数的关系曲线判别边坡的失稳状态，即当折减系数增加到某一值时，边坡内特征点的位移增量发生突变，则认为边坡处于临界破坏状态，继续增大折减系数，边坡将发生失稳破坏，但该方法中特征点的选取对安全系数的计算结果影响较大[7]；塑性应变的产生及塑性区的发展，表示着在失稳破坏过程中边坡内的土体变形中不可恢复的塑性变形，以边坡内潜在滑移面的塑性区贯通作为边坡失稳破坏的依据，有着明确的物理意义，但边坡的等效塑性变形区的贯通是边坡破坏的必要条件，而不是充分条件[5]。

综合以上考虑，边坡的失稳破坏过程既是边坡内塑性区逐步扩展贯通的过程，也是边坡内各点位移增量不断增长的过程，因此，本文结合判据2)，3)综合判定边坡的失稳状态。

2 算例分析

本文选用澳大利亚计算机应用协会(ACADS)的考题作为标准算例(参考文献)，运用强度折减法对该边坡的稳定性进行分析，利用失稳判据得到边坡的稳定安全系数，并与Slope软件计算出来的安全系数进行比较，同时，利用ABAQUS强大的后处理功能，对边坡的破坏过程进行了模拟。边坡稳定分析的有限元模型采用的是CPE4四节点平面应变单元，底部固定X，Y两个方向的位移，左右边界固定X方向的位移，模型受重力荷载作用，选择边坡坡面右上角的顶点作为特征点。有限元模型和网格划分分别见图1和图2，土体的计算参数见表1。

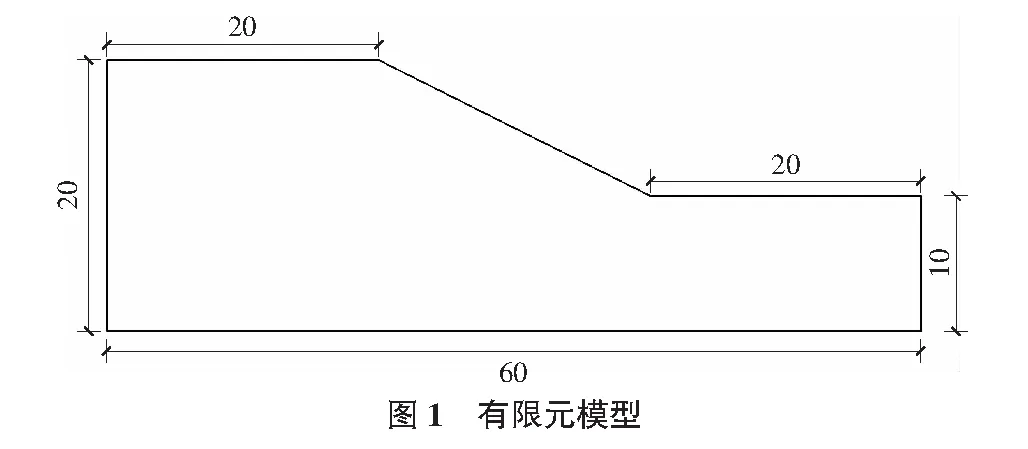
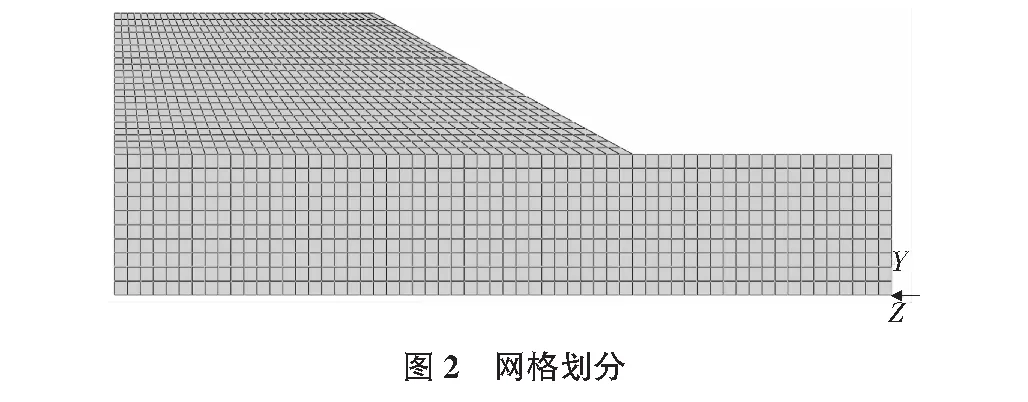
表1 土性参数

密度ρ/kg·m-3弹性模量E/MPa粘聚力c/kPa内摩擦角φ/(°)泊松比μ20001032100.25

计算结果及分析。

1)安全系数。利用ABAQUS后处理中提供的Combine函数，绘制边坡坡面右上角的顶点的水平位移U1随强度折减系数FV1的关系曲线(见图3)，以该特征点水平位移增量发生突变，即FV1—U1关系曲线的拐点作为边坡失稳破坏的评价标准，由图可知，边坡的安全系数为1.71。

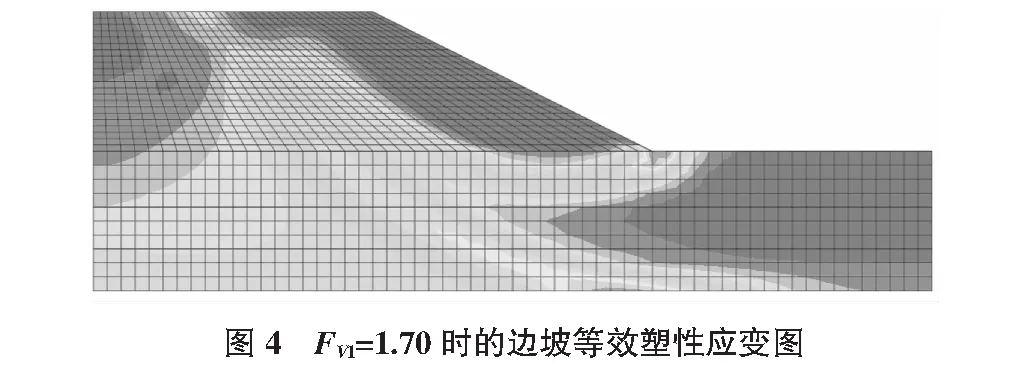
同时，本文给出了折减系数为1.70时的边坡等效塑性应变图(见图4)，从图上可以看出，当折减系数达到1.70时边坡坡顶已经出现塑性区，且与坡体的塑性区开始贯通，此时，可认为边坡已经处于临界破坏状态，若折减系数继续增大，则边坡坡体内的塑性区将继续扩展，最后形成连续的滑动面，边坡将发生失稳破坏。综合考虑，可以确定边坡的稳定安全系数为1.71。

对于此模型，采用Slope软件中的简化Bishop法得到的安全系数为1.690，ACADS对该模型给出的安全系数的参考值为1.65～1.70(参考文献)。本文得出的结果与ACADS给出的参考值比较接近，与Bishop法得到结果也仅仅相差1.18%，这在一定程度上也验证了本方法的合理性与可行性。

2)边坡失稳破坏过程。本文结合边坡内塑性区的发展情况及边坡失稳破坏时的位移等值线云图，模拟并探讨了边坡失稳破坏的发展过程。图5给出了不同时刻边坡的等效塑性应变图。

从图上可以看出，边坡的失稳破坏大致分为三个阶段：a.初始破坏阶段。荷载开始施加时，边坡坡脚处和潜在滑动面周围的土体单元首先出现塑性变形，随着荷载的继续增加，土体的变形也不断增长，滑动面开始形成，边坡的位移也开始持续增长，见图5a)，图5b)；b.稳定变形增长阶段。随荷载的持续增加，边坡内的土体单元的变形和位移继续增长，同时边坡内的塑性区也随变形的增加而不断扩展，见图5c)；c.失稳破坏阶段。随着时间的增加，坡内的塑性区贯通并延伸至坡顶，坡内连续滑动带形成，若荷载继续增加，边坡将发生失稳破坏，见图5d)。

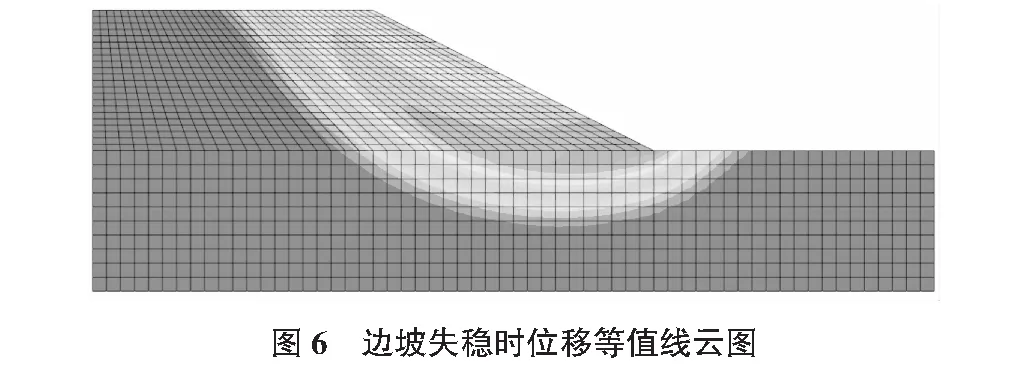
图6给出了边坡失稳破坏时的位移等值线云图。从图上可以看出，边坡破坏时塑性区已贯通至坡顶，这与等效塑性应变图得出的结果是一致的。从图上可以清晰的判断出滑动面的位置，这与Slope软件得出的结果大致是一致的。

3 结语

本文将ABAQUS软件与强度折减法相结合，针对一算例，对边坡的失稳过程进行了模拟和分析，对本文方法得出的边坡稳定安全系数与采用Slope软件Bishop法得出的安全系数进行了对比分析，表明采用本文判别依据得出的边坡稳定安全系数的可靠性，同时也验证了采用特征点位移增量的突变结合潜在滑移面塑性区的贯通作为边坡失稳破坏判据的合理性与可行性。此外，本文利用ABAQUS软件的动态图像显示技术，依据边坡内等效塑性区发展情况和失稳破坏时坡内位移等值线云图分布情况，模拟了边坡失稳破坏的过程，初步探讨了边坡失稳破坏的机制和阶段。

边坡的稳定分析是一个持久而又常新的问题，本文的分析也仅仅局限于二维静力边坡，对于三维状态和动力状态下边坡的稳定分析，还有待研究。

[1] ZIENKIEWICS O C,HUMPHESON C,LEWIS R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Geotechnique,1975,25(4):671-689.

[2] Bishop A W.The use of the slip circle in the stability analysis of slopes[J].Geotechnique,2000(3)：19-55.

[3] 费 康，张建伟.ABAQUS在岩土工程中的应用[M].北京：中国水利水电出版社，2010.

[4] 张鲁豫，郑颖人，赵尚毅，等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报，2003(1):21-27.

[5] 栾茂田，武亚军，年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报，2003,23(3):1-8.

[6] 万少石，年廷凯，蒋景彩，等.边坡稳定强度折减有限元分析中的若干问题讨论[J].岩土力学，2010,31(7):2283-2288.

[7] 宋二祥.土工结构安全系数的有限元计算[J].岩土工程学报，1997,19(2):1-7.

[8] 李春忠，陈国兴，樊有维.基于ABAQUS的强度折减有限元法边坡稳定分析[J].防灾减灾工程学报，2006,26(2):207-212.

[9] 周容方，雷学文，孟庆山，等.基于ABAQUS的土质边坡渐进性破坏数值模拟[J].土工基础，2012,26(4):56-59.

Analysis on slope stability of strength reduction finite element method

WU Si-xiong1SUN Tao2

(1.Fujian Academy of Building Science, Fuzhou 350025, China; 2.China People’s Liberation Army 92304, Sanya 572011, China)

Combining large-scale finite software ABAQUS with strength reduction finite- element method, the paper takes displacing point increasing amount and plastic region connection as slope instability damage rules, carries out numerical simulation and analysis of slope instability process, through analysis example, compares its safety coefficient it with that of Slope software calculation method, and finally proves its rationality and feasibility.

slope stability, strength reduction method, ABAQUS, safety coefficient, destruction process

1009-6825(2014)31-0113-03

2014-08-22

吴思雄(1987- )，男，助理工程师； 孙 涛(1987- )，男，助理工程师

TU413.62

A