未确知测度理论在采空区危险性评价中的应用
2014-08-08吴和平
吴和平 周 旭
(鑫达金银开发中心,北京 100038)
未确知测度理论在采空区危险性评价中的应用
吴和平 周 旭
(鑫达金银开发中心,北京 100038)
采空区灾害是矿山频繁高发的灾害之一。将未确知测度理论用于评价采空区的危险性,考虑到空区稳定性影响因素数值的易取性和显著性,经综合分析,选取空区岩体结构、地质构造、围岩抗压强度、水文因素、采空区布置形状、矿体倾角、高跨比、采空区体积、埋深、最大暴露面积、暴露时间、采动扰动情况、相邻空区情况等13项因素作为空区危险性的判别指标。根据空区危险性等级和评价指标的分级标准,结合采空区失稳机理和相关研究成果,建立评价指标的单指标测度函数,采用信息熵理论计算指标权重和综合测度,依照置信度识别准则进行等级判定。对某金属矿12组空区危险性进行评判。结果表明,该法的判别结论与采用模糊综合评判法和物元分析方法得出的结果完全相符,这充分说明该方法是可靠实用的,可以在工程实践中推广应用。
采空区危险性 未确知测度 采空区 稳定性 熵权
近年来,国内外学者对采空区危险性评价开展了大量的研究,研究方法主要为数值模拟方法和数理统计方法2类。李俊平等[1]率先将ANSYS用于采空区危险性评价并取得了良好的效果。刘科伟等[2]根据三道庄矿CALS空区探测结果,利用Surapc-FLAC3D耦合技术对空区危险性进行了分析,结果令人非常满意;杜坤等[3]采用Midas/GTS对老鸦巢矿采空区进行建模并模拟分析,分析结果与采用物元分析法的评价结果基本吻合;寇向宇等[4]和倪彬等[5]分别基于CMS-Dimine-FLAC3D耦合技术和Phase2软件对采空区稳定性成功进行了模拟。此外,还有一些数理统计方法如模糊数学、灰色理论、BP神经网络、遗传算法等[6-9]相继被用于评价采空区的危险性。由于影响采空区危险性的因素很多,既有确定性的,又有未知的,为了更加合理、可靠地评价采空区的危险性,必须把这些未知的因素充分考虑在内,而未确知测度理论在这方面则优势明显。鉴于此,本研究将这一理论用于评价采空区危险性的研究中。
1 未确知测度理论
未确知测度理论是由王光远于1990年创立[10],在此基础上,刘开第和赵国彦等[11-12]对其进行了发展和完善。目前,它被广泛应用于各个领域的模式识别、项目决策、分类评价和聚类预测等问题中并且应用效果非常理想。
一个分类评价问题可以表示为:若Q1,Q2,…,Qn为n个待评价的对象,那么评价对象空间可记为

对于评价对象空间中的任一子集Qi(i=1,2,…,n)均有m个影响其大小的因素即评价指标,记为

那么,Qi可表示为m维向量

其中,xij表示研究对象Qi关于评价指标Xj(j=1,2,…,m)的测量值或量化值。对于每个指标值xij,假设有z个评价等级{C1,C2,…,Cz},若将评价类别空间记作C,那么
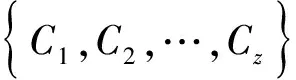
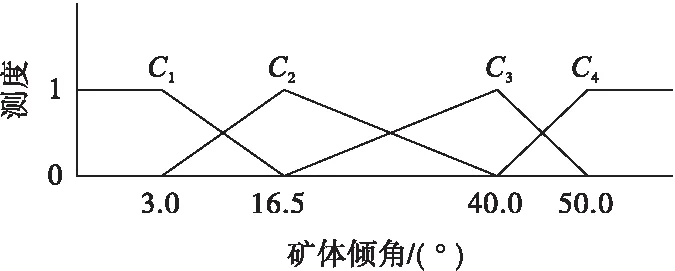
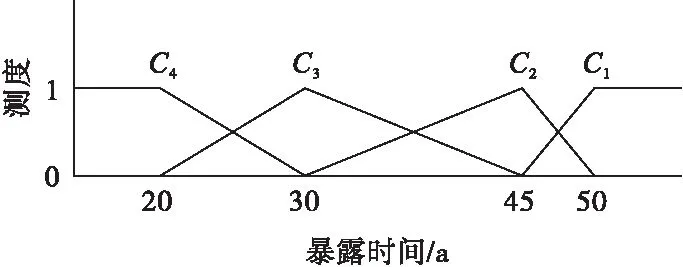
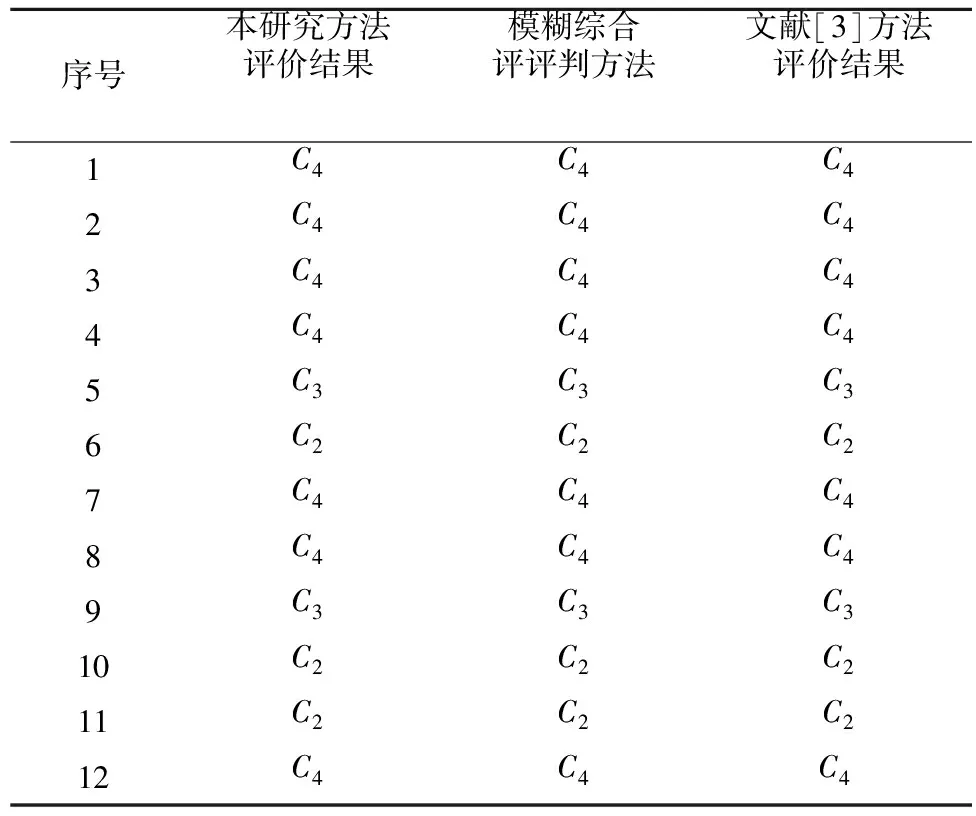
设Ck为(k=1,2,…,z)评价对象所属的第k级评价等级且第k级比第k+1级危险等级“高”或“低”,记为Ck>Ck+1或Ck 1.1 单指标测度 记μijk=μ(xij∨Ck;i=1,2,…,n;j=1,2,…,m;k=1,2,…,z)表示评价指标值xij属于第k个评价等级Ck的程度或概率,同时要满足 0≤μ(xij∈Ck)≤1, (1) μ(xij∈C)=1, (2) (3) 若μ同时满足式(1)~式(3),则μ称为测度或未确知测度,式(2)和式(3)分别代表未确知测度的“归一性”和“可加性”,那么评价对象的单指标测度矩阵(μijk)m×z可记为 (4) 1.2 指标权重和多指标综合测度向量的确定 a=(a1,a2,…,am). 过去人们普遍采用AHP法、专家打分法、Delphi法等方法确定指标权重,但这些方法在应用上受人为主观性的影响,误差较大。对此,笔者采用信息熵理论计算指标权重,系统无序的程度可用熵权来反映,用熵c(j)表示对象Qi评价指标的权重aj为 (5) (6) (7) 式(6)中,规定0lg0=0,记μik=μ(xi∨Ck;i=1,2,…,n;k=1,2,…,z)表示样本xi属于第k个分类Ck的隶属度,则 (8) μi=(μi1,μi2,…,μiz) 称为评价对象Qi的多指标综合测度向量。 1.3 确定评价对象所属等级 若评价类别空间 满足上述有序分割集的有序性条件,记置信度为ε,ε定义域为0.5≤ε≤1,评价对象Qi的多指标综合测度向量μi若满足 (9) 那么,评价对象Qi的分类等级则为k0等级,根据经验,ε一般取0.6。 影响采空区危险性的因素既有自然因素,又有人为因素,这些因素相互制约,且又存在复杂的非线性关系。评价指标的选取应遵循影响显著、代表性强、易于获取、易于量化并能以少量评价指标并能反映全面信息等原则。结合前人研究成果[4,13-16],综合考虑各项指标的重要性及数据的有效性,选取岩体结构、地质构造、围岩抗压强度、水文因素、采空区布置形状、矿体倾角、高跨比、采空区体积、埋深、最大暴露面积、暴露时间、采动扰动情况、相邻空区情况等13项因素作为判别指标,分别用X1、X2、X3、X4、X5、X6、X7、X8、X9、X10、X11、X12、X13表示。同时,将空区危险性定性指标分为4类:危险性极高、危险性较高、危险性一般和危险性较低,分别用C1、C2、C3、C4表示,相应的赋值分别为1、2、3、4。判别指标的定性和定量分级标准见表1、表2。 表1 采空区危险性评价的定性指标分级及赋值 表2 采空区危险性评价的定量分级标准 以某地下金属矿山为实例,调查分析该矿山得出12组采空区数据,继而运用本文方法对采空区危险性进行分析,采空区相关指标数据见表3。 表3 采空区危险性评价指标统计 3.1 构建单指标测度函数 根据单指标测度函数的定义,基于上述指标值和分级标准,分别构建各评价指标的单指标测度函数。其中,围岩抗压强度、矿体倾角、高跨比、采空区体积、埋深、暴露面积、暴露时间等7项定量指标的单指标测度函数如图1~图7。岩体结构、地质构造、水文因素、空区布置、采动扰动、邻近空区等6项定性指标的单指标测度函数如图8。 图1 围岩单轴抗压强度单指标测度函数 图2 矿体倾角单指标测度函数 图3 高跨比单指标测度函数 图4 采空区体积单指标测度函数 图5 埋深单指标测度函数 图6 空区暴露面积单指标测度函数 图7 空区暴露时间单指标测度函数 3.2 计算指标权重 图8 定性指标单指标测度函数 根据式(5)~式(7),基于样本集计算评价指权重,权重向量为 a=(a1,a2,…,a13)= (0.080 3,0.079 2,0.073 3,0.082 6,0.080 6, 0.083 8,0.076 4,0.066 2,0.068 2,0.069 5, 0.080 6,0.080 3,0.079 0). 3.3 评判结果及分析 以第1组采空区(样本1)数据为例,根据判别指标数值或量化值,分别代入图1~图8计算13个判别指标的单指标测度,由此得出单指标测度矩阵为 结合权重向量,将单指标测度矩阵代入式(8)求出样本1的多指标综合测度向量为 μ1=(μ11,μ12,μ13,μ14)= (0.149 7,0.021 5,0.059 1,0.769 7). 根据置信度识别准则,取ε为0.6,由式(9)可得,k0为4,即第1个采空区危险性等级为C4。同理,可依次计算出其余11组采空区的危险性等级,计算结果如表4。 由表4可知,1、2、3、4、7、8、12号采空区危险性较低,对矿山安全生产不构成威胁;5、9号采空区危险性一般,在生产中应加强监测和防范;6、10、11号3个采空区危险性较大,应根据矿山情况及时采取相应的措施处理采空区,如充填空区、崩落围岩、支撑空区、封闭或隔离空区等。同时,为了检验本文方法评价采空区危险性的可靠度,研究分别采用模糊综合评判方法和文献[3]中的物元分析方法对上述12组采空区危险性进行分析,见表4。结果表明,采用未确知测度理论得出的评价结果和采用模糊综合评判法、物元分析法得出的结论完全相符。由此可见,将未确知测度理论用于采空区危险性评价中是科学可行的。 表4 采空区危险性的未确知测度评价结果 (1)采空区灾害是目前矿山频繁高发的灾害之一,对隐伏采空区及时进行探测、评价和处理是防治采空区灾害的重要举措。对采空区的危险性进行科学合理的评价是防治空区灾害的重要环节和关键,它是决定采空区处理措施的参考依据和保证矿山安全生产的前提。一直以来,开展采空区稳定性评价都是采矿领域内的重要研究课题。 (2)通过引入信息熵理论计算因子权重对未确知测度理论进行优化,将优化后的理论用于评价采空区的危险性,为空区危险性的评判提供了一个行之有效的新方法。 (3)结合采空区失稳机理和相关研究成果,在考虑到空区稳定性影响因素数值易取性和显著性的基础上,经综合分析,选取空区岩体结构、地质构造、围岩抗压强度、水文因素、采空区布置形状、矿体倾角、高跨比、采空区体积、埋深、最大暴露面积、暴露时间、采动扰动情况、相邻空区情况等13项因素作为空区危险性的判别指标,基本反映了空区稳定性的综合状况。 (4)未确知测度理论在某矿山12组空区危险性评判中的应用结果表明,采用未确知测度方法能够准确地识别空区的危险性,由此可因地制宜的根据空区危险性程度采取相应的采空区处理方案。 (5)需要指出的是,由于采空区危险性受很多因素的影响,为了让所得的结论更加全面、科学,在今后的研究工作中,应全面考虑影响采空区危险性的影响因素,不断增加采空区危险性评价的判别指标,如围岩弹性模量、结构面、矿柱布置及采取的何种防护措施等,从而进一步提高未确知测度理论的可靠度和增强其在工程实践中的适用性。 [1] 李俊平,卢忠瑜.ANSYS在采空区稳定性安全评价中的应用[J].中国钼业,2006,30(5):13-17. Li Junping,Lu Zhongyu.Application of ANSYS in safety assessment of abandoned stope stability[J].China Molybdenum Industry,2006,30(5):13-17. [2] 刘科伟,李夕兵,宫凤强,等.基于CALS及Surpac-FLAC3D耦合技术的复杂空区稳定性分析[J].岩石力学与工程学报,2008,27(9):1924-1931. Liu Kewei,Li Xibing,Gong Fengqiang,et al.Stability analysis of complicated cavity based on CALS and coupled Surpac- FLAC3Dtechnology[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(9):1924-1931. [3] 杜 坤,李夕兵,刘科伟,等.采空区危险性评价的综合方法及工程应用[J].中南大学学报:自然科学版,2011,42(9):2802-2811. Du Kun,Li Xibing,Liu Kewei,et al.Comprehensive evaluation of underground goaf risk and engineering application[J].Journal of Central South University:Science and Technology,2011,42(9):2802-2811. [4] 寇向宇,贾明涛,王李管,等.基于CMS及Dimine-FLAC3D耦合技术的采空区稳定性分析与评价[J].矿业工程研究,2010,25(1):31-35. Kou Xiangyu,Jia Mingtao,Wang Liguan,et al.Evaluation and analysis of stability of mined-out area based on the CMS and DIMINE-FLAC3Dcoupling technique[J].Mineral Engineering Research,2010,25(1):31-35. [5] 倪 彬,张 伟,刘晓明.基于Phase2的复杂采空区稳定性分析与评价[J].矿冶工程,2013,33(3):13-16. Ni Bin,Zhang Wei,Liu Xiaoming.Stability analysis and evaluation for complex cavities based on Phase2[J].Mining and Metallurgical Engineering,2013,33(3):13-16. [6] 朱为民,李 想,陈国梁,等.基于多因素模糊综合评价的某铁矿采空区危险度评定[J].有色金属科学与工程,2011,2(4):71-75. Zhu Weimin,Li Xiang,Chen Guoliang,et al.Risk assessment on an iron goaf based on multi-factor fuzzy comprehensive evaluation[J].Nonferrous Metals Science and Engineering,2011,2(4):71-75. [7] 程爱宝,王新民,刘洪强.灰色层次分析法在地下采空区稳定性评价中的应用[J].金属矿山,2011(2):17-21. Cheng Aibao,Wang Xinmin,Liu Hongqiang.Application of gray hierarchy analysis in the stability evaluation of underground mined-out areas[J].Metal Mine,2011(2):17-21. [8] 唐胜利,唐 皓,郭 辉.基于BP神经网络的空洞型采空区稳定性评价研究[J].西安科技大学学报,2012,32(2):234-238. Tang Shengli,Tang Hao,Guo Hui.Stability evaluation of empty mine goaf based on BP neural network[J].Journal of Xi'an University of Science and Technology,2012,32(2):234-238. [9] 汪 伟,罗周全,王益伟,等.金属矿山采空区危险性辨识的遗传BP模型研究[J].中国安全科学学报,2013,23(2):39-44. Wang Wei,Luo Zhouquan,Wang Yiwei,et al.Study on genetic BP model for identifying metal mine goaf danger[J].China Safety Science Journal,2013,23(2):39-44. [10] 王光远.未确知信息及其数学处理[J].哈尔滨建筑工程学院学报,1990,23(4):52-58. Wang Guangyuan.Uncertainty information and its mathematical treatment[J].Journal of Harbin Architecture and Engineering Institute,1990,23(4):52-58. [11] 刘开第,庞彦军,孙光勇,等.城市环境的未确知测度评价[J].系统工程理论与实践,1999,19(12):52-58. Liu Kaidi,Pang Yanjun,Sun Guangyong,et al.The uncertainty measurement evaluation on a city's environmental quality[J].Systems Engineering Theory and Practice,1999,19(12):52-58. [12] 赵国彦,吴 浩.未确知聚类方法及其在松动圈厚度预测中的应用[J].科技导报,2013,31(2):50-55. Zhao Guoyan,Wu Hao.Application of unascertained clustering method for predicting the thickness of excavation damaged zone[J].Science & Technology Review,2013,31(2):50-55. [13] 唐 硕,罗周全,徐 海.基于模糊物元的采空区稳定性评价研究[J].中国安全科学学报,2012,22(7):24-30. Tang Shuo,Luo Zhouquan,Xu Hai.Evaluation of stability of goaf based on fuzzy matter- element theory[J].China Safety Science Journal,2012,22(7):24-30. [14] 冯 岩,王新民,程爱宝,等.采空区危险性评价方法优化[J].中南大学学报:自然科学版,2013,44(7):2881-2888. Feng Yan,Wang Xinmin,Cheng Aibao,et al.Method optimization of underground goaf risk evaluation[J].Journal of Central South University:Science and Technology,2013,44(7):2881-2888. [15] 贾 楠,罗周全,谢承煜,等.基于改进FAHP-复合模糊物元的地下金属矿山采空区危险性辨析[J].安全与环境学报,2013,13(3):243-247. Jia Nan,Luo Zhouquan,Xie Chengyu,et al.Risk discrimination in the goaf area in under-ground metal mine based on the improved FAHP-compound fuzzy matter element[J].Journal of Safety and Environment,2013,13(3):243-247. [16] 程爱平,高永涛,季毛伟,等.基于未确知测度理论的煤矿底板突水量预测[J].金属矿山,2014(8):157-161. Cheng Aiping,Gao Yongtao,Ji Maowei,et al.Forecast of water inrush from coal floor based on unascertained measure theory[J].Metal Mine,2014(8):157-161. (责任编辑 石海林) ApplicationofUncertaintyMeasurementTheoryinUndergroundGoafRiskEvaluation Wu Heping Zhou Xu (XindaGold&SilverDevelopmentCenter,Beijing100038,China) Goaf disaster is one of frequently-occurred mining disasters.The uncertainty measurement theory is used to evaluate the risk of goaf.Considering that the factor value for affecting the stability of the goaf are easily grasped and of significance,13 factors of goaf risks are regarded as the discriminant index by comprehensive analysis,including rock structure,geological structure,intensity of surrounding rocks,hydrological condition,goaf shape,ore-body dip,high-span ratio,goaf volume,burial depth,maximum exposure area,exposure time,mining disturbances,and the condition of the neighboring goaf.The measurement function of each evaluation index is established based on the hazard degree of underground goaf and evaluation indexes' grading standards,and combining with the mechanism of underground goaf instability and some relevant research results as well.Then,the index weights and the comprehensive measurement of multiple indicators are calculated by using the information entropy theory.The hazard degree of underground goaf can be judged by credible recognition rule.This method is used to make evaluation on hazard of 12 underground goafs in a certain metal mine.The results show that the discrimination conclusion by this method is similar to the conclusion by the fuzzy comprehensive evaluation method and the matter-element analysis method,proving that the method is reliable and practical and can be applied and promoted to the actual engineering. Goaf hazard,Unascertained measurement,Underground goaf,Stability,Entropy weight 2014-09-27 吴和平(1982—),男,工程师。 TD853.391 A 1001-1250(2014)-12-175-06



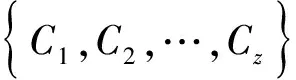
2 采空区危险性评价指标体系


3 工程实例







4 结 论
