尾矿坝风险评估中指标相关性权重的确定
2014-08-08史冬梅杨风暴王肖霞
史冬梅 杨风暴 王肖霞
(中北大学信息与通信工程学院,山西 太原 030051)
尾矿坝风险评估中指标相关性权重的确定
史冬梅 杨风暴 王肖霞
(中北大学信息与通信工程学院,山西 太原 030051)
针对现有尾矿坝风险评估方法未考虑监测指标间的相关性造成的评估过程中计算重复的问题,考虑监测指标间的相关性并将其转化为权重,使相关性的指标中占主导地位的指标权具有较小的权值,反之亦然,从而降低重复计算问题。采用综合赋权法确定权重的方法为:根据监测指标间相互影响程度不同的特点,建立影响矩阵,由于该矩阵所需专家信息具有模糊性,故采用梯形模糊数描述专家信息,计算主观权重;根据各指标监测数据具有随机、模糊等不确定性的特点,利用可能性分布对其进行表征,进而采用相关系数赋权法计算得到各指标客观权重;通过均值法综合主、客观权重。实例表明,考虑了监测指标相关性的权重确定法能减少风险评估中指标的重复计算,综合主客观权重,为尾矿坝各指标赋权提供了理论依据。
尾矿坝 风险评估 相关性 影响矩阵 可能性相关系数赋权法
尾矿坝的风险评估是目前尾矿研究方面的重点,现有风险评估模型使用的前提条件是指标间应具有独立性,是非相关的[1],即指标之间没有相互影响的关系,一个指标的变化不会导致另一个指标的变化。然而实际上,指标独立是难以实现的,如库水位升高将会导致干滩长度变短以及浸润线的升高、浸润线升高导致坝体不稳定,坝体位移量增大等[2-3]。由于指标相关性大,会带来评估过程中重复计算的问题。因此,需要尽可能地降低指标相关性对风险评估结果的影响。2个指标相关性越大,则一个指标可以被另一个指标解释得越多,在指标体系中作用也越小,即指标的权重越小。因此,本研究通过考虑监测指标相关性的权值确定方法解决评估过程中的重复计算问题。
目前尾矿坝风险评估中权重的确定方法主要有主观赋权法中的层次分析法[4]、Delphi法[5]等、客观赋权法中的离差最大化法[6]、熵权法[7]等,以及主客观结合的综合赋权法[8]。主观赋权法主观随意性大,客观赋权法所得结果可能与事实相悖,综合赋权法能够克服这二者的缺点,因此得到了广泛的应用。但是,这些权重确定方法既没有考虑指标相关性的影响,也没有考虑监测信息的随机、模糊等不确定性对权重结果的影响。
因此,利用能够考虑专家信息模糊性以及指标间相互影响程度不同的梯形模糊数影响矩阵来计算主观权重;在对尾矿坝各指标监测信息分析的基础上,利用可以表征多种不确定性的可能性分布描述各指标信息,进而利用相关系数赋权法[9]计算客观权重;综合主客观权重,得到考虑相关性的监测指标权重,为尾矿坝风险评估的进一步研究提供参考信息。
1 监测指标相关性权重确定方法
1.1 主观权重的确定
确定主观权重最常用的方法为层次分析法,该方法构建的判断矩阵是用来衡量指标重要性程度的,但是并没有考虑指标间相关性的影响。为解决这个问题,本研究构建了指标间的影响矩阵[10],并且考虑到专家信息的模糊性,引入梯形模糊数表征专家信息,使得构建的影响矩阵更合理,更准确。利用该矩阵计算尾矿坝各监测指标主观权重的具体过程如下。
1.1.1 构建影响矩阵
尾矿坝4个监测指标:库水位(u1)、浸润线(u2)、坝体位移(u3)、干滩长度(u4)的影响矩阵为
其中,aij表示指标ui对指标uj的影响程度。值得注意的是,aij不是指标的相关度。因此,一般情况下,aij≠aji,这也是不同于层次分析法的地方。该矩阵能够考虑到2个指标相互影响程度的不同。
上述矩阵请尾矿坝相关专家给出,通常采用表1所示标度对指标间影响程度定量衡量。但是专家打分本质是一个模糊过程,采用确定数值会对分析结果的精确性产生影响。因此,以表1所示标度法为基础,利用梯形模糊数表征专家信息。

表1 标度法及其含义
设专家给出的指标ui对uj影响程度的梯形模糊数为
aij=(lij,mij,nij,sij),
lij≤mij≤nij≤sij,
其隶属函数μaij(x)为
(1)
该梯形模糊数的期望值
E(aij)=bEL(aij)+(1-b)EU(aij),
(2)
其中,

为梯形模糊数的左期望值;
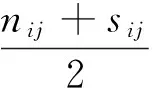
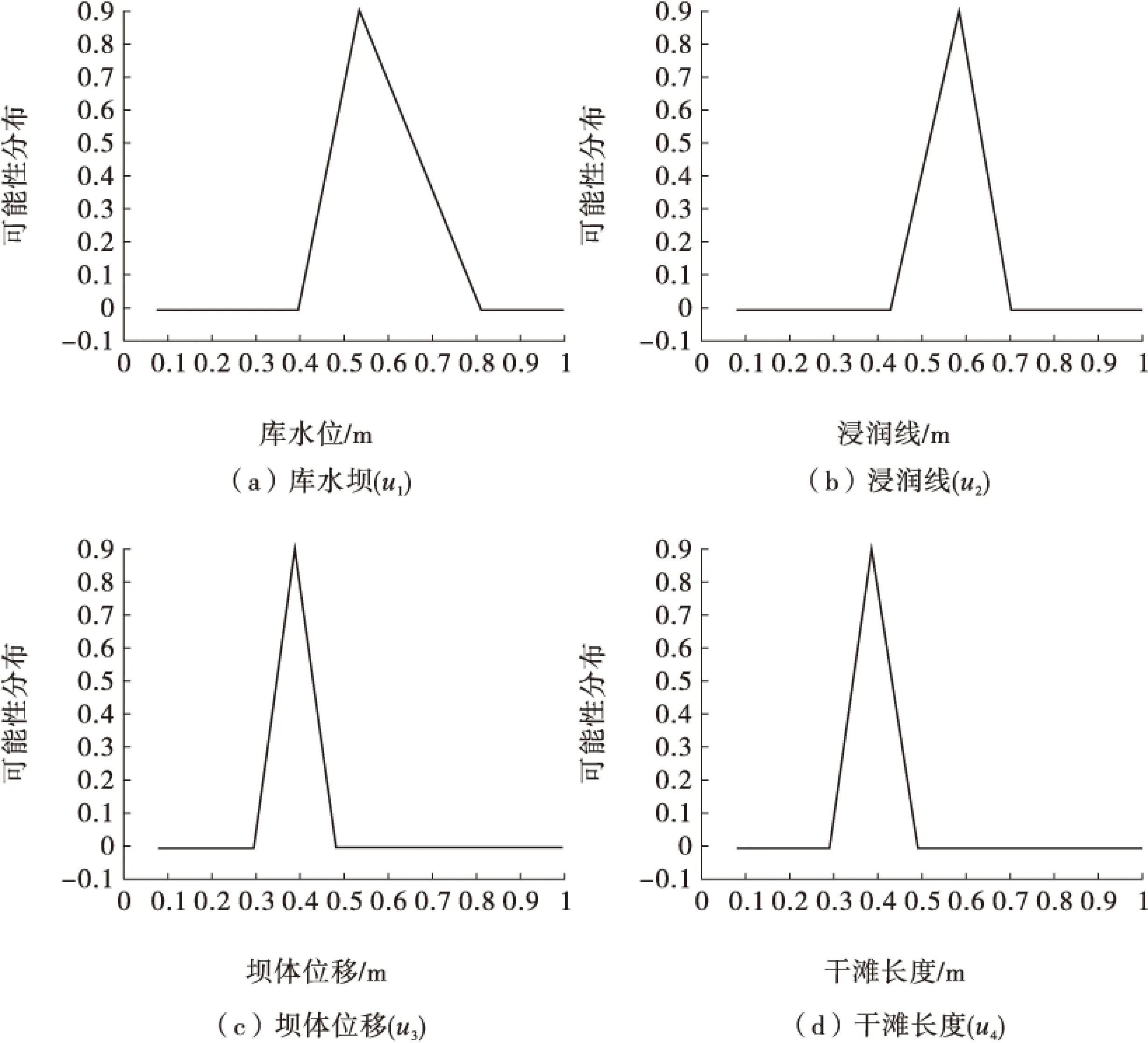
为梯形模糊数的右期望值;b为乐观系数,表明专家对所给结果的态度。如果0≤b≤0.5表明专家持偏向悲观的态度;如果0.5 1.1.2 确定指标权重 基于上述所得影响矩阵,计算尾矿坝各监测指标主观权重过程如下。 (1)计算指标ui的模糊影响值 (2)计算ui的期望值E(ui),通常取b=0.5。 (4) 1.2 客观权重的确定 由于尾矿坝坝体结构的复杂性和动态性,传感器本身监测精度与范围的局限性,自然环境影响的强干扰性等,使得尾矿坝的监测信息具有模糊、随机、不完全等不确定性,通常的相关性权重计算方法并没有考虑这些不确定性。由于可能性分布能够处理多种不确定性,故利用可能性分布表征监测信息,进而利用相关系数赋权法确定客观权重。具体过程如下。 (1)利用样本监测数据的可能性分布构造法,将尾矿坝各指标监测信息转化为三角可能性分布。 (5) 其中,π(x)为指标uj的可能性分布,m为监测数据x的均值,m1和m2分别为以均值为界限的2组监测数据的均值。 (2)计算指标间的相关系数 (6) 由此可构建出各监测指标的相关系数矩阵 (7) 其中,rij(i,j=1,2,…n)为ui与uj的相关系数,rij=1表示本身相关程度最大。该矩阵为一个对称矩阵。 (3)计算指标uj与其他指标相关程度的均值 (8) (4)如果一个指标与另一指标相关性越大,则其在指标体系中所占比重越小,即权重越小。此处认为相关性与权重有如下倒数关系 qj=1/δj, (9) (5)计算指标uj的客观权重(归一化处理) (10) 计算出尾矿坝各监测指标的客观权重W″ W″=(W″u1,W″u2,W″u3,W″u4,W″u5). 1.3 综合赋权法 将基于影响矩阵获得的主观权重与可能性相关系数赋权法所得的客观权重利用式(10)融合计算,得到权重集合 W=(Wu1,Wu2,Wu3,Wu4,Wu5) 即为尾矿坝各监测指标的权重。考虑专家经验,同时也考虑客观因素,能够比较全面地反映监测指标的相对重要程度的综合权重为 W=βW′+(1-β)W″, (11) 其中,β为主客观权重的比例因子,反映人们对权重结果偏主观一些还是客观一些,0<β≤1。通常认为主客观结果占同等重要的地位,故取β=1/2。 以山西省某尾矿坝为例来说明库水位、浸润线、坝体位移、干滩长度4个指标的权重确定过程。 专家给出的尾矿坝信息影响矩阵为 根据该影响矩阵计算出主观权重为 W″u1=0.316 0,W″u2=0.255 8, W″u3=0.189 2,W″u4=0.239 1. 将尾矿坝各指标监测信息利用式(5)转化为对应的可能性分布,如图1所示。 根据上述可能性分布,利用式(6)计算指标间相关系数,得相关系数为 通过计算可得客观权重: W″u1=0.280 0,W″u2=0.248 0, W″u3=0.235 4,W″u4=0.236 4. 熵权法所得客观权重: wu1=0.251 2,wu2=0.251 2, wu3=0.247 7,wu4=0.250 0. 将2组客观权重对比分析可知,可能性相关系数赋权法相比于熵权法,能够将具有相关性的指标通过权重的方式进行调整,将在相关性中占主导地位的指标赋予较小权值,从而更加合理地确定指标权重,消除由于指标重复对风险评估结果的影响。 利用式(10),得到综合主客观权重: Wu1=0.298 1,Wu2=0.251 9, Wu3=0.212 3,Wu4=0.237 8. 图1 各指标监测信息可能性分布 本研究在确定尾矿坝监测指标权重时,考虑了指标间的相关性问题,所采用的方法为主客观结合的综合赋权法。主观赋权法通过梯形模糊数影响矩阵得到,不仅考虑了每对监测指标的相互影响程度的不同,还用梯形模糊数表征了专家信息的模糊性;客观赋权法利用可能性相关系数赋权法计算得到,该方法利用可能性分布表征监测信息多种不确定性,同时将指标间的相关性以定量的方式衡量,转化为权重,从而解决风险评估中指标重复计算的问题。 [1] Hai Yanju,Gui Qinggao,Qiu Xiangli,et al.Analysis of safety and risk factors about the tailings dam in the metal mines[J].Advanced Materials Research,2012,594/597:299-302. [2] 戴 绘,秦卫星,张岳安.强降雨作用下山谷型尾矿坝浸润线演化规律[J].金属矿山,2013(7):149-152. Dai Hui,Qin Weixing,Zhang Yuean.Evolution law of phreatic line in valley-type tailings dam under heavy rainfall[J].Metal Mine,2013(7):149-152. [3] 刘海明,曹 净,杨春和.国内外尾矿坝事故致灾因素分析[J].金属矿山,2013(2):126-129. Liu Haiming,Cao Jing,Yang Chunhe.Analysis of factors for tailings dams accidents causing disaster at home and abroad[J].Metal Mine,2013(2):126-129. [4] Yan Shanyu,Dong Yang,Pan Ke.Application of multi-level extensible method in risk assessment of tailings dams failure[J].Journal of Northeastern University,2013,34:80-83. [5] Mei Guodong,Wu Zongzhi.Study on social risk evaluation index system for tailings pond dam-break based on the vulnerability theory[J].Advanced Materials Research:Advances in Industrial and Civil Engineering,2012,594/597:2301-2308. [6] 张影秋,吴瑞明,张 扬.基于离差最大化与灰色关联分析的危险源辨识方法[J].科学技术与工程,2010,10(25):6358-6362. Zhang Yingqiu,Wu Ruiming,Zhang Yang.The method of hazard identification based on maximizing deviations and grey relational analysis[J].Science Technology and Engineering,2010,10(25):6358-6362. [7] 袁 维,白 冰,李小春,等.透镜体对尾矿坝安全性影响的参数敏感性分析[J].中南大学学报:自然科学版,2013,44(3):1174-1183. Yuan Wei,Bai Bing,Li Xiaochun,et al.Parameters sensitivity analysis of lenticles' impacting on tailings dam safety[J].Journal of Central South University:Science and Technology Edition,2013,44(3):1174-1183. [8] 王肖霞,杨风暴,史冬梅.可能性熵权在尾矿坝风险评估中的应用[J].科学技术与工程,2013,13(20):5766-5771. Wang Xiaoxia,Yang Fengbao,Shi Dongmei.Application of possibility entropy weight in security risk assessment of tailing dam[J].Science Technology and Engineering,2013,13(20):5766-5771. [9] 吕明捷,杜 云,荣 超,等.基于相关系数定权的集对分析法在湖泊富营养化评价中的应用[J].南水北调与水利科技,2011,9(1):96-98. Lu Mingjie,Du Yun,Rong Chao,et al.Set pair analysis method in lake's eutrophication assessment based on correlation weight method[J].South to North Water Transfers and Water Science & Technology,2011,9(1):96-98. (责任编辑 徐志宏) Determining of Correlation Weights of Index in the Tailing Dam Risk Assessment Shi Dongmei Yang Fengbao Wang Xiaoxia (College of Information and Communications Engineering,North University of China,Taiyuan 030051,China) To solve the problem that the present risk assessment method of tailings dam does not consider the correlation between monitoring indexes resulting in double calculation during the evaluation process,the correlation between the monitoring indexes is considered and converted them into weights,so that the dominant index had the smaller weight,and vice versa.So the problem of double counting can be lowered.An integrated weighting method was used to determine the weights:according to the characteristics that monitoring indexes has different influence on each other,an influencing matrix is established.As the experts information required in the matrix is fuzzy,the trapezoidal fuzzy number is used to describe experts information and to calculate the subjective weights;With features of fuzziness and randomness,the monitoring data are represented by possibility distributions,then the correlation coefficient weighting method was used to calculate the objective weight of every index;Subjective weight and objective weight are integrated by the mean method.Example results show that:the weight calculation method that considers the coefficient of monitoring indexes can reduce duplication in risk assessment,and integrate subjective and objective weights.This method provides the theoretical basis for weighting of each index for tailings dam. Tailings dam,Risk assessment,Correlation,Influence matrix,Possibility of correlation coefficient weighting method 2014-09-22 山西省高等学校留学回国人员科研项目(编号:201110),山西省研究生优秀创新项目(编号:20123095)。 史冬梅(1987—),女,硕士研究生。 TD77 A 1001-1250(2014)-11-143-04
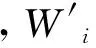


2 实例分析


3 结 语
