顶板崩落变形破坏过程的数值分析
2014-08-08王良唐飞
王 良 唐 飞
(1.中国有色金属工业昆明勘察设计研究院,云南 昆明 650051; 2.云南思茅山水铜业有限公司, 云南 普洱 665000)
顶板崩落变形破坏过程的数值分析
王 良1唐 飞2
(1.中国有色金属工业昆明勘察设计研究院,云南 昆明 650051; 2.云南思茅山水铜业有限公司, 云南 普洱 665000)
采用数值方法建立三维计算模型,分11个步骤对采场开挖的全过程进行数值模拟,得到开挖后空区围岩的水平位移、竖向位移和塑性区分布情况,进而分析矿区顶板自然崩落规律的变形破坏情况。由于采场的开挖,导致岩体内部应力释放,围岩位移指向空区内部,水平位移最大处出现在采场采矿区的两侧边帮处,位移方向均指向采空区内部。随着开挖宽度的扩大,竖向位移呈圆弧曲线形式由采场顶板向岩体内部不断扩张。开挖过程中,空区顶板首先由剪切破坏导致岩体破裂下落,出现采场顶板冒落现象,采场采空区的顶板中央上部岩体随着顶板冒落不断往下变形,出现一定高度破坏区域的岩体。当采场开挖面积进一步扩大时,采场顶板上方的岩块将无法维持稳定状态,出现持续崩落现象。
自然崩落 顶板 变形 破坏
某铜矿资源储量丰富,现保有铜矿石储量3.3亿t,铜金属储量200万t,且矿体产状厚大,但由于矿石品位较低,必须采用采矿成本低、生产能力大、生产效率高的采矿方法才能取得合理的经济效益。从目前设计开采的范围看,矿体厚度基本上都属于厚大矿体,连续性较好,矿岩可崩性属中等,可以形成连续的崩落,在技术上具有适合采用自然崩落法进行开采的一些相关条件。自然崩落法是一种利用重力和相应的地应力作用实现自然落矿的采矿方法[1-4],由于矿体底部的拉底导致该部位岩体应力发生重分布,产生较大拉应力,引起矿石的崩落[5-7]。实际上自然崩落的作用过程是一个十分复杂的岩体工程结构的动态稳定问题,目前岩石力学研究中已有的理论解[8],主要用于圆形或椭圆形洞室等规则形状的问题,但无法对岩体开挖过程中的应力和变形情况进行实时观察。近年来,由于数值模拟方法的不断发展,采用计算机来模拟实际工程情况已成为岩石力学研究的重要手段[9-11],因此,本研究运用数值计算方法进行矿区顶板自然崩落规律的变形破坏情况分析,拟对工程实践提供一定参考。
1 模型介绍
由于矿区天然地质情况极为复杂,在进行分析时需要抓住重点问题,研究主要因素对矿区的影响。因此需要对矿区地质进行简化,从而建立合理的三维地质分析模型进行数值分析。在选取建模的范围时完全考虑边界效应的影响,为了尽可能减小边界效应对计算结果的影响,建模范围区比要研究的问题区大3~5倍,考虑到模型大小的问题,本次取约3倍边界范围大小进行建模,如图1所示,该模型包括岩体闪长玢岩、矿体石英二长斑岩以及开挖采场,模型共66 438个节点,60 400个单元,模型尺寸为1 200 m×600 m×400 m。

图1 矿区三维计算模型Fig.1 Three dimensional calculation model for mine
在地面下-200 m深度处进行开挖,原有硐室尺寸为24 m×24 m×15 m,在水平方向上向四周进行开挖,每次开挖宽度为12 m,即向四周各开挖6 m。预计开挖步数设为11步,以确保在开挖后塑性区完全贯穿到地表。通过计算,当开挖步为9步时,即开挖宽度132 m,岩层的塑性区贯通到地表,程序计算开始不收敛。开挖步骤及情况如图2所示。边界条件为:模型上表面为地表,因此设定边界采用自由边界;由于模型范围足够大,因此设定底部采用固定位移进行约束,4个侧面采用固定法向位移进行约束。
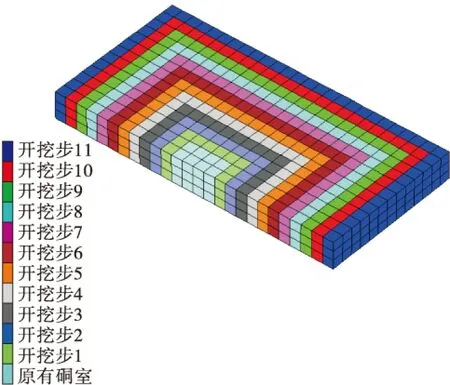
图2 开挖区域局部三维模型Fig.2 Three dimensional model for the local excavation area
2 数值计算结果
2.1 竖直位移变化规律
图3为采场开挖宽度从24 m开挖到132 m过程中开挖区附近由于开挖所引起的竖直位移云图。从图3中可以看出,位移指向空区内部,即空区顶板位移向下,底板回弹隆起,左侧边帮位移向右,右侧边帮位移向左,符合实际情况。
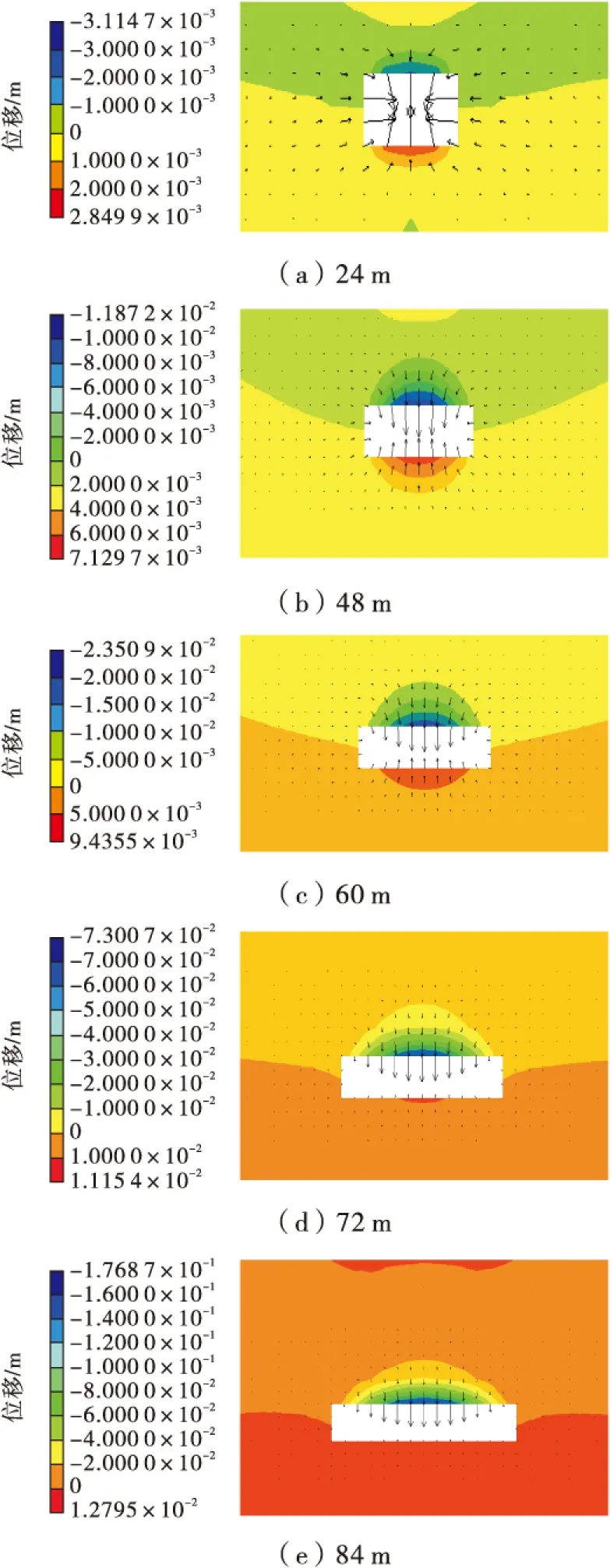
图3 不同开挖尺寸下竖直位移等值云图Fig.3 The vertical displacement contour for different excavation sizes
采场开挖到24 m时,竖向位移最大处出现在采场空区的顶板中央和底板中央部分。采场中央顶板在重力作用下,位移方向向下,最大位移量为3 mm左右,此时采场空间较小,岩体在洞室开挖后,虽然应力场发生了重分布,采空区周围发生了应力释放现象,但由于岩体的自身具有稳定性能力,此时采场相对稳定,因此岩石位移量较小。采场底板中央向上隆起,这是由于洞室开挖导致应力释放,岩体失去了约束,因此向采场内部发生一定的位移。但由于采场空间较小,空间较为稳定,因此底部岩石回弹量较小,与顶部塌落量相仿,最大位移为2 mm左右。采场开挖到48 m时,竖向位移最大处仍然出现在采场空区的顶板中央和底板中央部分。采场顶板中央部位竖向位移逐渐增大,达到1 cm左右,而此时的采场底板中央部位竖向位移虽然也在增大,但是增大幅度要小于顶板竖向位移增大幅度,底板竖向最大位移达到6 mm。这说明,随着洞室开挖面积的不断扩大,采场的临空面不断增加,相比较于地应力来说,此时重力的作用逐渐显现出来,并逐渐成为主要作用因素。矿石在重力的作用下产生塑性变形,开始向下塌落,但只有当开挖宽度到达一定量时,矿石才会持续破坏,产生持续不断的竖向位移,进而发生持续崩落。随着开挖宽度的不断扩大,竖向位移呈圆弧曲线形式由采场顶板向岩体内部不断扩张。当采场开挖宽度达到72 m后,竖向应力的应力减小区扩展到采场的整个顶板,并沿圆弧线向顶板的岩石内部扩展。此时采场底板的竖向位移与顶板竖向位移相比要小的多,顶板的竖向最大位移达到7.3 cm,可判定此时岩石顶板早已经塌落。
2.2 水平位移变化规律
图4为采场开挖区附近由于开挖引起的竖直位移云图。从图4中可以看出,采场采空区水平位移的分布与水平应力分布有关,采场开挖到24 m时,水平位移最大处出现在采场采矿区的两侧边帮处,位移方向均指向采空区内部,这是岩体在洞室开挖后,水平应力场发生了重分布,采空区周围发生了应力释放现象造成的必然结果。并且水平位移最大处处于边帮的中央位置,以采场高度轴线为中心对称分布。说明此时采场空间较小,岩体在洞室开挖后,虽然应力场发生了重分布,采空区周围发生了应力释放现象,但由于岩体的自身具有稳定性能力,此时采场相对稳定,因此岩石位移量较小;同时也可说明当采场开挖面积较小时,由于水平地应力的作用比较明显,而自重应力的作用就稍微影响较小,因此水平位移沿边帮高度轴线中心对称分布,中间大,向上下两侧逐渐减小。当采场开挖宽度从36 m逐渐增加到60 m的过程中,可发现水平位移最大值仍然出现在采场采空区的两侧边帮处,位移方向均指向采空区内部,但位置逐渐由边帮的中央部位向采场顶部移动,尤其发生在顶板和边帮连接的拐角处位置;说明随着采场开挖面积的不断增大,虽然水平应力的作用一直存在并且十分明显,但是由于开挖面积增大而导致的采场临空面增大,使得自重应力的影响逐渐显现出来;从而导致在水平应力和自重竖向应力的共同作用下,采场水平最大位移逐渐向顶板和边帮的拐角处靠拢。当采场开挖宽度大于60 m后,可发现水平位移最大处逐渐转移到采场顶板两侧,靠近边帮的拐角位置,位移方向均指向采空区内部;说明随着采场开挖面积的不断增大,自重应力的影响明显显现出来。采场临空面的进一步扩大导致竖向位移不断增大,并且远大于水平位移,因此在采场顶部的岩石向下塌落时,顶板中央的岩石主要发生竖向位移,而靠近两侧的岩石在塌落过程中水平位移分量大于边帮等地方的水平位移,因此水平位移主要集中在采场顶部的两侧,主要是由于重力引起的塌落造成的。

图4 不同开挖尺寸下水平位移等值云图Fig.4 The horizontal displacement contour for different excavation sizes
2.3 采场塑性破坏区域分布规律
图5表示围岩塑性破坏状态,当采场开挖到24 m时,采场采空区发生塑性破坏的部位主要是采场顶板和底板部位,采场主要破坏模式为剪切破坏。但是由于采场开挖空间和面积较小,因此采空区的塑性破坏区很小。当采场开挖到36 m,采场采空区发生塑性破坏的部位发展到更大的范围,主要是采场顶板、底板部位和两侧边帮。所有的塑性破坏区的破坏模式均为剪切破坏模式。空区顶板主要发生拉剪破坏,但是空区周围的塑性区范围较小,因此可以分析说明此时采场总体情况较稳定,可认为空区顶部岩层发生崩落的几率较小。当采场开挖达到48 m时,采场采空区发生塑性破坏的部位发展到更大的范围,空区顶板主要发生剪切破坏,空区顶板中部同时发生拉伸破坏和剪切破坏,采场顶板岩层破坏模式开始变化,由原来的剪切破坏为主,逐渐变化为以拉伸破坏为主。之后随着采场的开挖面积的不断扩大,采场采空区正上部顶板发生拉伸破坏的范围不断增大,岩石的破坏模式为拉伸破坏的区域从采场的顶板中央逐渐向两侧扩展,最后覆盖整个采场顶板,并呈弧线向采场顶板上方岩体内部扩展,但扩展到一定范围后,岩体的破坏模式又逐渐转变为以剪切破坏为主的塑性破坏模式。当采场开挖宽度达到72 m时,空区正上部顶板基本发生拉伸破坏,并呈弧线向采场顶板上方岩体内部扩展,再往上部分主要发生剪切破坏。随着采场开挖的进行,采场临空面不断增加,采场顶板破坏区域面积也随之明显增大。而采场采空区周围岩体两侧边帮破坏区域主要破坏模式依然是剪切破坏,边帮剪切破坏区域面积较先有所增加。当采场开挖面积进一步扩大时,采场顶板上方的岩块将无法维持稳定不动状态,岩体随着时间不断下落而不是达到稳定状态。岩块下落量随时间较为稳定不变,出现持续崩落现象。
图6为开挖到132 m时塑性区分布的三维图。可见当采场开挖宽度达到132 m时,采场上方的塑性破坏区域与地面上方的塑性破坏区域贯通到一起,计算出现了较为明显的不收敛。此时塑性破坏区域贯通到地表,矿体岩层整体塑性破坏下陷,视为岩体完全失稳。


图5 不同开挖尺寸下塑性区分布Fig.5 The plastic zone distribution for different excavation sizes

图6 开挖到132 m塑性区分布3D效果图Fig.6 3D effect of plastic zone distribution when excavated to 132 m
2.4 采场塑性破坏区岩层崩落规律
通过自编程序计算出塑性区的体积,分析开挖过程中采场周围塑性破坏区域的数量和发展速度。图7为开挖宽度与塑性区体积之间的关系图,可见,开挖过程中塑性区体积增量明显分为3个阶段,第一阶段为采场开挖宽度在48 m以下时,矿层的塑性区体积增加量十分小,基本保持不变,该区可称为稳定区,可认为此时岩层崩落量很小;第二阶段为采场开挖宽度在48 m以上时,矿层塑性区的体积量稳定均匀增加,该区可称为持续崩落区,在此区间矿层崩落速度均匀稳定;第三阶段为采场开挖宽度增加到132 m时,矿层塑性区的体积量迅速增加,速度不断加快,该区可称为破坏区,可认为该区间矿层崩落速度不能控制,塑性区迅速增加,塑性区贯通到地面,导致地面发生沉降。
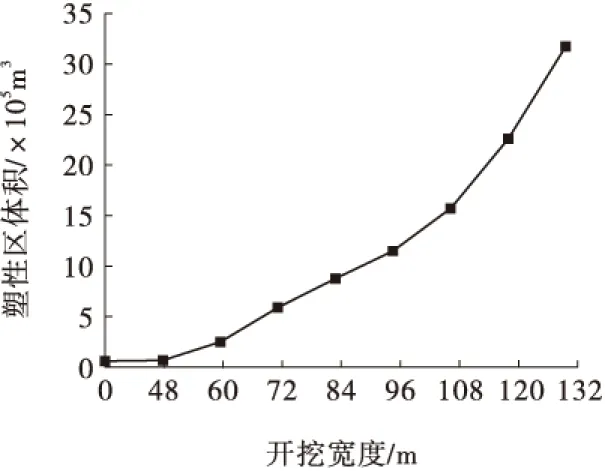
图7 采场开挖宽度与塑性区体积关系图Fig.7 Relation between the excavation width and the volume of plastic zone
3 结 论
(1)由于采场的开挖,导致岩体内部应力的释放,岩石的位移指向空区内部,水平位移最大处出现在采场采空区的两侧边帮处,位移方向均指向采空区内部。随着开挖宽度的不断扩大,竖向位移呈圆弧曲线形式由采场顶板向岩体内部不断扩张。当采场开挖宽度达到72 m后,竖向应力的应力减小区扩展到采场的整个顶板,并沿圆弧线向顶板的岩石内部扩展。
(2)开挖过程中,空区顶板首先由于剪切破坏导致岩体破裂下落,出现采场顶板冒落现象,采场采空区的顶板中央上部岩体随着顶板冒落也不断往下变形,从而出现一定高度的破坏岩体,此部分岩体以上部分由于应力重分布及其以下岩体冒落完毕而处于稳定状态。当采场开挖面积进一步扩大时,采场顶板上方的岩块将无法维持稳定不动状态,岩体随着时间不断下落而不是达到稳定状态。当采场开挖宽度达到132 m时,岩块下落量随时间较为稳定不变,出现持续崩落现象。
[1] 高文德,王文星.丰山铜矿自然崩落法的试验研究[J].矿业研究与开发,2003,23(1):9-11. Gao Wende,Wang Wenxing.An experimental study on the block caving system in Fengshan Copper Mine[J].Mining Research and Development,2003,23(1):9-11.
[2] 姜增国,杨保仓.基于DDEM的自然崩落采矿法崩落规律的数值模拟[J].岩土力学,2005,26(2):239-242. Jiang Zengguo,Yang Baocang.Numerical simulation of caving law in natural caving mining method based on deformable discrete element method[J].Rock and Soil Mechanics,2005,26(2):239-242.
[3] 王家臣,陈忠辉,熊道慧,等.金川镍矿二矿区矿石自然崩落规律研究[J].中国矿业大学学报,2000,29(6):46-50. Wang Jiachen,Chen Zhonghui,Xiong Daohui,et al.Research on natural caving regularity of ore in No.2 Mining Area in Jinchuan Nickel Mine[J].Journal of China University of Mining & Technology,2000,29(6):46-50.
[4] 王连庆,高 谦,王建国,等.自然崩落采矿法的颗粒流数值模拟[J].北京科技大学学报,2007,29(6):557-561. Wang Lianqing,Gao Qian,Wang Jianguo,et al.Numerical simulation of natural caving method based on particle flow code in two dimensions[J].JournaI of University of Science and Technology Beijing,2007,29(6):557-561.
[5] 马春德,李夕兵,陈 枫,等.自然崩落法矿山深部地应力场分布规律的测试研究[J].矿冶工程,2010,30(6):10-14. Ma Chunde,Li Xibing,Chen Feng,et al.Research on in-situ stress distribution in deep mine with natural caving method[J].Mining and Metallurgy Engineering,2010,30(6):10-14.
[6] 张东红.自然崩落法的岩石力学工作与矿石崩落块度[J].矿业研究与开发.2003,23(S1):86-87. Zhang Donghong.Rock mechanics of block caving method and ore-caved fragmentation[J].Mining Research and Development,2003,23(S1):86-87.
[7] 袁海平,吴祥松,温广军.流变断裂型矿岩自然崩落速率模拟预测[J].采矿与安全工程学报.2008,25(3):341-346. Yuan Haiping,Wu Xiangsong,Wen Guangjun.Prediction for block caving velocity of rheologic fracture ore rock[J].Journal of Mining & Safety Engineering,2008,25(3):341-346.
[8] 王文星.岩体力学[M].长沙:中南大学出版社,2004. Wang Wenxing.Rock Mechanics[M].Changsha:Central South University Press,2004.
[9] Alejano L R,Ferrero A M,Ramírez-Oyanguren P,et al.Comparison of limit-equilibrium,numerical and physical models of wall slope stability[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(1):16-26.
[10] Bahaaddini M,Sharrock G,Hebblewhite B K.Numerical investigation of the effect of joint geometrical parameters on the mechanical properties of a non-persistent jointed rock mass under uniaxial compression[J].Computers and Geotechnics,2013,49:206-225.
[11] Cai M.Influence of intermediate principal stress on rock fracturing and strength near excavation boundaries:insight from numerical modeling[J].International Journal of Rock Mechanics and Mining Sciences,2008,45(5):763-772.
(责任编辑 石海林)
Numerical Analysis for the Deformation Failure Process of Roof Caving
Wang Liang1Tang Fei2
(1.ChinaNonferrousMetalsIndustrySurveyandDesignInstituteinKunming,Kunming650051,China;2.YunnanSimaoShanshuiCopperCo.,Ltd,Puer665000,China)
Numerical method is used to build a three-dimensional calculation model for numerically simulating the whole excavation procedure in the stope by 11 steps.By this method,the distribution of horizontal displacement,vertical displacement and plastic zone of surrounding rock in mined-out area after excavation is obtained and then the deformation and failure of the natural roof caving in the mining area is analyzed.The excavation of the stope leads to the release of internal stresses in rock mass,and the displacement of rock mass directs to the internal part of goaf.Maximum horizontal displacement occurs at the two sides of mining area in the stope and it directs to the internal part of goaf.With the expansion of the excavation width,the vertical displacement expands from the stope roof to the inside of rock mass in the form of arc curve.During the excavation,the rock of goaf roof falls due to the shear failure,therefore,the roof caving occurs.And the rock mass in the upper central part of the goaf roof deforms downward continually with the roof caving happening,hence,a certain height of damaged rock mass occurs.When the area of excavation expands further in the stope,rocks above the stope roof will not remain stable and continue to fall down.
Natural caving,Roof,Deformation,Failure
2014-05-18
王 良(1971—),男,高级工程师,国家一级注册建造师。
TD325
A
1001-1250(2014)-10-037-05
