捕食者具有厌食性反应且食饵具有Allee 效应的捕食系统
2014-08-08王文婷王万雄
王文婷, 王万雄
(1. 兰州交通大学数理与软件工程学院, 兰州 730070; 2. 甘肃农业大学理学院, 兰州 730070)
捕食者具有厌食性反应且食饵具有Allee 效应的捕食系统
王文婷1, 王万雄2,*
(1. 兰州交通大学数理与软件工程学院, 兰州 730070; 2. 甘肃农业大学理学院, 兰州 730070)
在Dubis动力系统的基础上,建立了具有Allee效应的捕食系统模型。对系统的稳定性进行了分析,受Allee效应的影响,食饵种群可能因为种群大小处于临界点以下而趋于灭绝。通过对系统进行模拟,结果表明:不受Allee效应的影响,系统的演化属于一种理想化的情形系统到达P(平衡)点的时间较不受Allee效应影响时系统到达P点的时间短,不利于生物的进化,而在Allee效应的影响下,系统的演化将达到一个平衡状态。由此,说明Allee效应为濒临灭绝物种的管理提供了重要的理论依据,对管理部门的决策有参考指导作用。
Allee效应;平衡点;稳定性;捕食系统;厌食性指标
随着人类社会活动强度的日益增加,在工业化、全球化、一体化的同时,生态坏境也在不经意间遭到破坏,对生物的生存产生不利影响。对小种群而言,更容易受到Allee效应的影响。 Allee在1931年指出:群聚有利于种群的增长和存活,但过分稀疏和过分拥挤都可能阻止生长,并对生殖发生负作用,以至走向灭绝。每种生物发展都有自己的最适密度[1],Allee效应对生物进化也起到一定作用,它在一持续资源轴上对种类集群有重要性[2]。这方面的理论探讨和实验观测一直是种群生态学研究上的热点之一。同时,随着人们对空间生态学研究中重要性的认识,生态学家们正尝试把Allee效应这一生态现象的研究拓展到更广的空间尺度上去[3]。
1975年,Dubis等人研究了下述系统:
(1)
式中,当x≤τ时,k(x)=k2(x);当x>τ时,k(x)=k2τ.这里α,β,τ,k1,k2均为正常数,利用计算机模拟发现系统可以存在两个极限环,但未给出证明;随后,刘南根和陈均平[4- 5]等分别研究了具有Ι型功能反应的捕食系统,且证明了两个极限环的存在性;文献[6]分析了Allee效应对几何种群同步性的影响,文献[7]建立了具有Allee效应的食饵-捕食者模型,讨论了强Allee效应和弱Allee效应对食饵种群的影响以及模型解的有界性和各平衡点的存在性,文献[8]讨论了一类具有弱Allee效应的捕食-食饵模型献,文献[9]利用微分不等式和通过构造适当的Lyapunov函数,讨论了一类既具有反馈控制又具有厌食反应和疾病传染的周期捕食系统的持续生存性以及周期解的存在性,唯一性和稳定性问题,而文献[10]考察了当食饵具有种群防御能力的Ι型功能性反应的如下动力系统(称之为Ι型厌食系统)。

(2)
文献[7]讨论了具有Allee效应的如下系统模型
(3)
式中,x表示捕食者的密度,y表示捕食者的密度,m表示捕食系数[11],A为Allee阈值,e为转系数。由此,进一步说明了,Allee效应对生物动力学系统有重要影响。
基于学者们的这些工作,本文将对捕食者具有厌食性指标且食饵具有Allee效应的捕食系统进行研究。
1 模型的建立于平衡点稳定性的分析
本文建立了Ι型功能性反应的如下动力系统:
(4)
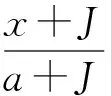
(5)
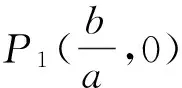
当x>β时,h(x)=cβ2/x;系统(4)化为:
(6)
对于系统(6)进行运算,得出系统的平衡点:

将对各平衡点的稳定性进行分析,对系统(5)进行求导得到Jacobi矩阵:
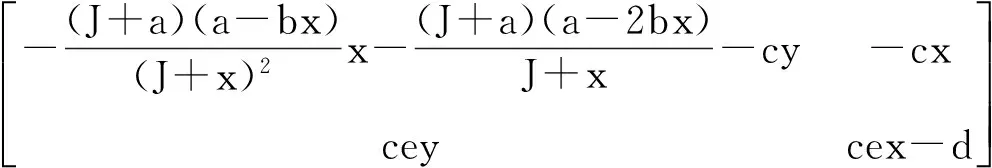
在p0(0,0)点处,系统是不稳定的。

应用Routh-Hurwitz判据,λ1+λ2<0,λ1·λ2>0,(下同各平衡点判断方法)则平衡点P1是稳定的,即捕食者最终灭亡(图1)。

则平衡点P2是稳定的,即食饵和捕食者两种群共存,并且最终达到稳定状态(图2)。
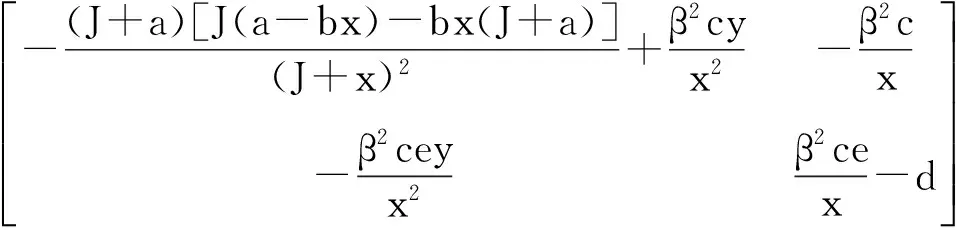
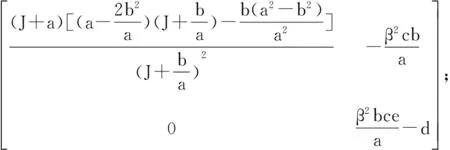
由此,应用Routh-Hurwitz判据,平衡点P3是不稳定的,即捕食者最终灭亡(图3)。
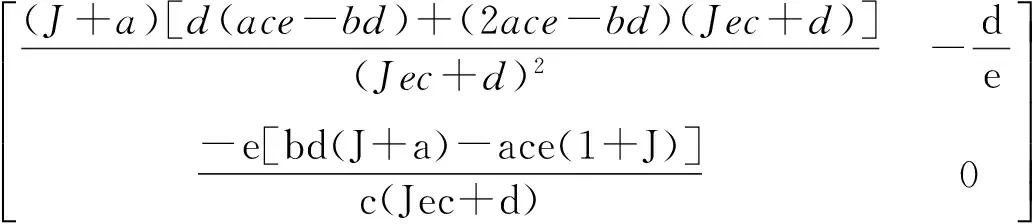
对应的特征根方程为:
则平衡点P4是稳定的,即食饵和捕食者两种群共存,并且最终达到稳定状态(图4)。
2 模拟与讨论
2.1 利用Matlab软件对系统在各平衡点处的动态进行模拟(结果分别如下各图所示)
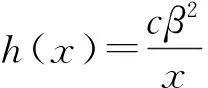

图1 当h(x)=cx时,平衡点P1处,捕食者灭亡,系统最终达到稳定状态 Fig.1 When h(x)=cx, at Equilibrium point P1,the predator go extinct, the system is become stabilized时间Time为单位时间
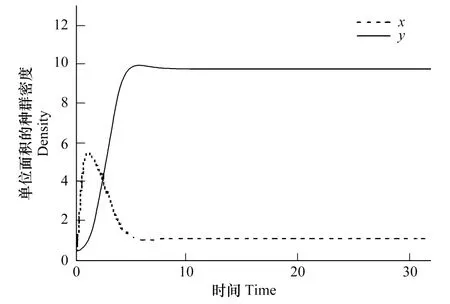
图2 当 h(x)=cx时平衡点P2处,食饵和捕食者两种群共存,并且最终达到稳定状态Fig.2 When h(x)=cx,at Equilibrium point P2 the predator and the prey coexist with each other,the system is become stabili
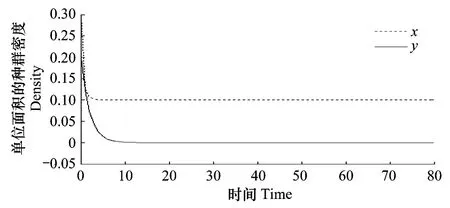
图3 当时平衡点 P3处,捕食者灭亡,系统最终达到稳定状态Fig.3 When ,at equilibrium point P3,the predator go extinct,the system is become stabilize

图4 当 时平衡点处P4,食饵和捕食者两种群共存,并且最终达到稳定状态Fig.4 When ,at equilibrium point the predator P4 and the prey coexist with each other, the system is become stabilize
2.2 利用Matlab软件对系统未受Allee效应影响与受Allee效应影响的系统稳定性的相图进行模拟比对
图5为h(x)=cx时时,即x≤β时,系统(5)的图, 受Allee 影响的系统的稳定性的相图 。
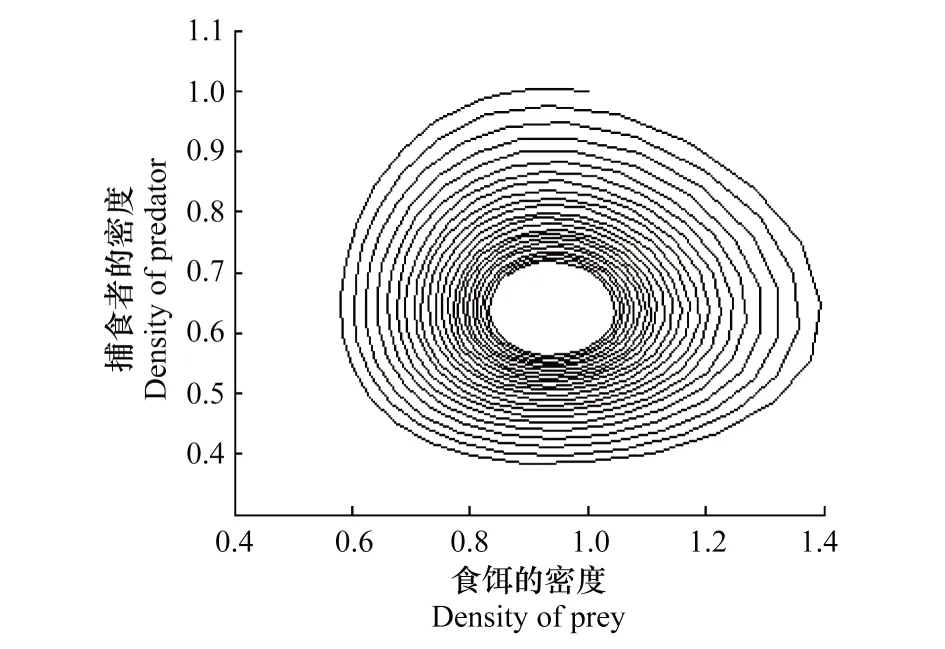
图5 系统(5)受Allee效应的影响,食饵与捕食者的演化相图Fig.5 With Allee effect, the evolution phase of prey and predator
图6为h(x)=cx时时,即x≤β时,系统(5)的图, 未受Allee 影响的系统的稳定性的相图。
(1)基于油茶花期构建的产量模型平均相对误差为19%,增减差准确率为75%,产量模型能很好地模拟出实际油茶产量的变化趋势,利用花期产量模型能很好地预测来年油茶产量,为油茶防灾减灾提供决策依据。
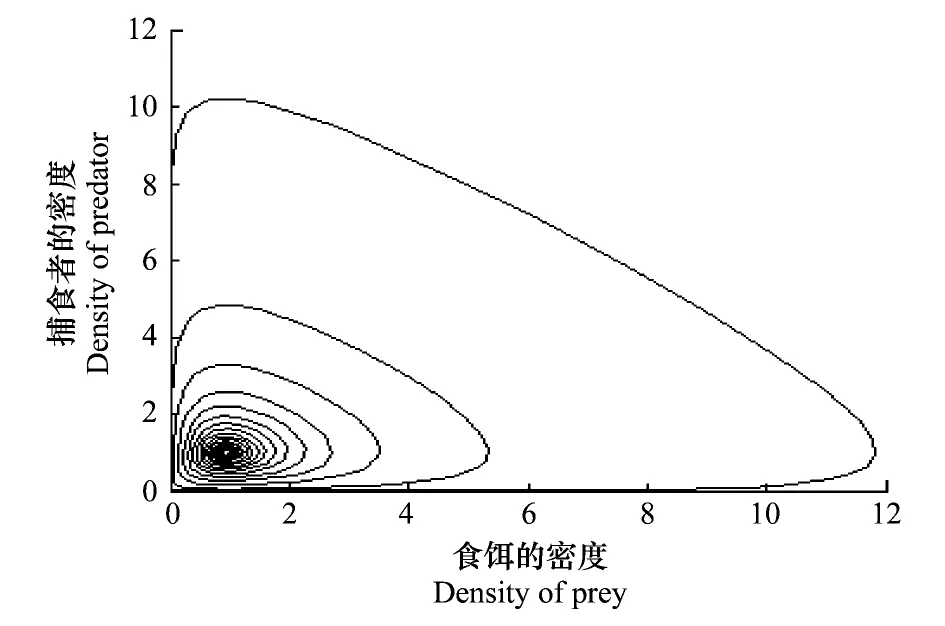
图6 系统(5)未受Allee效应的影响,食饵与捕食者的演化相图Fig.6 Without Allee effect, the evolution phase of prey and predator
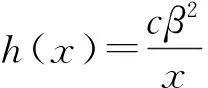

图7 系统(6)未受Allee效应的影响,食饵与捕食者的演化相图Fig.7 Without Allee effect,the evolution phase of prey and predator
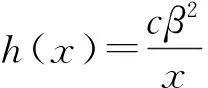
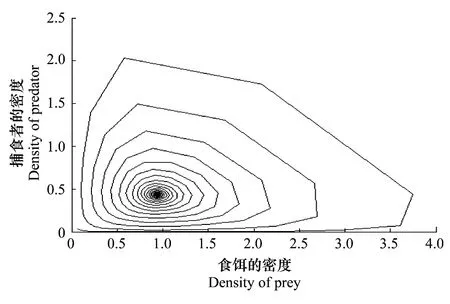
图8 系统(6)受Allee效应影响下,食饵与捕食者的演化相图Fig.8 With Allee effect, the evolution phase of prey and predator
2.3 讨论
图1,图2描述了当h(x)=cx即x≤β(食饵种群密度小于等于厌食性指标)时,捕食者与食饵随时间的演化过程。由图1可见,在t=3的单位时间内,随食饵种群数量减少,捕食者数量减少,到t=6的单位时间时,捕食者的种群数量趋于灭绝,系统最终达到稳定状态。由图2可知,在0 图5,图6分别给出了当h(x)=cx即x≤β时,捕食者与食饵在演化过程中的相图。 由图5图6可知,未受Allee效应影响捕食系统中食饵与捕食者的演化相图趋于一个圆形,且等切线分布均匀,波动不大,而受Allee效应影响捕食系统中食饵与捕食者的演化相图类似于一个不规则的扇贝形,等切线分布不均匀,波动较大,则捕食者与食饵种群密度的变化起伏很大,那么这时,系统达到平衡状态的时间要多于未受Allee效应影响的系统到达平衡状态所用的时间。 由图7图8可知,未受Allee效应影响捕食系统中食饵与捕食者的演化相图趋于一个均匀分布的椭圆,且等切线分布均匀,波动不大,而受Allee效应影响捕食系统中食饵与捕食者的演化相图类似于一个不规则的扇贝形,等切线分布不均匀,波动较大,则捕食者与食饵种群密度的变化起伏很大,那么这时,系统达到平衡状态的时间要多于未受Allee效应影响的系统到达平衡状态所用的时间。 系统未受Allee效应的影响时,相比系统受Allee相应的一项,未受Allee效应影响(即不受任何外界影响)的系统的演化是比较理想的,在实际生活应用中,不具有现实意义。在开始阶段,捕食者与食饵种群的密度起伏都较小。随着Allee效应的影响,过了一段时间后,系统的达到一个新的平衡,破坏了原先的物种的平衡状态。受Allee效应影响的系统延迟了系统未受Allee效应影响的达到平衡状态所需的时间。 本文研究了I型功能性反应函数的系统模型,通过Matlab软件对系统进行模拟研究,给出了受Allee效应影响与未受Allee效应影响的捕食者与食饵的演化相图。 结果表明,未受Allee效应的影响,系统的演化属于一种理想化的情形,不利于生物的进化,而在Allee效应的影响下,系统的演化将比未受Allee效应影响的系统到达平衡状态所需要的时间长,所以考虑了Allee效应的系统模型更为合理。如果一个种群收到Allee效应的影响,即种群的数量低于一定值时,由于寻找配偶的困难,社会性功能异常(例如保护幼体,觅食,警戒分工等),近交衰退等原因导致种群增长率减少甚至出现负增长[12- 14],Allee效应为濒临灭绝物种的管理提供了重要的理论依据,对管理部门的决策有参考指导作用。 [1]AlleeWC,EmersonAE,ParkO.PrinciplesofAnimalEcology.PhiladelphiaPA:WBSaunders, 1949. [2] Dubois D M. Primary and secondate production in the southern, Bight;A Mathematical Theory // Proceeding of the 10thEuropean Symposium on Marine Biology, Ostend, Vniversa Press ED by Presoome and Jaspers. 1975, 2: 211- 229. [3] Liu N G. The limit-cycle of predator-prey system with Holling I functional response. Chinese Annals of Mathematics, Series A, 1988, 9(4): 421- 427. [4] Chen J P, Ma H D. The qualitative analysis of two species predator-prey model with holling′s type Ⅲ functional response. Applied Mathematics and Mechanics, 1986 7(1): 73- 80. [5] Wang L L, Fan Y H, Quan H S. Ⅰ Functional response prey-predator system while the prey population has group defense ability. Journal of Lanzhou University: Natural Sciences, 2000, 36(5): 24- 29. [6] González-Olivares E, Rojas-Palma A, Rojas-Palma A, Flores J D. Dynamical complexities in the Leslie-Grower predator-prey model as consequences of the Allee effect on prey. Applied Mathematical Modelling, 2011, 35(1): 366- 381. [7] Wang W D. Persistence in a discrete model with delays. Journal of Southwest China Normal University: Natural Science Edition, 1992, 17(1): 13- 18. [8] Dieckmann U, Marrow P, Law R. Evolutionary cycling in predator-prey interactions, population dynamics and the red queen. Journal of Theoretical Biology, 1995, 176(1): 91- 102. [9] Liu Z G, Zhao X, Zhao F P, Chen A M. Allee effects of local populations and the synchrony of metapopulation. Acta Ecologica Sinica, 2012, 32(1): 1- 6. [10] Ma Z N, Zhou Y C, The stability theory of ordinary differential equations. Beijing: science press,2001. [11] Fu X Y, Zhang Y J, Liu C, Li Y K. The stability o f predator-prey systems subject to the Allee effects. Journal of Biomathematics, 2012, 27(4): 639- 644. [12] Chenille C, Huang Z K. Persistence and periodic solution in prey-predator system with feedback controls,anorexia and infection response. Journal of Shangqiu Teachers College, 2006, 22(1): 57- 60. 参考文献: [3] 刘南根. 具Holling′I型功能反应的食饵-捕食系统的极限环. 数学年刊(A)辑, 1988, 9(4): 421- 427. [4] 陈均平, 马洪德. 具功能性反应的食饵-捕食者两种群模型的定性分析. 应用数学与力学, 1986, 7(1): 73- 80. [5] 王琳琳, 樊永红, 权宏顺. 食饵种群具有群体防御能力的I类功能性反应的捕食系统. 兰州大学学报: 自然科学版, 2000, 36(5): 24- 29. [7] 王稳地. 一个带时滞的离散模型的一致持续生存. 西南师范大学学报: 自然科学版, 1992, 17(1): 13- 18. [9] 刘志广, 赵雪, 张丰盘, 陈爱敏. 局域种群的Allee效应和集合种群的同步性. 生态学报, 2012, 32(1): 1- 6. [10] 马知恩, 周义仓. 常微分方程定性与稳定性方法. 北京: 科学出版社, 2001. (未链接到本条文献英文信息) [11] 付晓阅, 张玉娟, 刘超, 李元可. 具有Allee效应的食饵—捕食者模型的稳定性分析. 生物数学学报, 2012, 27(4): 639- 644. [12] 陈超, 黄振坤. 既具有反馈控制又具有厌食反应和疾病传染的捕食系统的持续生存性与周期解. 商丘师范学院学报, 2006, 22(1): 57- 60. The study for predator-prey system with Allee effect exist on prey and apositic reaction exist on predator WANG Wenting1, WANG Wanxiong2,* 1MathematicsDepartmentofLanzhouJiaotongUniversity, 730070Lanzhou,China2SciencesDepartmentofGansuAgriculturalUniversity, 730070Lanzhou,China Evolution takes place in an ecological setting that typically involves interactions with other organism. Predator-prey interactions are ubiquitous in nature. Such interactions have motivated various theoretical models of phenotypic coevolution in prey-predator communities. One considered the ecological model was the Dubis predator-prey model without Alee effect. However, sometimes the prey population may have a decrease in per capita growth rate at low-density populations. In other word that is Allee effect results in the existence of a threshold density below which the population goes extinct. At low density, fecundity may decrease while mortality may increase because of a range of factors including difficulties in finding mates, social dysfunction and inbreeding depression. These demographic changes lead to negative population growth rates and ultimately push the population extinction. Many studies have demonstrated the potential importance of Allee effects for dynamics of small population, range expansion, community composition and biological invasion. It is widely accepted that Allee effects may increase the extinction risk of low density populations. Evolution suicide is likely outcome of the process[4]. Therefore, it is important to study the coevolution of the phenotypes of predator and prey population subjected to Allee effects. Based on the system of Dubis, we formulate a Predator-prey model which the prey population has Allee effect. For the reason of Allee effect, the prey population will become extinct. Meanwhile we use Matlab made an analog on predator-prey system and get a conclusion on the influence of Allee effect. The system without Allee Effect is too sublimate to apply to the actual life and compare to the system without Allee effect, the system with Allee effect shortens the time of reaching stabilization. By simulating the phase field, we can see the system with Allee effect has very obvious differences than the system without Allee effect. The figure of the system with Allee effect likes a round but the figure of the system without Allee effect gets close to fanshaped. At the same time, the curve has fluctuated on the later, so the densities of predator and prey rise and fall. Such that we can get some enlightenment protecting biological environment.Our study suggests that Allee effect has unstabilizing effect on population dynamics. Therefore, Allee effect has a great influence on endangered species and the research strong theoretical demonstrations on making decisions to protect the engendered population by the authority. Allee effect; equilibrium point; stability; predator-prey system;apositic index 甘肃省自然科学基金资助(1010RJZA127); 科技部支撑项目(2007BAD88B07) 2012- 12- 20; 网络出版日期:2014- 03- 04 10.5846/stxb201212201834 *通讯作者Corresponding author.E-mail: wangwx@gsau.edu.cn;gsplwwt1221@126.com 王文婷,王万雄.捕食者具有厌食性反应且食饵具有Allee 效应的捕食系统.生态学报,2014,34(16):4596- 4602. Wang W T, Wang W X.The study for predator-prey system with Allee effect exist on prey and apositic reaction exist on predator.Acta Ecologica Sinica,2014,34(16):4596- 4602.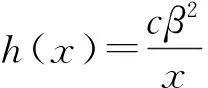
3 结论
