斑膜合垫盲蝽若虫在国槐上的空间分布型及抽样技术
2014-08-08朱惠英吴建华王新东常承秀
朱惠英,沈 平, 吴建华,王新东,常承秀, 田 炜
(1. 甘肃省临夏回族自治州森林病虫害防治检疫站,临夏 731100;2. 甘肃省临夏回族自治州农业学校,临夏 731100)
斑膜合垫盲蝽若虫在国槐上的空间分布型及抽样技术
朱惠英1,沈 平1,*, 吴建华2,王新东1,常承秀1, 田 炜1
(1. 甘肃省临夏回族自治州森林病虫害防治检疫站,临夏 731100;2. 甘肃省临夏回族自治州农业学校,临夏 731100)
斑膜合垫盲蝽Orthotylus(O.)sophoraeJosifov是近年来临夏地区国槐SophorajaponicaLinnaeus上严重发生的害虫之一。应用6种分布型指数法分析判定了斑膜合垫盲蝽若虫在国槐上的空间分布型,利用Taylor幂法则和Iwao回归方程分析聚集原因,结果表明,斑膜合垫盲蝽若虫在国槐上呈聚集分布,公共kc值为0.6169,且符合负二项分布;其种群聚集是由某些环境作用引起的。在此基础上,采用Iwao的方法确定了斑膜合垫盲蝽若虫的田间最适抽样数和序贯抽样表;并根据Gerrard的零频率模型建立了估计该种群平均密度的零频率公式:x=1.7457(-lnP0)1.1119。
斑膜合垫盲蝽;空间分布型;抽样技术
斑膜合垫盲蝽Orthotylus(O.)sophoraeJosifov, 属半翅目Hemiptera,盲蝽科Mlridae,合垫盲蝽属 Orthotylus[1]。在国内分布于四川省、河南省、甘肃省、陕西省、湖北省、天津市,近年来在临夏地区国槐SophorajaponicaLinnaeus 上发生危害,1年发生1代,6月下旬成虫开始交尾产卵,块产,以卵在国槐主干树皮缝内及2—3年生分枝处丝织的巢内越冬;翌年4月下旬开始孵化。以成虫、若虫聚集于新梢叶背刺吸为害,叶面呈现失绿斑点,致使叶片皱缩干枯,叶柄下垂提前脱落。Josifov[1]根据朝鲜的标本形态描述该种,刘国卿[2]报道斑膜合垫盲蝽为中国新记录种;目前,国内外尚无有关斑膜合垫盲蝽生态学方面的研究报道。2011年对斑膜合垫盲蝽若虫在国槐上的空间分布型进行了调查,在此基础上,提出了操作简便、快捷的田间抽样设计方案,确定出能够在允许误差和可信区间范围内对总体参数进行估计的样本数据,为获取准确、系统的虫情调查资料提供了依据。
1 材料与方法
1.1 试验地概况
调查样地位于兰郎公路临夏市西川段(安多园—后杨村口),该路段距离10km,海拔1917.2m,2011年年均气温7.8℃,年日照时数2171.3h,无霜期144d以上,年降水量378mm;栽植地土质坚硬、贫瘠,顺其生长,管理粗放,整体树势衰弱,东西走向,单排栽植,树龄20n,树高5—6m,株距5m,调查前未进行药剂防治。
1.2 取样方法
2011年6月上旬,采用线路调查法,在公路北侧每间隔50m设1样段,共设12组样段;样段内每隔1株取1样株,每样段调查10株;每样株从东、西、南、北4个方位,每方位上、中、下分层随机选1年生枝条为样枝,每样枝调查长度为10cm,分别统计不同方位样枝上的若虫和叶片数。
1.3 分布型测定
根据调查数据,计算均值(若虫数/叶)(m)、方差(s2)、平均拥挤度 (m*)。依据Lloyd聚块性指数(m*/m)、Beall扩散系数(c)、Waters负二项分布k值、森下正明扩散型指数(Iδ)、David和Moore丛生指数(I)、Cassie聚集度指数(Ca)参数标准判定空间分布型[3- 4]。
1.4 聚集原因检验
利用Taylor幂法则[5]和Iwao的m*-m回归模型[6],测定种群的分布格局和内部结构;以Blackith种群聚集均数λ分析聚集原因[3]。
1.5 抽样方法
根据Iwao最适理论抽样数模型[4]计算最适抽样数;应用Iwao的方法[4]确定序贯抽样表;依据Gerrard等的零频率模型[9]估计种群密度和理论抽样[10]。
1.6 数据统计分析
采用Excel2003进行数据统计,参数均采用最小二乘法估计,并利用相关系数r进行相关性检验。
2 结果与分析
2.1 分布型检验
依据斑膜合垫盲蝽若虫12组样段的均值(m)、方差(s2)和平均拥挤度(m*),计算出各样段的聚块性指数(m*/m)、扩散系数(c)、扩散型指数(Iδ)均大于1,丛生指数(I)、聚集度指数(Ca)大于0(表1),根据各参数空间分布型判定标准[3- 4],得出斑膜合垫盲蝽若虫在国槐上呈聚集分布。
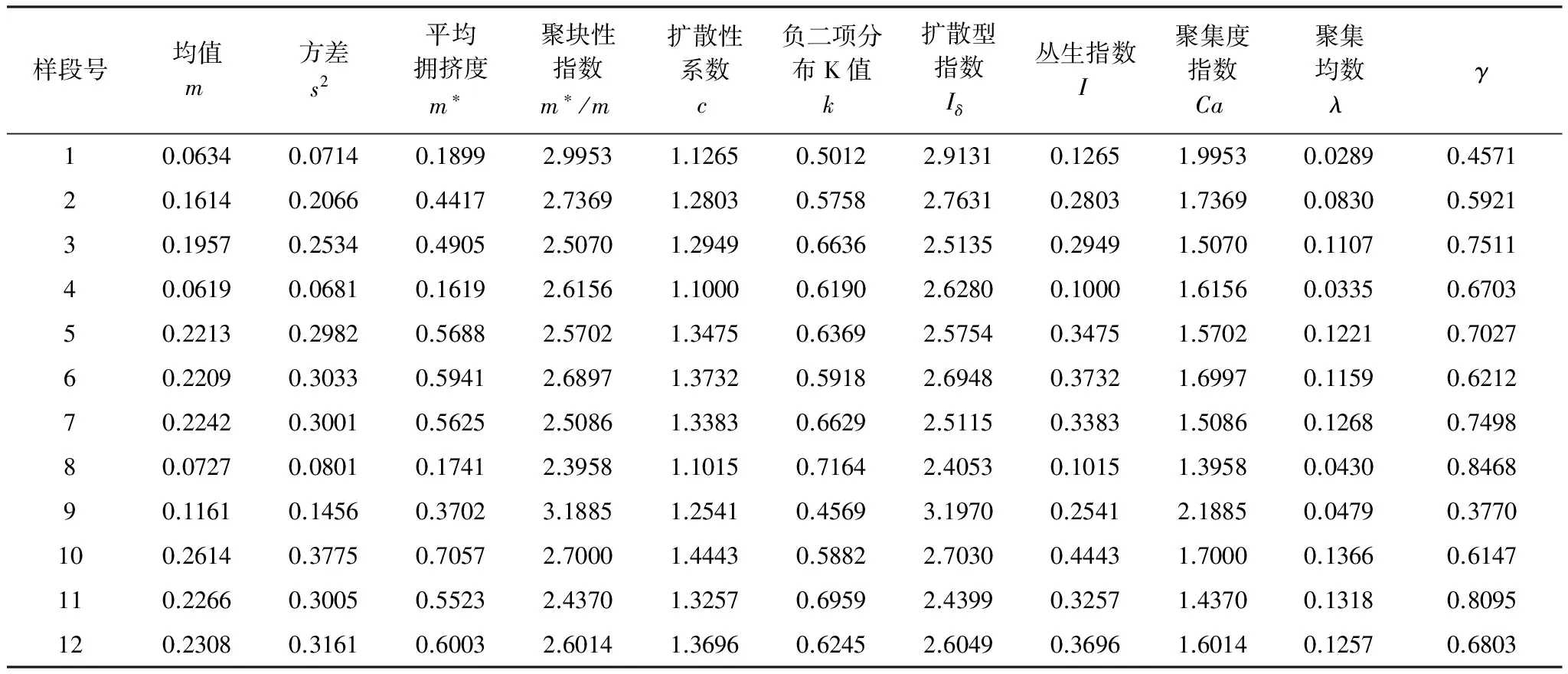
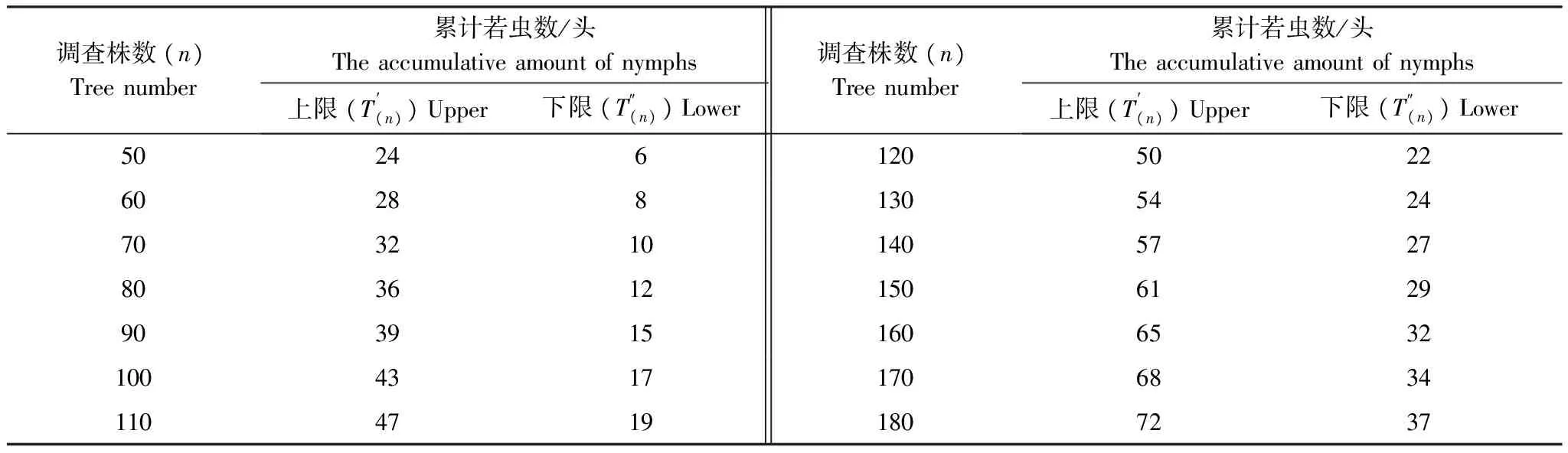
Waters认为,k值与虫口密度无关,k值愈小,种群的聚集度愈大,若k值趋于∞时(一般在8以上时),则逼近Poisson分布[7]。表1中的k值均依据矩法求得,且0 2.2 聚集原因分析 式中, lgα=0.2249>0,b=1.1622>1,s2=1.0274m1.1622,说明种群在一切密度下均是聚集分布,且具密度依赖性,聚集强度随种群密度的升高而增强。 表1 斑膜合垫盲蝽若虫聚集度指标 应用Blackith种群聚集均数λ=mγ/2k分析聚集原因[3]。 式中,m为平均虫口密度,k为负二项分布的指数,γ是自由度等于2k,以0.5概率值对应处的χ2值,应用内插法得出。经计算,12组样段的总λ=0.0922,因此根据Blackith对昆虫的聚集原因分析可知:λ=0.0922<2,说明斑膜合垫盲蝽若虫聚集可能是由某些环境作用引起的。 2.3 抽样技术 2.3.1 理论抽样数技术 应用Iwao最适理论抽样数模型N=(t/D)2[(α+1)/m+β-1][4],确定出最适抽样数公式:N=(t/D)2(1.0224/m+1.5011) 取t=1.96(置信概率为0.95),相对误差(D=d′/m)为0.1、0.2和0.3时,平均若虫数(m)在0.5、0.10、0.15、0.20、…、0.80的条件下,得出斑膜合垫盲蝽若虫的最适抽样数(N)(表2)。 表2 斑膜合垫盲蝽若虫理论抽样数 由表2可知,在相对误差(D)固定时,斑膜合垫盲蝽若虫的最适抽样数(N)随平均若虫数(m)的增大而下降,只是下降幅度逐渐缩小;在相同的平均若虫数(m)下,随着相对误差(D)的增大,所需抽样数(N)依次减少。 2.3.2 序贯抽样技术 用上述两式,计算出斑膜合垫盲蝽若虫序贯抽样表(表3)供防治参考。 d为m=m0时估计密度所允许的置信限,当d=0.1时,最大抽样数为170株;d=0.2时,最大抽样数为42株。 表3 斑膜合垫盲蝽若虫序贯抽样表 2.3.3 零频率估计法 根据Gerrard等的零频率回归模型:x=α(-lnP0)b[9],得出膜合垫盲蝽若虫的平均密度(x)与零频率(P0)回归模型: x=1.7457(-lnP0)1.1119 根据Gerrard的方法对种群进行理论抽样(n)[10],其公式为: n=β2(1-P0)/[P0(-lnP0)2(D)2] 式中,β为模型中-lnP0的指数,P0为零频率,D抽样精度。已知P0=0.8715,D=0.2时,理论抽样数(n)为240.9,即需要调查241片叶是否有虫,求得P0值后代入Gerrard模型x=1.7457(-lnP0)1.1119,即可得出每叶的虫口密度。 将田间按理论抽样数(n)调查取得的P0值代入已知Gerrard模型进行验证,得出理论值x与实测值m的比较结果(表4)。 表4 Gerrard模型理论值与实测值的比较1) 由表4可见,该模型的抽样精度除样段2略大于预定D值0.2,其余11个样段均小于预定D值0.2。因此利用Gerrard模型x=1.7457(-lnP0)1.1119,根据0—1抽样所得P0值,可有效估计国槐叶片上膜合垫盲蝽若虫的种群密度。 本文就斑膜合垫盲蝽若虫的12组样段的调查结果进行了空间分布型检验分析,结果表明,斑膜合垫盲蝽若虫在田间呈聚集分布;其公共kc值为0.6169,符合负二项分布;聚集原因是由某些环境作用引起的;这主要是由于斑膜合垫盲蝽若虫对国槐为害部位(新梢叶背)的选择性所致,其基本上受国槐新梢长势的影响,趋向于阳面树冠外围的新梢。 在虫情调查时,以叶片为抽样单位,在应用本文抽样技术研究确定的模型时,采用随机抽样,因为模型建立的基础是随机抽样。利用本研究确定的斑膜合垫盲蝽若虫理论抽样数,根据精确度与工作量,在允许误差和可信区间范围内,即在试验研究时,相对误差要求严格取D=0.1,在大田调查时相对误差可放宽到D=0.2或0.3,确定出所需最适抽样株数。用序贯抽样表进行抽样时,当调查的株数,累计若虫数超过上限时,就必须进行防治,若累计若虫数小于下限时,则不需要进行防治;累计若虫数在上限和下限之间时,应继续增加抽样株数。当不易做出判断时,应需确定最大抽样数目。Gerrard等的零频率回归模型,被广泛应用于一些体小的有害生物(如蚜虫、木虱、螨类等)种群密度的估计[11];在应用时首先需满足理论抽样数以保证抽样的精度,在调查过程中不需要检查所抽取样本的虫口密度,只需记录有虫样数和无虫样数,根据建立的零频率模型,即可估计该环境寄主上的虫口密度;用零频率法估计昆虫田间种群密度,由于避免了直接计数的烦琐过程,因而具有操作简便和效率高的优点[12]。因此,在保证一定的虫情调查准确度情况下,利用合理简便的抽样设计方案进行调查就可取得较准确的虫情资料,为斑膜合垫盲蝽制定有效的防治措施提供参考依据。 致谢:承蒙南开大学刘国卿教授鉴定斑膜合垫盲蝽种名并提供相关文献资料;中国农业大学彩万志教授和本站张山林站长帮助写作,特此致谢。 [1] Josifov M.Drei neue Orthylus-Arten aus Korea (Heteroptera, Miridae). Reichenbachia, 1976, 16(11):143- 146. [2] Liu G Q.A study on systematics of the subfamily orthotylinae from China. Tianjin: Nankai University, 1998. [3] Ding Y Q.Principle and Application of Insect Mathematical Population Ecology. Beijing: Science Press, 1980, 84- 124. [4] Xu R M. Population Ecology of Insect., Beijing Normal University Press, 1988, 8- 60. [5] Taylor L R.Aggregation,variance and the mean. Nature, 1961, 189:732- 735. [6] Iwao S, E Kuno.An approach to the analysis of aggregation pattern in biological populations//Patil G P, Pielou E C,Waters W E. Statistical Ecology. The Pennsylvania State University Press, Pennsylvania, 1971,1:461- 513. [7] Waters W E.A quantitative measure of aggregation in insects. Journal of Economic Entomology, 1959, 52:1180- 1184. [8] Bliss C I, Owen A R G.Negative binomial distributions with a common K. Biometrika, 1958, 45:37- 58. [9] Gerrard D J, H C Chiang.Density estimation of com rootworm egg populations based upon frequency of occurrence.Ecology,1970, 51 (2):237- 245. [10] Ding Y Q. Mathematical Ecology of Insects.Beijing. Beijing: Science Press, 1994,126- 134. [11] Wang X G,Liu S S.Development of binomial sampling models for predicting insect population density. Journal of Biomathematics,1996, 11(3):45- 51. [12] Cai D C,Li W,Xiao D M.Estimation of the larval population density of Liriomyza sativae on tomato leaves by zero frequency method.Plant Protection, 2011, 37(2):159- 161. 参考文献: [2] 刘国卿.中国合垫盲蝽亚科系统学研究.天津:南开大学, 1998. [3] 丁岩钦.昆虫种群数学生态学原理与应用.北京:科学出版社, 1980, 84- 124. [4] 徐汝梅.昆虫种群生态学.北京:北京师范大学出版社, 1988, 8- 60. [10] 丁岩钦.昆虫数学生态学.北京:科学出版社, 1994, 126- 134. [11] 汪信庚,刘树生.昆虫种群密度的二项抽样估计模型研究进展.生物数学学报,1996, 11(3):45- 51. [12] 蔡笃程,李炜,肖冬梅.番茄叶片上美洲斑潜蝇幼虫种群密度的零频率估计法.植物保护,2011, 37(2):159- 161. Spatial distribution pattern and sampling technique forOrthotylus(O.)sophoraenymphs onSophorajaponica ZHU Huiying1, SHEN Ping1,*,WU Jianhua2, WANG Xindong1, CHANG Chengxiu1,TIAN Wei1 1StationofForestPestManagementandQuarantineofLinxiaHuiNationalityAutonomousRegion,GansuProvince,Linxia731100,China2AgriculturalSchoolofLinxiaHuiNationalityAutonomousRegion,GansuProvince,Linxia731100,China Orthotylussophoraehas become a serious pest forSophorajaponicain Linxia Prefecture of Gansu Province in recent years. The spatial distribution pattern ofO.sophoraenymphs inS.japonicagarden was determined by six spatial distribution pattern indices, and the assembling reasons were analyzed using Taylor′s regression model (1961) and lwao′s regression equation (1971). The results indicated that the aggregated distribution ofO.sophoraenymphs in the field fits the negative binomial series (kc=0.6169).Thereasonfortheaggregationmaybeduetosomeenvironmentalfactors.Onthebasisofthedistributionpattern,theoptimalsamplingnumberandsequentialsamplingtablewerecalculatedusinglwao′smethod.ThezerofrequencymodelforthemeandensityestimationofO.sophoraenymphs was established on the basis of Gerrard′s method (1970) as follows:x=1.7457(-lnPo)1.1119. Orthotylus(O.)sophorae;spatial distribution pattern;sampling technique 甘肃省临夏州科技计划资助项目(2011-N-S- 11) 2012- 09- 23; 2013- 03- 15 10.5846/stxb201209231341 *通讯作者Corresponding author.E-mail: lx-sp@sohu.com 朱惠英,沈平, 吴建华,王新东,常承秀, 田炜.斑膜合垫盲蝽若虫在国槐上的空间分布型及抽样技术.生态学报,2014,34(4):832- 836. Zhu H Y, Shen P,Wu J H, Wang X D, Chang C X,Tian W.Spatial distribution pattern and sampling technique forOrthotylus(O.)sophoraenymphs onSophorajaponica.Acta Ecologica Sinica,2014,34(4):832- 836.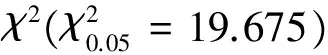

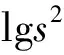
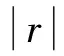


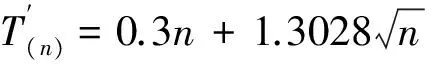
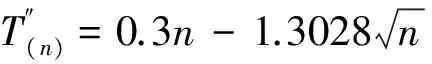
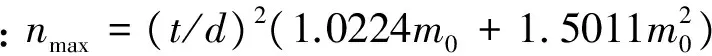


3 讨论
