某中心开孔加筋扁球壳稳定性设计

邵 同 平

(中冶南方工程技术有限公司技术研究院，湖北 武汉 430223)

某中心开孔加筋扁球壳稳定性设计

邵 同 平

(中冶南方工程技术有限公司技术研究院，湖北 武汉 430223)

利用ANSYS软件进行了均布荷载下中心开孔加筋扁球壳的荷载—位移全过程分析，得到稳定极限承载力，并按稳定理论修正公式计算了该结构的局部稳定承载力，通过等稳条件，最终确定了该加筋扁球壳的稳定性容许承载力并进而求出了稳定系数K。

加筋扁球壳，非线性屈曲，有限元分析

0 引言

随着近代工程技术的发展，薄壳非线性稳定问题的研究越来越引人注目，求解它的精确解在数学上存在很大困难，通常解决的问题范围较窄。多年来，人们大都采用某种近似方法来求解结构较简单的扁球壳稳定性问题，而对于结构较复杂的开孔扁球壳的研究比较少。刘人怀[1]、Tillman[2]和康盛亮[3]等人先后利用修正迭代等方法研究了开孔扁球光壳的非线性稳定问题，获得了一些有益的结果。但对于几何参数较大的开孔加筋扁球壳的非线性稳定问题基本上未见相关文献。

本文将利用ANSYS软件，按考虑几何非线性的有限元方法计算稳定极限承载力，并结合局部、整体屈曲的稳定关系条件，得出此问题的稳定容许承载力和稳定系数并指导设计。

1 中心开孔加筋扁球壳结构形式

某新型煤气柜的柜顶结构，是典型的具有硬中心的开孔加筋扁球壳结构(见图1)。它的环向加筋肋梁有10圈，径向加筋肋梁有32根，径向加筋肋梁的外端支承在气柜的立柱上，里端支承在开孔处的刚性中央环梁上，加筋肋梁上铺设钢板。为了保证壳体与加筋肋梁共同工作，径、环向加筋肋以及加筋肋与钢板壳体之间的连接一律用满焊连接，同时，由于加筋肋之间板格单元的尺寸过大，还在各个板格单元上又设置了角钢加筋肋，以加强板格单元的局部屈曲承载能力。该结构按加筋薄壁壳结构理论设计，能充分利用材料的性能，具有轻质、大跨度、承载力大的特点，属于稳定性敏感结构，因此，进行稳定分析特别重要。

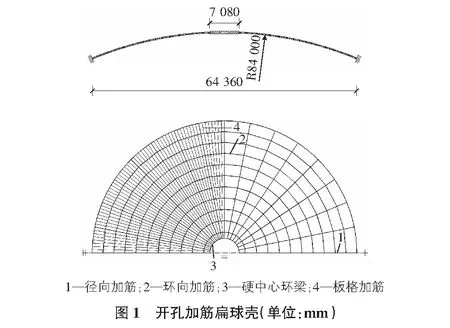
2 中心开孔加筋扁球壳整体稳定极限承载力

通过利用大型通用有限元软件ANSYS建模计算。建模时采用自底向上的方式建立几何模型，加筋肋梁用空间梁单元Beam188模拟，钢板壳用壳单元Shell181模拟，这两个单元的节点自由度完全匹配，且非常适合分析非线性问题。有限元模型如图2所示。

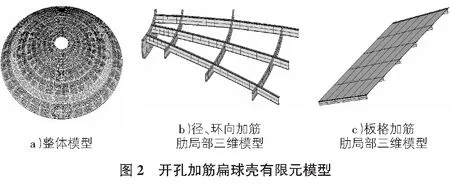
根据文献[4]的研究结果，如果加筋壳其壳体的加工质量不佳，一般来说，壳的稳定承载力将要大幅下降，幅度大概在1/2～1/3之间。因此，必须考虑扁球壳的几何缺陷。在该结构进行非线性屈曲分析时，采用它的第一阶特征值屈曲模态作为初始缺陷分布模态。

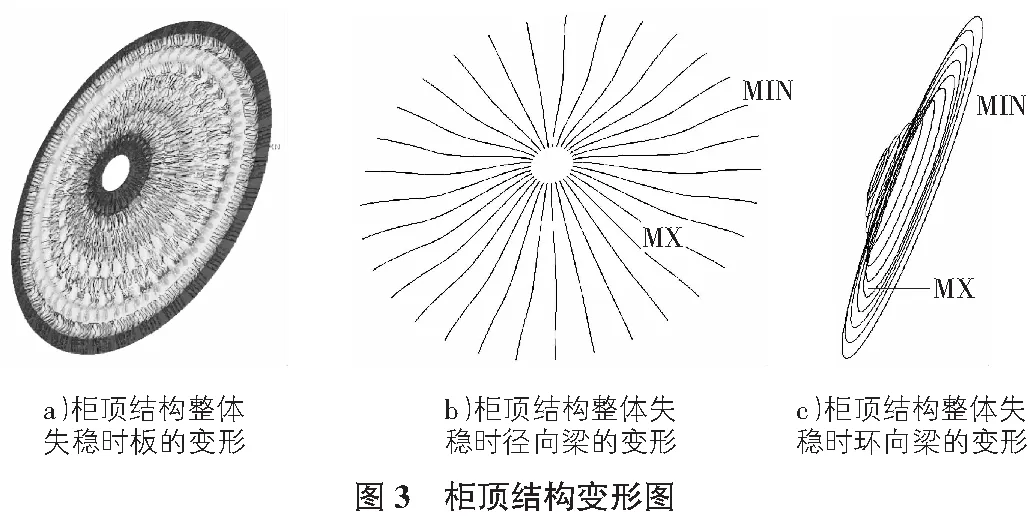
按上述计算假设，首先进行柜顶结构的特征值屈曲分析以提取第一阶屈曲模态，在考虑初始缺陷后，利用弧长法进行非线性求解，迭代求解结束时，绘制结构的挠度位移变化，见图3。在加载过程中，柜顶结构从外向内的第4圈板壳首先出现局部屈曲，继续加载时，扁壳从外向内逐渐出现位移。最后当荷载达到屈曲临界荷载时，在中环梁与边环梁距离的中部附近，位移最大，结构整体失稳。柜顶结构的整体失稳的屈曲模态为明显的反对称屈曲模态。

在径、环向加筋肋梁和壳板上选取位移最大的节点进行研究，得到相应的荷载—位移全过程曲线，综合考虑模型假设带来的误差后，稳定极限承载力折减为15.7 kN/m2。

3 中心开孔加筋扁球壳局部稳定承载力

柜顶加筋壳板的局部稳定承载力按稳定理论分析并且进行必要的修正，在这里主要是计算无加筋曲板和有加筋曲板的稳定问题，具体如下述。

3.1 曲板的压缩屈曲

3.2 带有中心纵向加筋条简支曲板的压缩屈曲

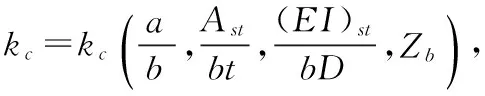
需要注意的是，对于曲板元件，按小挠度线性理论分析得到的屈曲荷载与试验数据很不一致，其差异程度取决于曲板元件的几何参数和荷载形式。对于受压曲板，根据其曲率参数的大小，屈曲特性类似于在圆筒至平板间变化。对于有中等或大的曲率参数曲板，压缩屈曲应力试验值比理论值低的多。这种差异同样存在于加筋曲板中，所以，在缺少加筋曲板试验值的情况下，必须对加筋曲板的理论值进行适当的修正。

确定加筋曲板压缩屈曲应力的修正方法如下：1)首先确定加筋曲板压缩屈曲系数的理论值kc(r)；2)确定具有相同Zb和R/t无加筋曲板的压缩屈曲系数理论值kc(0)；3)计算差值Δkc=kc(r)-kc(0)及Δσcr；4)计算无加筋曲板的压缩屈曲应力，这里当板宽>板长，按筒计算；板宽<板长，按曲板计算；5)计算相应平板的压缩屈曲应力；6)取4)与5)中大的应力加到Δσcr中，其和即为修正的加筋曲板压缩屈曲应力。

3.3 柜顶板的局部稳定承载力计算

由于最外圈板边的边界条件改变以及此部位曲板的加筋条的间距变大，不难判断得出，最外圈板的局部稳定承载力在所有板格中将是最小的，其局部稳定承载力计算参数如下：b=792 mm(加筋条间距)，a=2 800 mm(曲板长度)，Ast=940 mm2(加筋条截面∠80×6)，t=4 mm(面板厚度)，R=84 000 mm(曲板曲率半径)，E=206×103N/mm2，I=57.2×104mm4(加筋条惯性矩)。

在按3.2节步骤5)计算相应加筋平板的屈曲应力时发现，此加筋平板在纵向压缩荷载作用下不会发生总体屈曲，亦即只发生薄板局部屈曲。按3.2节计算的加筋曲板的压缩屈曲应力最终结果为：σcr=23.7 MPa。

4 中心开孔加筋扁球壳整体稳定设计

通常，对于钢结构(平板、曲板)设计，有两种考虑方法。一种是不允许板件的屈曲先于构件的整体屈曲。另一种就是允许板件的屈曲先于整体屈曲。虽然板件的屈曲会降低构件的承载能力，但通过利用板件的屈曲后强度，整个结构并未整体失稳，从节省钢材来说反而合算[6,7]。对于网格加筋球壳，由几个壳(内表面布肋或外表面布肋)所进行的校核试验表明，个别网格的局部失稳对总体失稳的影响不大[4]。

对于薄壁加筋板壳，理论分析和实验研究都表明[8，9]，局部屈曲和整体屈曲往往具有耦合波型，局部屈曲的波型可促进整体屈曲，整体屈曲的波型也可促进局部屈曲，无论哪种屈曲波型在先，都可发生相互影响，而两种波型同时出现时，影响更为严重，这种相互影响使得这种结构对原始缺陷相当敏感，从而大大降低了屈曲承载能力。如果不考虑波型耦合的非线性屈曲，这种结构的设计就会出现危险。

基于上述分析，按文献[10]研究结果并结合实际建设经验，在设计柜顶结构时，采用局部屈曲荷载略大于整体屈曲荷载进行设计是合理的。经试算，按整体稳定应力控制时对应于施加在柜顶的均布荷载为[qu]=1.88 kN/mm2，此均布荷载亦即整体稳定容许承载力，它对应的稳定系数为K=15.7/1.88≈8。此稳定系数明显大于参考文献[11]之值，它反映了由于薄壁加筋壳结构相应于网壳结构，有更难控制的加工安装误差、焊接残余应力和变形等，同时在结构有初始缺陷时，对于稳定更加敏感，所以，它的整体稳定系数比网壳结构的大是基本合理的。

5 结语

工程上大尺寸的中心开孔加筋扁球壳的稳定性设计是相当困难的问题，至今未见有相关的深入探讨。通过本文的研究，得到了该类工程稳定设计的下述结论：

1)探讨了该类结构稳定性设计的方法，即首先进行非线性有限元分析以得到结构的整体稳定极限承载力，然后进行其局部稳定承载力计算，最后按局部、整体稳定的关系确定其整体稳定容许承载力。

2)应考虑局部屈曲和整体屈曲波型耦合作用，此时，采用局部屈曲荷载略大于整体屈曲荷载的原则进行稳定承载力的设计。

3)稳定系数可按K=8取值，亦即在求得结构的稳定极限承载力后，用它除以稳定系数即可得到整体稳定容许承载力。

[1] 刘人怀.均布载荷作用下开孔扁球壳的非线性稳定问题[J].应用数学和力学,1988,9(3)：205-217.

[2] Tillman,S.C..On the buckling behavior of shallow spherical caps under a uniform pressure load[J].International Journal of Solids and Structures,1970,6(1):37-45.

[3] 康盛亮.大几何参数的开孔扁球壳的非线性稳定问题的奇摄动解法[J].同济大学学报,1990,18(4)：477-486.

[4] B.T.利津,B.A.皮亚特金.薄壁结构设计[M].北京:国防工业出版社,1983:138-154.

[5] 崔德刚.结构稳定性设计手册[M].北京:航空工业出版社,2006:64-66.

[6] 陈绍蕃.钢结构[M].北京:中国建筑业出版社,1994:115-116.

[7] 唐家祥,王仕统,裴若娟.结构稳定理论[M].北京:中国铁道出版社,1989:313-321.

[8] Svensson,S.E.,Croll,G,J.A..Interaction between local and overall buckling[J].Int.J.Mech.Sci,1975(17)：307-321.

[9] Croll,J.G.A..Model of Interactive buckling of stiffened plates[J].J.Enging.Mech.D.,Proc.ASCE,1975,101(5)：575-591.

[10] 中国科学院力学研究所固体力学研究室板壳组.加筋圆柱曲板与圆柱壳[M].北京:科学出版社,1983:260-285.

[11] JGJ 61-2003,网壳结构技术规程[S].

On the stability design of a truncated stiffened shallow spherical shells

SHAO Tong-ping

(Technology Research Dept.of WISDRI Engineer & Research Incorporation Limited， Wuhan 430223, China)

By using ANSYS, the load-displacement whole-process analysis has been carried out, and the ultimate bearing capacity is gotten, the capacity of local stability of the structure is calculated with stability theory. The stability of the allowable bearing capacity and factorKare determined finally by the connection between the local and overall stability.

truncated stiffened shallow spherical shell， nonlinear buckling， finite element analysis

1009-6825(2014)36-0022-03

2014-10-18

邵同平(1972- )，男，高级工程师

TU378.7

A