基于模糊PID控制的同步电动机功率因数调节*

谢慕君， 肖婷婷， 步伟明

(长春工业大学 电气与电子工程学院，吉林 长春 130012)

0 引 言

在工业生产中广泛使用的变压器、异步电动机等属于感性负载，都需要从电网中吸收滞后的无功负荷，降低了电网的功率因数，使电机和供电设备不能充分利用。常用的感性无功补偿方法有并联静态电容器、同步调相机及同步电动机过励运行等。其中采用同步电动机过励运行方法最为经济、简单。因此，在有同步电动机运行的场合，可通过调节同步电动机励磁装置励磁电流，使同步电动机工作在过励状态，充分发挥同步电动机的无功补偿能力，提高电网的功率因数[1]。

常规PID控制是固定增益的控制器，不具有在线调整参数的功能，故参数整定有一定的困难，影响其控制效果。近年来，模糊控制方法在解决复杂、时变及没有精确的数学模型方面有着自身的优越性[2-3]。把两者优点结合起来的模糊PID参数自整定控制对同步电动机功率因数的调节会起到更好的控制效果。

为实现对同步电动机功率因数的有效调节,本文设计一种基于模糊PID参数自整定的恒功率因数闭环控制系统。在控制系统中，励磁电流调节为内环，主要作用是保持励磁电流的稳定性和励磁电流调节的快速性。功率因数调节为外环，采用模糊PID参数自整定控制，其优点是使电机在运行过程中当负载突变、电网电压变化及电机参数变化时，始终保持功率因数恒定。

1 同步电动机功率因数调节原理

由同步电动机的“V”形曲线可知，当从某一欠励状态开始增加励磁电流时，电动机输出的超前无功功率开始减少，电枢电流中的无功分量也开始减少；达到正常励磁状态时，无功功率变为零，电枢电流中的无功分量也变为零，此时，如果继续增加励磁电流，电动机将输出滞后性的无功功率，电枢电流中的无功分量又开始增加[4-5]。故可通过调节励磁电流改变同步电动机的功率因数。图1为同步电动机的“V”形曲线。

图1 同步电动机的“V”形曲线

本文采用恒功率因数控制方法，即通过调节励磁电流使同步电动机的功率因数维持在近似为1的过励磁情况下，以使同步电动机发挥出最大的功效。

2 同步电动机功率因数调节控制算法

本文设计的模糊PID参数自整定控制器的输入语言变量为功率因数角的偏差e及偏差变化率ec，输出语言变量为PID控制器的三个参数Kp、Ki、Kd，这样就确定了一个双输入三输出的模糊控制器。

在本文中，模糊决策采用Mamdani型算法[6]。输入变量误差e、误差变化率ec及输出变量的基本模糊集都取7个变量{NB,NM,NS,ZO,PS,PM,PB}，并设e的模糊子集的论域为{-n,-n+1,…,0,…,n-1,n}；ec的模糊子集的论域为{-m,-m+1,…,0,…,m-1,m}；Kp,Ki,Kd模糊子集的论域为{-1,-1+1,…,0,…,1-1,1}。一般选误差论域的n≥6，误差变化论域的m≥6，控制量的论域l≥7。本文中选择各语言变量的模糊子集的论域皆为{-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7}，转换算式为

(1)

式中，a表示低限值，b表示高限值，n=7，k表示量化因子。通过式(1)，将在不同基本论域上的各模糊变量都转换到[-7，7]上。本文采用三角形隶属度函数及Zadeh推理，解模糊采用重心法[7]。PID参数的整定必须考虑到不同时刻3个参数的作用及相互之间的关系。模糊PID参数自整定是在PID算法的基础上，通过计算当前系统误差e和误差变化率ec，利用模糊规则进行模糊推理，查询模糊规则表进行参数调整。模糊控制设计的核心是建立合适的模糊规则表，得到针对Kp、Ki、Kd各参数分别整定的模糊控制规则，如表1所示。

3 仿真试验研究

同步电动机功率因数调节控制系统的结构框图如图2所示。

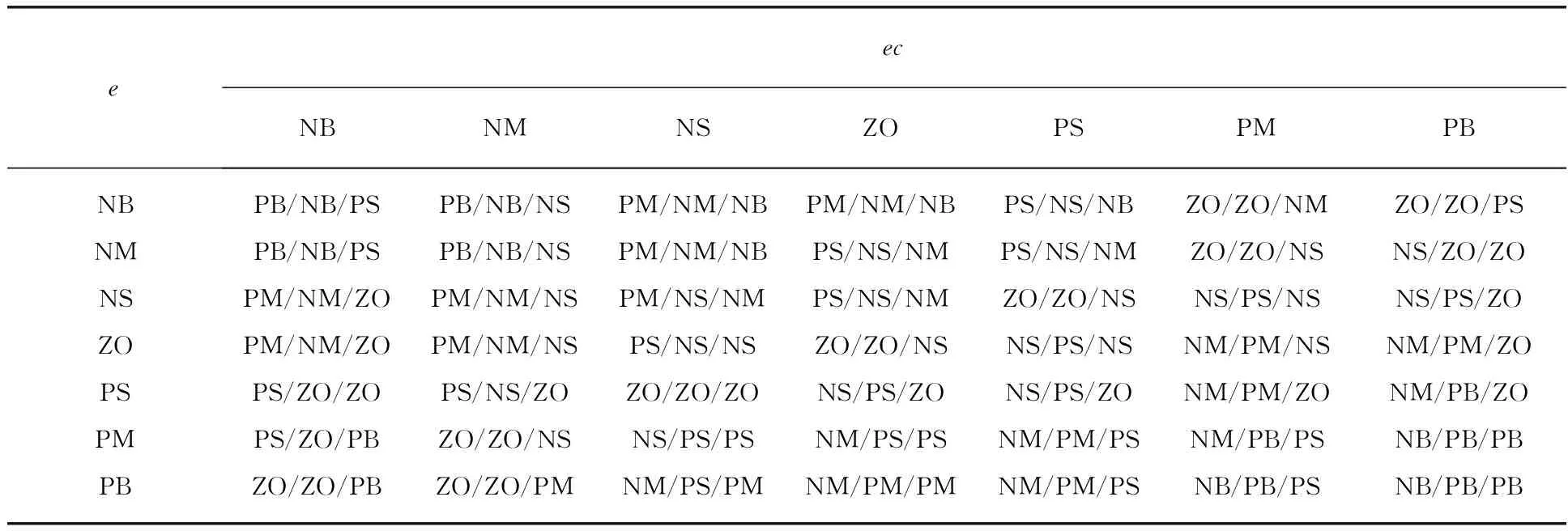
表1 Kp、Ki、Kd的模糊控制规则表

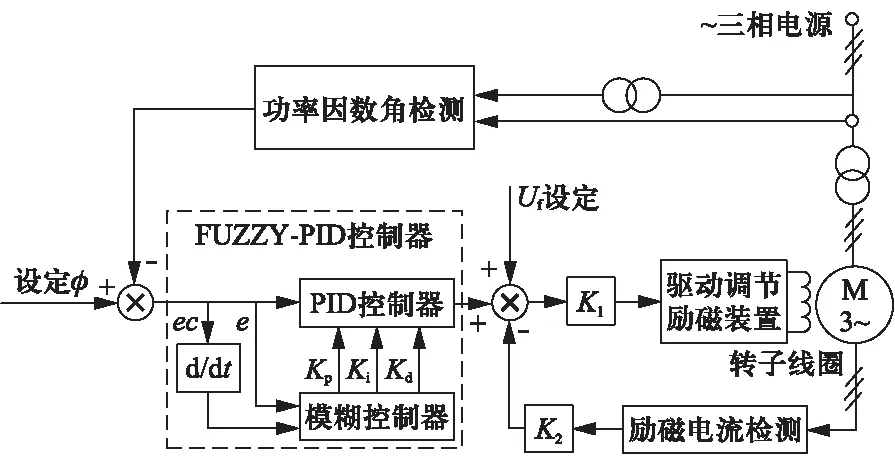
图2 同步电机恒功率因数控制系统的结构框图

针对控制系统框图，采用MATLAB的Simulink建立同步电机恒功率因数控制系统仿真模型，如图3所示。其中，FUZZY-PID模块是模糊PID参数自整定控制器，如图4所示；subsystem模块是励磁电流调节模块，如图5所示,他是以直流电压为控制信号，通过一个幅值和频率可变的三角载波，两者进行比较，以其交点处产生脉冲的前后沿形成PWM波，通过控制PWM的占空比来控制IGBT的通断，改变励磁电流的值，从而实现功率因数的闭环控制。

图3 同步电机恒功率因数控制系统Simulink仿真模型

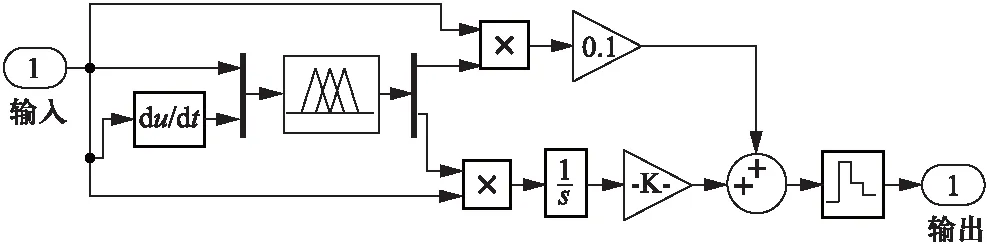
图4 FUZZY-PID模块内部模型图

图5 励磁调节subsystem模块内部模型图

本文设计的模糊PID参数自整定控制器的输入变量、输出变量选取的基本论域分别为误差e： [-40°，40°]；误差变化率ec： [-400°/s，400°/s]；比例系数Kp： [-2，2]；积分系数Ki： [-0.3，0.3]；微分系数Kd： [-0.06，0.06]。

同步电动机模块的各个参数如下： 视在功率Pn=112kW，线电压Un=440V，频率fn=50Hz，定子阻抗Rs=0.26Ω，定子漏感L=1.14mH，磁场阻抗Rf=0.13Ω，磁场电感L=2.1mH，d轴、q轴的感抗Lmd、Lmq分别为13.7mH、11.0mH，d轴、q轴的阻抗Rkd、Rkq分别为0.0224Ω、0.02Ω，d轴、q轴的漏感Llkd、Llkq分别为1.6mH、1.2mH，转动惯量系数J=24.9kg·m2，摩擦系数F=0，极对数P=2。PWM模块不选择内部信号，载波频率为1080Hz。

本文同步电动机的功率因数角设定值为0°，分别对PID控制和模糊PID参数自整定控制在负载突变、电网电压变化及电机参数变化三个方面进行仿真，仿真结果如图6所示。

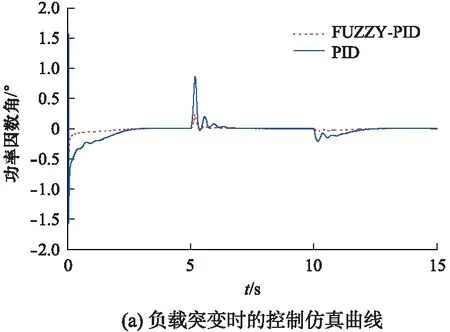
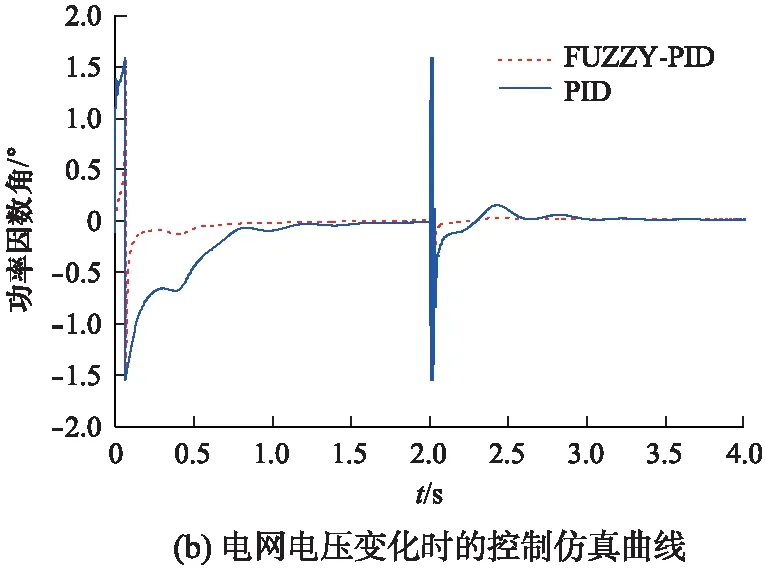
图6 恒功率因数控制系统仿真曲线

(1) 负载突变时的特性比较。在t=5s时刻，负载突然从100kW变为50kW,在t=10s时刻，负载再从50kW突变为100kW时的仿真曲线如图6(a)所示。

(2) 电网电压变化的响应特性比较。在t=2～ 2.1s时间内，电网电压发生变化时的仿真曲线如图6(b)所示。

(3) 电机参数变化的响应特性比较。电机参数变化： 电机的定子绕组从0.26Ω变到0.30Ω；转子绕组电阻从0.13Ω变到 0.15Ω；转动惯量从24.9kg·m2变到27.0kg·m2。

电机参数变化前、参数变化后的仿真曲线分别如图6(c)、图6(d)所示。

由常规PID控制器和模糊PID参数自整定控制器仿真曲线可知： 模糊PID参数自整定控制系统能很快地跟踪给定值，响应较快，误差小。从图6(a)可知当负载突变时，模糊PID参数自整定控制在达到稳态误差时的调节时间相对较少，且偏离原来稳定值的程度小于0.5°；从图6(b)可知当电压变化时，模糊PID参数自整定控制在干扰过后恢复到稳态误差时的调节时间比常规PID明显减少；通过图6(c)、图6(d)对比可知： 在电机模型参数变化前后，模糊PID参数自整定控制的仿真曲线无明显变化，而常规PID变化明显，上升速度变慢，调节时间变长。可见模糊控制比一般的PID控制控制性能优越，仿真曲线的具体数据对比见表2。

4 结 语

本文设计的基于模糊PID参数自整定控制器的恒功率因数闭环控制系统，保证了同步电动机功率因数调节的精度。采用MATLAB软件对设计的控制系统进行仿真试验，结果表明所设计控制系统能有效克服电机参数变化、负载扰动等因素的影响，具有更快的响应速度、更高的稳态精度和更强的鲁棒性。

表2 仿真曲线的性能指标对比数据表

【参考文献】

[1] 李崇坚.交流同步电机调速系统[M].北京： 科学工业出版社,2007.

[2] XU H Y, WANG C. Power factor improvement in industrial facilities using fuzzy logic excitation control of synchronous motor [J〗. IEEE Computational Intelligence and Software Engineering, 2009(2)： 1418-1421.

[3] 姜全录,吴军,郝英军.基于工厂供配电系统功率因数的研究[J].赤峰学院学报(自然科学版),2012(6)： 163-164.

[4] 陈成功,史伟伟,李金华.小型独立系统中同步发电机的数字仿真[J].电机与控制应用,2011,38(5)： 1-3.

[5] ABHISEK U, RICHARD B, ANDREA A. Estimation of induction motor operating power factor from measured current and manufacturer data [J]. IEEE Transactions on Energy Conversion, 2011(6)： 699-700.

[6] 宋佳,王利强.利用DSP实现同步电动机功率因数闭环调节[J].河北工业科技,2010,27(6)： 486-488.

[7] 李春林.同步电机稳定性能仿真分析[J].电机与控制应用,2008,35(6)： 11-13.