基于伪降阶磁链观测器的速度辨识方法
2014-08-08吴晓新张笠君
柳 巍, 阮 毅, 吴晓新, 张笠君
(上海大学 机电工程与自动化学院,上海 200072)
0 引 言
磁场定向控制的概念被广泛应用于高性能感应电机控制。在感应电机驱动系统中,为了获得速度信息,需要一个速度传感器,如测速发电机、旋转变压器、数字位置编码器等。在交流传动领域,已提出基于磁场定向的无速度传感器方案,主要通过软件算法代替硬件得到电机速度[1- 4]。
文献[3]和文献[4]提出了一种自适应全阶磁链观测器方案,用于估计转子磁通和电机速度。速度自适应率主要是采用Popov和Lyapunov稳定性方法来实现。由于全阶磁链观测器的反馈增益矩阵与电机的运行速度有关,实现比较复杂。如果采用开环的全阶磁链观测器,即增益矩阵设置为零,则电机在低速情况下会出现不稳定的现象,在重载情况下会出现较大的速度误差[5]。文献[5]提出了一种基于自适应伪降阶磁链观测器的速度辨识方法,利用Lyapunov方法进行速度辨识,在中、高速范围,伪降阶磁链观测器的性能相比全阶磁链观测器有了一定的改善。Lyapunov方法需要确定适当的Lyapunov函数,该函数的确定非常困难。文献[6]利用Popov方法代替Lyapunov方法用于速度辨识。由于文献[5]和文献[6]都是在观测磁链和实际磁链相等的假设条件下,得到观测器的极点与电机转速无关,所以系统的稳定性还有待进一步研究。
本文研究了一种自适应伪降阶磁链观测器,反馈增益矩阵设计简单,与电机转速无关。比常见的全阶磁链观测器简单,因此需要的计算时间更少,有利于数字实现。对该方法进行了仿真和试验验证,从低速到高速范围,电机都能稳定运行,克服了低速不稳定的问题,证明了该方法的有效性。
1 异步电机及伪降阶观测器模型
在两相静止坐标系,将定子电流和转子磁链作为状态变量,则异步电机模型的状态方程可表示为
(1)
(2)
式中:ωr——转速;
τr——转子时间常数;
Lm——互感;
Ls、Lr——定、转子电感;
σ——漏感系数;

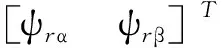

将定子电流观测误差ei作为反馈量,则伪降阶自适应观测器如图1所示。ei通过误差反馈增益矩阵G构成渐进状态观测器,并通过自适应机制对转速进行估计。以is和ψr为状态变量构建的异步电机伪降阶闭环观测器可表示为
(3)
(4)
式中: G——反馈增益矩阵,G的值为了确保观测器的稳定性。

图1 伪降阶自适应观测器
2 速度辨识及反馈矩阵设计
2.1 速度辨识
式(3)和式(4)中,如果将转速认为是变化的参数,将电机模型减去观测器模型,可以得到静止坐标系下的状态观测误差方程

(5)

根据式(5),误差方程可以等价为非线性反馈系统。该系统由一个线性定常前向通道和一个非线性时变反馈通道组成,状态观测误差框图如图2所示。
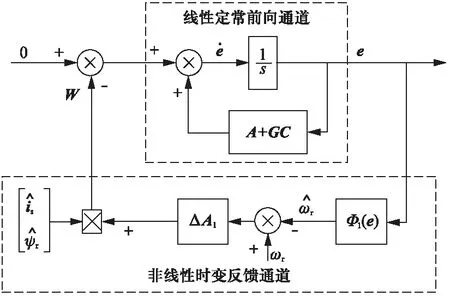
图2 状态观测误差框图
图2中,Φ1(e)是转子转速的自适应辨识函数。根据Popov超稳定性理论,一个由线性前向通道和一个非线性时变反馈通道组成的系统,如果其非线性反馈部分满足Popov不等式,那么该系统处于渐进稳定的充分必要条件是线性前向通道的传递函数严格正实。假设图2中线性定常前向通道为严格正实,只要选取适当的自适应律,使非线性反馈部分满足Popov不等式(6),即可保证系统渐进稳定。
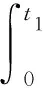
(6)
文献[4]给出了详细证明,如果电机转速辨识满足式(7),则满足Popov不等式。

(7)
式中:Kp、Ki——比例、积分系数。
2.2 反馈矩阵设计
PI自适应律可以保证非线性反馈部分满足Popov不等式,则该转速估算系统的稳定性只由线性前向通道的传递函数G(s)的严格正实性决定。首先求出前向通道传递函数矩阵G(s)的表达式,将式(5)在S域展开为
(8)

展开可得

(10)
化简,得
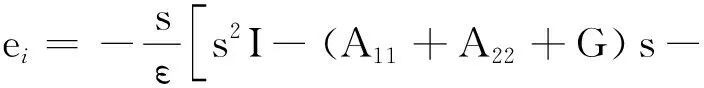
(11)


(12)
其中:
y=-g2-ωr
如果前向通道传递函数矩阵G(s)严格正实,则必须满足式(13)。
G(jω)+G*(jω)>0 ∀ω>0
(13)
其中,G*(jω)是G(jω)的共扼转置矩阵,将式(12)带入上式中可得

(14)
其中:
B(s)= ss*(s+s*)I+2ss*xI+ (s+s*)mI+(s*-s)nJ
(15)
可得当且仅当以下条件成立时,式(13)才成立。
B(s)>0
(16)
将s=jωe代入式(16),ωe为同步角频率,式(16)展开,可得
(17)
由式(17)可得保证前向通道传递函数矩阵严格正实的条件为
(18)
式(18)化简可得
(19)
将式(19)中的ωc称为临界频率,具体定义为
(20)
式(19)即为保证基于伪降阶磁链观测器转速估算系统的线性前向通道传递函数G(s)严格正实的约束条件,也即保证转速估算系统满足Popov超稳定性定理的约束条件。
由稳定约束条件式(19)和式(20)可知,临界频率与伪降阶磁链观测器的反馈增益矩阵相关,临界频率越小,则不稳定区域也会越小;若将临界频率设计为0,则可将不稳定区域收缩到最小,所以反馈矩阵的设计准则是
(22)
简化得
(23)
式(23)即为保证系统稳定的反馈增益矩阵的设计准则。根据该准则,可以将反馈矩阵设计为
(24)
由式(24)可知,反馈增益矩阵设计简单,与电机转速无关。
3 仿真验证
为验证基于伪降阶磁链观测器的转速辨识算法的有效性,在MATLAB环境下搭建了仿真模型。仿真模型中电机参数与实际电机相同,参数如下:PN=3kW,f=50Hz,IN=6.9A,n=1400r/min,Te=20N·m,Rs=1.85Ω,Rr=2.658Ω,Ls=0.2940 H,Lr=0.2898H,Lm=0.2838H,np=2。
电机正反转运行时的仿真结果如图3所示。在0s时给定转速为750r/min;1.5s时,给定转速变为-750r/min。从图3中可知,观测转速很好地跟踪实际转速,转速响应速度快,电流和磁链的跟踪性能很好,稳定后保持正弦变化。
低速时,电机带额定发电性负载的运行结果如图4所示。在1s时突加额定发电性负载,电机转速波动后又保持在100r/min,转矩电流分量响应速度快,没有出现不稳定现象,转速观测系统保持稳定。
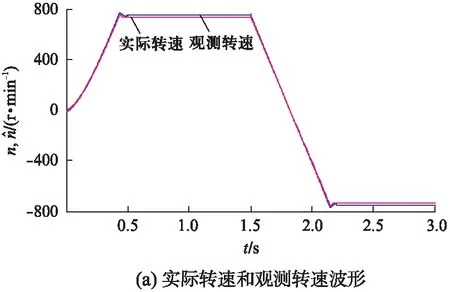

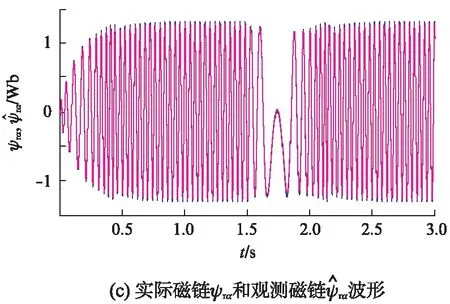
图3 正反转运行波形
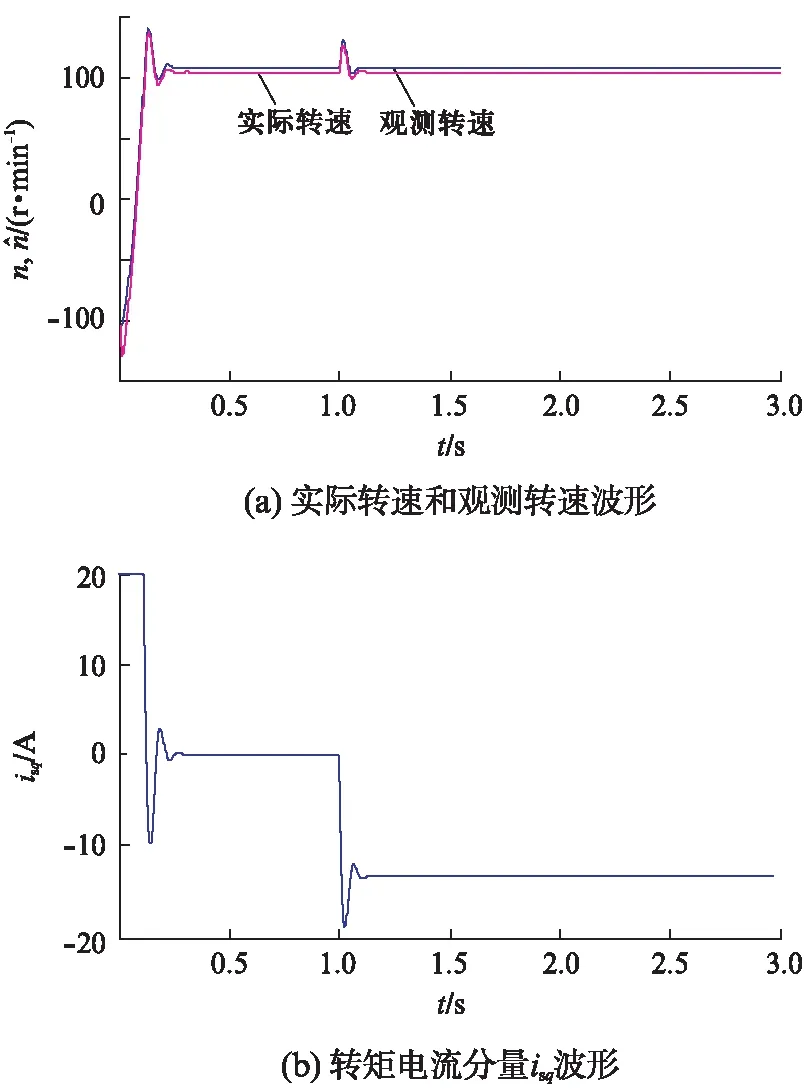
图4 100r/min时,突加额定发电性负载运行波形
4 试验结果
为了进一步验证本文提出的方法的有效性,通过试验进行了验证。主电路采用IGBT模块构成一个三相电压源逆变器,开关频率为4kHz,控制系统以dsPIC30F6010A为控制核心,采用矢量控制策略。为了比较观测性能,通过一个光电编码器来检测电机的实际转速。
电机转速给定为额定转速1400r/min时,实际电机转速和观测电机转速的波形如图5所示。电机转速给定为125r/min时,实际电机转速和观测电机转速的波形如图6所示。从图6可知,不管是在高速还是在低速,电机的转速观测值可以较好地跟踪电机实际转速,误差较小。电机转速为125r/min时的速度辨识结果如图7所示。由图7可知,对应的磁链角度变化,保持周期性变化,转子磁链α轴的分量如图8所示,稳定为正弦量,可以看出磁链观测器同样具有较好的观测性能。

图5 给定转速为1400r/min时,速度辨识结果

图6 给定转速为125r/min时,速度辨识结果
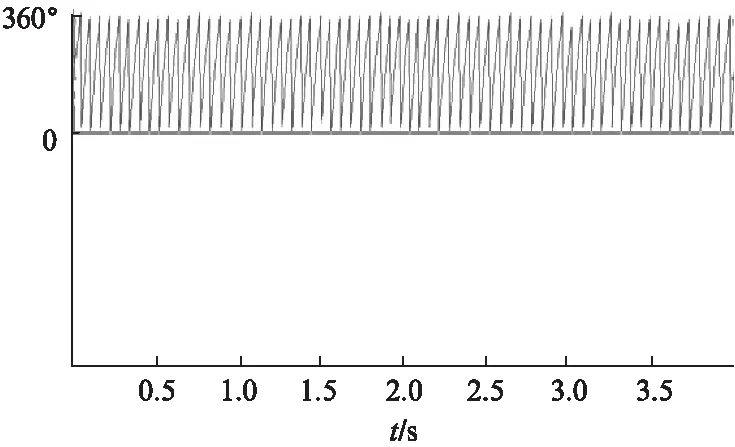
图7 磁链角度变化波形

图8 转子磁链α轴分量波形
突加突减负载时,电机的观测转速和转矩电流分量的变化波形如图9所示。电机先空载稳定运行于1400r/min,然后突然加额定负载,从图中可以看出电机转速先有略微下降,然后调节到额定转速,转矩电流分量增大并能够保持稳定,接着突然减去额定负载,转速略微上升,然后保持为额定,转矩电流分量减小到0。
电机给定转速为300r/min时,突加突减负载的试验结果,可以看出具有和额定转速时相当的性能,电机转速受负载变化的影响较小,转矩电流分量响应快。不管是在高速还是低速,系统都能保持稳定运行。
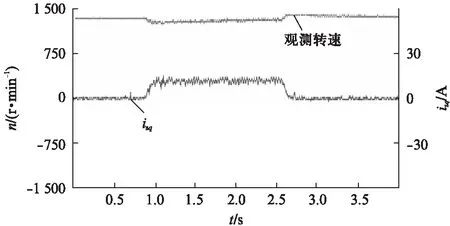
图9 给定转速为1400r/min时,负载变化试验结果

图10 给定转速为300r/min时,负载变化试验结果
5 结 语
本文提出了一种基于伪降阶磁链观测器的速度辨识方法,详细分析了该方法的基本原理,依据Popov超稳定理论设计了反馈增益矩阵,获得了满足观测器稳定性的条件,保证了电机低速运行的稳定。仿真和试验验证了该方法的可行性和实用性,从低速到高速范围,电机都能稳定运行,无不稳定现象。
【参考文献】
[1] SUWANKAWIN S, SANGWONGWANICH S . Design strategy of an adaptive full-order observer for speedsensorless inductionmotor drivestracking perfo-rmance and stabilization [J]. IEEE Trans on Industry Electronics, 2006,53(1): 96-119.
[2] 陈名辉,阮毅,宗剑,等.无速度传感器在矿用电机车矢量控制系统中的应用[J].电机与控制应用,2012,39(2): 17-20.
[3] KUBOTA H, MATSUSE K, NAKANO T. DSP based speed adaptive flux observer of induction motor. IEEE Trans Ind Applicat, 1993, 29(2): 344-348.
[4] YANG G, CHIN T H. Adaptive speed identification scheme for a vector controlled speed sensor-less inverter induction motor drive. IEEE Trans Ind Applicat, 1993, 29(4): 820-825.
[5] LIN Y N, CHEN C L. Adaptive pseudo-reduced-order flux observer for speed sensorless field oriented control of IM. IEEE Trans Ind Electron, 1999, 46(5): 1042-1045.
[6] KOJABADI H M, CHEN C L. A MRAS-based adaptive pseudoreduced-order flux observer for senso-rless induction Motor Drives. IEEE Trans on Power Electronics,2005, 20(4): 930-938.
