基于全鲁棒滑模控制的永磁同步电机伺服系统矢量控制*
2014-08-08杨代利张宏立
杨代利, 张宏立
(新疆大学 电气工程学院,新疆 乌鲁木齐 830047)
0 引 言
永磁同步电机(Permanent Magnet Synchro-nous Motor, PMSM)具有高效率、低转矩脉动、高动态性能和高能量密度等特点,现广泛应用于大范围的调速和定位系统中(如机械加工设备、机器人、电动驱动装置等),尤其适合于高精度、高性能应用的场合。但是,PMSM是一个多变量、强耦合、非线性、变参数的复杂对象。高性能的伺服控制系统要求具备响应快、无超调、抗干扰及调速精度高等特性。对于模型不确定、参数摄动和不确定的外部干扰,鲁棒性是衡量控制系统响应参考输入的重要指标[1]。常规的PID控制系统鲁棒性不够理想,很难得到比较满意的结果,而滑模变结构控制(Sliding Mode Control, SMC)具有较强的鲁棒性,且结构简单、响应快速,在PMSM的伺服系统得到了广泛应用。文献[2]将一种新的变积分切换增益的全局滑模控制策略应用于PMSM的矢量控制中,既解决了传统滑模控制中的趋近模态不具有鲁棒性的缺点,又可解决滑模控制中的抖振问题。文献[3]针对不确定性定常系统,设计了一种基于全程滑动模态的控制律,且在控制律中加入了变因子项,改善了系统性能,消除了到达阶段,具有精度高、鲁棒性强等特性。
本文针对PI控制器自适应和鲁棒性差等缺点,提出了一种时变滑模面。该滑模面带有一个时间的指数函数,由于系统初始状态就位于滑模面上,消除了到达阶段。根据该滑模面推导了控制律。为尽可能减弱抖振,采用连续函数替代了符号函数,并将负载转矩视为干扰。所设计的全鲁棒SMC控制器进一步增强了系统抗干扰能力。最后,通过仿真表明,本文所设计的全鲁棒滑模控制器比PI控制器具有更强的鲁棒性。
1 PMSM的数学模型
在研究PMSM的数学模型时,作如下假设:
(1) 不考虑磁路饱和;
(2) 不计电动机的涡流和磁滞;
(3) 电动机具有正弦反电势,电流为对称的三相正弦波电流;
(4) 转子上不存在阻尼绕组。
PMSM矢量控制方法是在dq轴数学模型上进行的,不仅可用于分析正弦波PMSM的稳态运行性能,也可用于分析电动机的瞬态性能。采用ids=0的PMSM转子磁场定向控制,此时转矩大小与转矩电流成正比,实现了PMSM的解耦控制。在dq坐标系下PMSM的状态方程:
(1)
PMSM的转矩方程:
(2)
PMSM的运动方程:
(3)
式中:uqs、iqs——定子电压、电流的q轴分量;
R——定子绕组电阻;
L——等效d、q轴电感;
pn——极对数;
ψf——转子永磁体的磁链;
ω——转子机械角速度;
J——折算到电机轴上的总转动惯量;
B——黏滞摩擦;
TL——折算到电机轴上的总负载转矩。
2 滑模面及控制策略设计
2.1 PMSM的状态方程
式中:θ*——给定位置;
θ——实际位置。
(4)
可得状态方程为

(5)

2.2 滑模面的设计
全鲁棒滑模变结构位置控制器设计包括滑动面设计和滑模控制律设计,以及削弱抖振的方法。为使系统具有全局鲁棒性,消除到达阶段,缩短到达稳态的时间,设计时变滑模面:
s=Cx-f(t)
(6)
此时,时变滑模面必须满足如下条件:
(1)f(0)=Cx(0),即状态一开始就处于滑模面上;
(2) 当t→∞时,f(t)→0,保证所设计的时变滑模面最终能到达期望滑模面。
为了满足系统控制和时变滑模面要求,本文设计时变滑模面为
s=Cx-Cx(0)e-βt
(7)
其中,C为滑模面参数,C的选取关系到系统响应时间的长短,C过小系统响应过慢,而C过大可能出现超调。C的选取至关重要。
2.3 控制律设计和稳定性分析
考虑有扰动时,系统的状态方程:
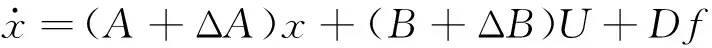
(8)
其中,ΔA,ΔB是不确定项,主要由J,B,TL参数的变化引起。负载转矩TL时常发生变化,本文将f=TL看作系统的扰动,将其包含于控制律中。

设计控制律为
Uss=-g(t)(CB)-1sgn(s)
(9)
稳定性证明[5]从略。
为了减小抖振,用函数sat(s)代替符号函数sgn(s):
(10)
式中,ε是一个小的正数,选取适当的ε,对于削弱抖振,能起到至关重要的作用。
2.4 滑模面参数C设计
滑模面的设计主要有极点配置法、二次型最优设计法、矩阵广义逆和投影变化设计法等。本文采用极点配置法来设计时变滑模面参数C。
将式(7)、式(8)改写如下:
s=c1x1+c2x2-Cx(0)e-βt=0
(11)

(12)
由此可得降阶滑动模态状态方程:
ΔB1+Df+(A22+ΔA22)Cx(0)e-βt
(13)
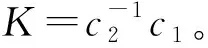
3 仿真及结果分析
为了验证上述SMC控制器,对PMSM伺服系统进行仿真,并与PID控制器进行对比。使用MATLAB/Simulink软件电气模型库SimPower-Systems搭建仿真模型,PMSM伺服系统的仿真结构图如图1所示。
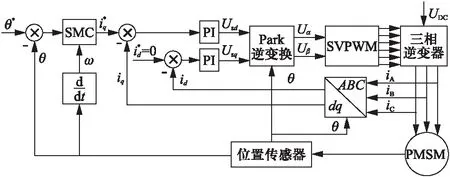
图1 PMSM伺服控制系统仿真框图
PMSM参数如下:Ld=Lq=8.5mH,Pn=4,R=2.875Ω,J=8×10-4kg·m2,Ψf=0.175Wb,B=1×10-4N·m·s。
(1) 当电机空载时,给定位置由6rad跳变到-6rad,再由-6rad跳变到50rad,最后回到0。阶跃位置响应对比曲线如图2所示。

图2 阶跃位置响应对比曲线
从图2可见,当电机空载,转矩没有变化和没有扰动以及电机本身参数不发生摄动时,全鲁棒SMC控制器响应时间较快。
(2) 给定位置θ=6rad,带负载TL=1N·m运行,在t=0.1s时,突加负载TL=4N·m,并持续时间0.03s,在t=0.2s负载变化为TL=4N·m。
从图3、图4可见,带负载运行时,全鲁棒SMC控制器稳态误差几乎为零,而PID控制器具有一定的稳态误差。在t=0.1s突加负载时,全鲁棒SMC控制器阶跃位置响应基本没有波动,而PID控制器在突加转矩时,位置明显下降。
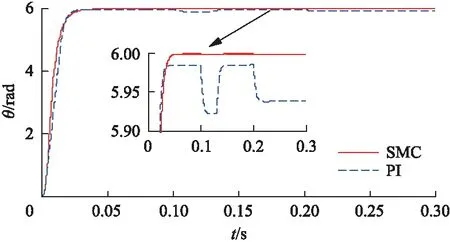
图3 带负载和有干扰以及负载变化对比曲线

图4 转速响应对比曲线
(3) 给定位置θ=6rad,带负载TL=1N·m,且电机的固有参数摄动20%。参数变化前后,SMC和PI阶跃位置响应曲线分别如图5、图6所示。

图5 参数变化前后SMC阶跃位置响应曲线

图6 参数变化前后PI阶跃位置响应曲线
图5和图6表明,全鲁棒SMC控制器在有参数摄动时,其稳态响应基本没变化。
4 结 语
本文为解决PI调节器存在的问题,依据滑模变结构理论设计了PMSM伺服系统中的位置控制器。针对电机三种工作情况进行仿真,仿真结果表明用全鲁棒滑模控制方法设计的同步电机伺服系统比PI控制器位置伺服系统具有更好的动、稳态性能,以及更强的抗干扰能力和鲁棒性。
【参考文献】
[1] FNAIECH M A, BETIN F, CAPOLINO G A, et al. Fuzzy logic and sliding-mode controls applied to six-phase induction machine with open phases[J]. IEEE Trans Ind Electron, 2010, 57(1): 354-364.
[2] 胡强辉,胡勤丰.新型全局滑模控制在永磁同步电动机中的应用[J].电机与控制应用,2010,37(2): 47-52.
[3] FENG Y, ZHENG J F, YU X H, et al. Hybrid terminal sliding mode observer design method for a permanent magnet synchronous motor control system[J]. IEEE Trans Ind Electron, 2009, 56(9): 3424-3431.
[4] 郑钰,罗继勋,旷艾喜,等.基于全程滑动模态的变结构制导律研究[J].计算机测量与控制,2011,19(12): 3012-3015.
[5] 张科,周凤歧.不确定多变量系统的全程滑态变结构控制方案设计[J].控制理论与应用,1999,16(2): 221-224.
[6] 池毓东,王岩.一种时变滑模平面的设计方法[J].上海交通大学学报,1998,32(6): 70-77.
[7] 张晓光,赵克,孙力,等.永磁同步电机滑模变结构调速系统动态品质控制[J].中国电机工程学报,2011,31(15): 47-52.
[8] 李珍国.交流电机控制基础[M].北京: 化学工业出版社,2009.
